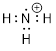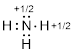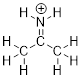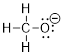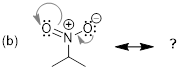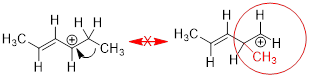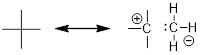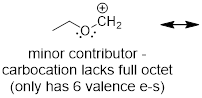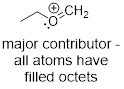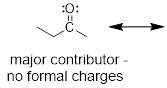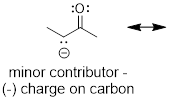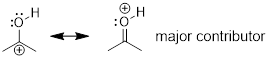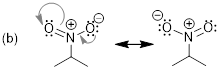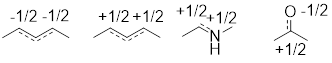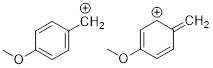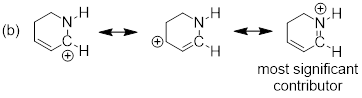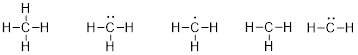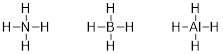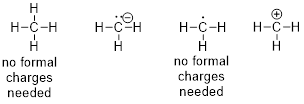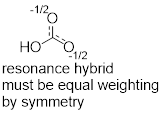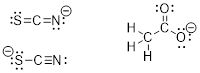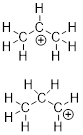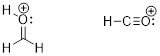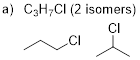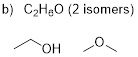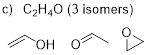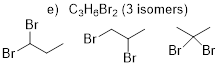The question about the definition of organic chemistry can
go on forever and indeed would change depending on the decade in which you
asked the question. Certainly, chemists would have answered the question
differently in 1920 than in 2020 – the age of LCDs, polymer processing,
industrial catalysis, modern instrumentation, and new drug discovery. We can
simplify the question by removing ‘organic’ and ask, “What is chemistry?” I
need to give a broad definition that may initially confuse you, and then I will
work to clear things up.
Chemistry studies
the ■ emergent properties
of the electromagnetic force (EM) at approximately nanometric length scales and
below (go to the link: ■ electromagnetic force; look at the table, ‘The four fundamental interactions of nature’
and take note of the row entitled, ‘Bound
states formed.’ You will see ‘atoms
and molecules’ under the column heading ‘Electromagnetic’). Take note of the other universal forces and
their bound states. This one row in the table neatly puts chemistry in terms of
scale and topic as it compares to other topics in the physical sciences. The
length scale of atoms and molecules is about 0.1 to 100 nm. For example, the sucrose
molecule, table sugar, is about 1.5 nm from end to end. Chemistry also studies emergent properties of the electromagnetic
force extrapolated to length scales that correspond to the human experience, extrapolated
from the nm-Å scale to the μm-m scale, the scale
at which humans usually build. This includes everything from the conductivity
of a copper wire to the setting time of epoxy cement.
Now I must apologize! That definition was probably too dense because
one must know quite a bit to parse it into anything sensible. Let us talk about
some broad examples of the EM force at atomic length scales. We need to spend
some time on this because the definition of chemistry will put us on the same
page.
Consider the periodic table and apply the definition of
chemistry to it. When we compare the chemical behavior of hydrogen (1H)
to one of its isotopes, deuterium (2H), they are nearly identical
even though the atomic mass is double. Likewise, the chemistries of the other
common isotopes in the periodic table are nearly identical, e.g. 12C compared to 13C.
Obviously, the force of gravitation and the property of mass do not determine
what we call chemistry! Neither does the force that sticks an extra neutron to
the nucleus to give us different isotopes determine the chemistry. The forces
between charged components (nuclei and electrons) determine the chemistry. This
is the electromagnetic force; everything chemistry derives from it.
The periodic table organizes atoms according to their
chemistries. This is the reason Li+ and Na+ have similar
chemistries. One is much heavier than the other is, but the arrangement of the
electrons with a single positive charge is similar. Both atomic species are
prone to interact with other electrons. Chemistry always focuses on the
electromagnetic force and – in particular – the energy of the electrons in the
chemical system. Logically, if we add an electron to both we get atomic Li and
Na which also have similar chemistries with some clear differences. The
chemistries of the atoms in the periodic table determine how they stick to one
another to form molecules and determine how molecules interact with each other
to determine measurable properties of gases, liquids, and solids. This
macroscopic, emergent behavior of electrons comprises a large part of
what we study in chemistry.
Light as we see it is a small portion of the ■ electromagnetic spectrum. The electromagnetic
field is a property of space. When the value is zero, space is dark. When the
value is non-zero, space gets more interesting because we can see reds to blues
with our eyes; we can detect infrared or ultraviolet with instruments; we can
detect radio signals; etc., depending on the wavelength of the EM phenomena. EM
waves interact strongly with atoms and molecules. We use this interaction to
learn about the chemistries of the material we are studying. ■ Spectroscopy is the theory and activity of
interpreting the interaction between EM radiation and atoms or molecules. Go
back to the link ■ electromagnetic force; look at the
table, ‘The four fundamental interactions of nature’ and take note of
the row entitled, ‘mediating particles.’ You will see ‘photon’
under the column heading ‘Electromagnetic’. For a charged body to repel
or attract another charged body they exchange photons. Molecules contain
charged components, which exchange photons to stay with the molecule (vs.
floating away), so the absorption of another photon changes the nature of the
association between electron and molecule (average distance changes, average
energy changes, etc.). The photon is the mediating particle of the
electromagnetic force, and chemistry relies on EM; thus, molecules interact
strongly with light.
Without spectroscopy, we would be blind to most of chemistry;
spectroscopy, therefore, is the epistemological aspect of EM that allows us to
construct theories about chemistry. To tell someone about chemistry without referencing
spectroscopy would be describing what we know without describing how we know
it. Throughout these introductory chapters we include important aspects of EM that
pertains to the chapter content.
 What is Organic Chemistry? Look at the ■ periodic table;
find atom number 6; it is the fourth atom in the second row, the carbon atom.
The C atom has diverse options to bond with itself and many other atoms. This rich
variability to make connections and to react …or not…makes life possible.
That’s right, the nature of life is chemical. Concrete aspects of life like
bone, blood and muscle are chemical, but even abstract aspects of life like
your thoughts and memories are also chemical in nature. Besides life, the
chemistry of the carbon atom is central to many other aspects of our daily
lives, such as multi-billion-dollar industries of many types. The chemistry of
the carbon atom is organic chemistry!
What is Organic Chemistry? Look at the ■ periodic table;
find atom number 6; it is the fourth atom in the second row, the carbon atom.
The C atom has diverse options to bond with itself and many other atoms. This rich
variability to make connections and to react …or not…makes life possible.
That’s right, the nature of life is chemical. Concrete aspects of life like
bone, blood and muscle are chemical, but even abstract aspects of life like
your thoughts and memories are also chemical in nature. Besides life, the
chemistry of the carbon atom is central to many other aspects of our daily
lives, such as multi-billion-dollar industries of many types. The chemistry of
the carbon atom is organic chemistry!
Most of the elements we will encounter in Chapters 1-9 of this
book are contained in the portion of the periodic table represented below.
Later we will use transition metals (e.g. Os, Cr, Zn,
Cu, Ni, Pd, Pt), but for now, let us focus on knowing the position of a subset
of elements in the periodic table. Remembering in which Group an element resides
will help you more quickly count its valence electrons and predict its
reactivity.
Exercise
1.1.1 In the empty boxes, insert the symbol for each
missing element.

1.2 BOND-LINE STRUCTURES: ELECTRONS,
BONDS, AND FORMAL CHARGES
(Arthur Cammers, 2019)
Why are molecular formulas inadequate to define molecules?
Let’s examine the molecular formula C2H6O. Ethanol and
dimethyl ether bear very different chemical properties despite having the same
molecular formula. Molecules that have the same molecular formula but differ in
atomic connectivity, are termed constitutional isomers. The way that
atoms are arranged play a major role in how they react in solution with other
molecules. Therefore, discussing electronic properties of molecules is the
first thing we need to accomplish.

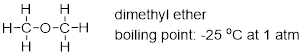
Much of what follows will be review for you because the
prerequisite of Organic Chemistry is General Chemistry, which always introduces
■ Lewis dot structures. Lewis structures
represent molecules by demonstrating their atom connectivity allowing us to
communicate symbolically. There are a few concepts that you need to bear in
mind to apply Lewis Structures effectively in organic chemistry:
1. Electrons
connect nuclei by virtue of their attraction to two or more nuclei.
a. Yes,
one-electron can bond two nuclei, but two electrons bond them much better.
b. When
only two electrons bond two nuclei we call this a σ bond (pronounced “sigma”
like the corresponding Greek letter).
c. Only
two electrons ‘fit’ in a bond, but double and triple bonds can form between
nuclei. In the following chapters we will unpack this concept further.
d. When
more than two electrons bind to two nuclei, these extra electrons must occupy
π bonds (pronounced “pi” like the corresponding Greek
letter).
2. ■ Valence
bond theory states that only valence electrons make bonds.
a. There
are other electrons, often referred to as core electrons or inner shell
electrons, that we can think of as very low-energy lone pairs that do not
participate in chemical change.
3. Better
Lewis structures have 8 electrons around any second-row elements (Li to Ne) and
2 electrons around the first-row elements (H and He) whenever possible.
Remember your many discussions of the ■ octet rule when
you studied General Chemistry.
Tackling a few example problems is the best approach from here
to review the construction of Lewis structures. In these examples while you are
reading try to remember your General Chemistry and do the problem first before
you look at the stepwise solution to the problem.
Example 1.2.1 Draw a bond-line structure
of ammonia, NH3.
Solution: First,
we will count electrons. Then we will find a reasonable way to connect the
atoms and place remaining electrons in our structure without violating any
rules.
Step 1.
Count the valence electrons.
 When we consult the ■ periodic table, we note that nitrogen is element
number 7 and it is the fifth element in the second row. To balance the charge
of the 7 protons in the N atom we need 7 electrons, but 2 of those are first
row electrons. The five electrons in the second row concern us the most as
these are the valence electrons – the electrons that reside in the outermost
shell surrounding the atomic nucleus. The number of valence electrons for each
neutral atom is equal to the atom’s main group number found in the periodic
table. These electrons determine the chemistry of the atom. The hydrogen atoms
have one valence electron each and there are three of them. Counting the
valence electrons in NH3 gives us:
When we consult the ■ periodic table, we note that nitrogen is element
number 7 and it is the fifth element in the second row. To balance the charge
of the 7 protons in the N atom we need 7 electrons, but 2 of those are first
row electrons. The five electrons in the second row concern us the most as
these are the valence electrons – the electrons that reside in the outermost
shell surrounding the atomic nucleus. The number of valence electrons for each
neutral atom is equal to the atom’s main group number found in the periodic
table. These electrons determine the chemistry of the atom. The hydrogen atoms
have one valence electron each and there are three of them. Counting the
valence electrons in NH3 gives us:
N: 1 atom x
5 e− = 5 e−
H: 3 atoms
x 1 e− = 3 e−
Total = 8
valence electrons
Step 2.
Place the atoms together so they share pairs of electrons to make complete
octets.
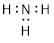
After we
use 6 electrons to share between N and the three H atoms, we are left with two
electrons (8 −6 = 2) which can sit on the N atom.
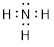
Now
counting all the electrons, we see that we have used 8 valence electrons in the
structure.
Step 3. In
organic chemistry we will show the bonded electrons as lines and use dots for
the non-bonded electrons.
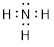 is simplified to
become
is simplified to
become 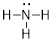 or
or 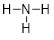
It is okay
to draw either structure when referring to ammonia. In the case on the right,
the lone pairs are understood to be there.
Sometimes people draw structures with implicit lone pairs; in
other words, sometimes people do not draw them on the structure. The rule of thumb is that lone pairs do not
have to be drawn on bond-line structures, but formal charges should always be shown. Charges always are explicit; if the
electrons were really missing, we would have to indicate the molecule has +2
formal charge (we will discuss how to calculate formal charge in Section 1.2.1);
thus, the lone pair is implied on the last structure above.
Instead of Lewis structures, we call these bond-line
structures. Bond-line structures, which are also called line structures
and skeletal structures, are quicker to draw, but we always
understand them as Lewis structures, meaning we know that each single bond is
made of two electrons.
1.2.1 Formal Charge
The formal charge (+ or –) is a number that we ascribe to atoms
in line structures. Formal charge is simply the number of protons in the
nucleus minus the number of electrons around the nucleus. It is a way of
keeping track of electrons and doesn’t necessarily represent the location of
charge in a molecule, but nonetheless, it is necessary to know how to assign
formal charges to become proficient in organic chemistry.
The calculation of formal charge is below:
FC = valence charge – (non-bonded valence electrons) – ½
(bonded valence electrons)
The valence charge is a positive number: It is simply the
charge of the nucleus without the valence electrons. To determine this number,
start with the left side of the ■ periodic table and count from left to right
until you get to the atom of interest. For example, the B atom has 3 valence
electrons, C has 4 valence electrons, etc.
Example
1.2.2 Draw the
Lewis structure of the cation +NH3, which could also be
written as NH3+ or [NH3]+. Put formal
charges on the appropriate atoms.
Note: There
is one fewer electron
than there are protons in the molecule.
Solution: When determining the Lewis
structure for an ion, we must adjust the number of electrons to account for the
net electric charge of the ion. A negative charge on an ion represents an
excess of electrons; however, a positive charge on an ion represents a loss of
electrons.
Step 1. Count the valence electrons:
N: 1 atoms
x 5 e−= 5 e−
H: 3 atoms
x 1 e− = 3 e−
- 1 for the
positive charge
Total = 7
valence electrons
Step 2. Put the molecule together as
indicated by the formula.
Using the
logic above, we now have this 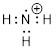 , which should be written as
, which should be written as 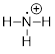 .
.
Step 3. Check your formal charge
assignments before concluding work on a problem.
For the H
atoms, FC = 1 – 0 – ½ (2) = 0
For the N
atom, FC = 5 – 1 – ½ (6) = +1
Note: In all
structures, the sum of the formal charges must equal the molecular charge.
Note: When including
a formal charge, you should circle it. This will help make sure that your
positive charge is not mistaken for a plus sign and that your negative charge
is not mistaken as a stray pencil mark.
Note: When including +1
or –1 formal charge, do not write the number 1. Only the + or – symbol surrounded by a circle
is needed: 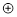 or
or  .
.
Exercise 1.2.1 How did we know to draw the molecule with a positive
formal charge on N (left) rather than a half charge each on N and one of the H
atoms (right)?
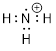
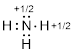
Example
1.2.3 Draw the
Lewis structure of (CH3)2CNH2+.
Note: In
this case, the way we should connect the atoms is indicated by the formula.
This is not always the case. The formula could have been presented as C3H8N+,
and in that case we would have more liberty in how we could correctly connect
the atoms with electrons.
Solution:
Step 1. Count the valence electrons: C =
4, H = 1, N = 5, −1 for the positive charge.
C: 3 x 4 =
12
H: 8 x 1 =
8
N: 1 x 5 =
5
- 1 for the
positive charge
Total = 24 valence electrons
Step 2. Put the molecule together as
indicated by the formula.
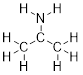
Step 3. Count the electrons used so far
and compare that to the number available: There are 11 bonded pairs of
electrons = 22 electrons. There are 24 electrons that we must use (they must go
somewhere).
Step 4. Notice in the structure above C
and N do not have 8 electrons. They both have 6 electrons around them. We can
fix this by connecting C and N with the remaining two electrons.
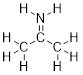
Still something
is missing. Even our new method to abbreviate Lewis structures never omits
formal charges. When we calculate the formal charges for the C atoms, we get
zeros because the valence of C = 4 and there are 8 bonded electrons to the C
atoms in every case:
FC = 4 – ½
(8) = 0
When we
calculate the formal charge for the N atom:
FC = 5 – ½
(8) = +1
We finish
the structure by adding the FC to the N atom.
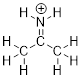
Since
organic structures have so many C atoms with H atoms connected, we further
abbreviate these atoms in bond-line structures implicitly. In the structure
above, we drew it with C and H explicit. The same molecule with C and H atoms
implicit is shown below. It is okay to draw the N-H bonds or represent the
group as “NH2”.

Note: All
heteroatoms (anything besides C and H) and any hydrogen that is attached to a
heteroatom must always be shown when drawing bond-line structures.
Alternate
Solution for Example
1.2.3
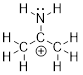
Step 2. Put
the molecule together as indicated by the formula and put the electrons on the
most ■ electronegative atoms.
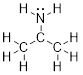
Step 3.
Calculate the formal charges.
Example
1.2.4 Draw the
Lewis structure of the methoxide anion, CH3O–.
Solution:
Step 1. Count the valence electrons for 1
C atom, 3 H atoms, 1 O atom, and add an electron to account for the negative
charge.
C: 1 x 4 =
4
H: 3 x 1 =
3
N: 1 x 6 =
6
+ 1 for the
negative charge
Total = 14
valence electrons
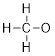
Step 2. Put the molecule together as
indicated by the formula. Since we know that carbon generally forms 4 bonds, we
can assume all 4 additional atoms will bond to carbon.
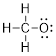
Step 3. Count the electrons used so far
and compare that to the number available: There are 4 bonded pairs of electrons
= 8 electrons. If we satisfy the octet rule for oxygen, then we will need to
add three lone pairs of electrons to the O. This makes 14 valence electrons,
which equals the amount calculated.
Step 4. We know from the formula that the
molecule has an overall negative formal charge. Upon calculating formal charge,
we find that it belongs on O.
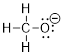
Note: In the examples above, when formal charges were
included, the charge was either +1 or -1. While ions can have net charges of +2
and -2 and greater, you will never see a formal charge on an atom other
than 0, +1, or -1 in a reasonable representation of an organic molecule or ion.
Example
1.2.5 Draw a
bond-line structure for CH3CH2CH2CH2CHCH2.
Solution:
Step 1. Count the valence electrons for 6
C atoms and 12 H atoms
C: 6 x 4 =
24
H: 12 x 1 =
12
Total = 36
valence electrons
Step 2. Put the molecule together as
indicated by the formula.
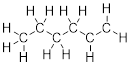
Notice that
all the C atoms are connected to C or H by 4 bonds except the two C atoms on
the right side.
Step 3. The two C atoms on the right side
do not have a full octet of electrons. They each have 6 total valence
electrons. If we examine the total number of valence electrons in our molecule
from Step 2 you will recognize that we have utilized 34 valence electrons and
still have 2 additional valence electrons to add. We should use this pair of
electrons to make another bond between the two C atoms filling each of the C
atom’s valence shell with 8 electrons.
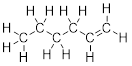
Step 4. Draw the structure again,
removing implicit C and H atoms, using bond-line structure.

Note: We don’t care how the structure is oriented. All
these structures indicate the same molecule.
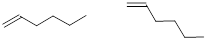

Exercise
1.2.3 Draw a
bond-line structure for (CH3)2CHCO2H.
1.3 DEGREES OF
UNSATURATION (DU)
(Arthur Cammers, 2019)
A molecule is termed saturated
when it possesses its maximum number of hydrogen atoms. A compound with fewer
than its maximum number of H atoms is termed unsaturated. Decreasing the number of hydrogen atoms by two adds a degree
of unsaturation (DU). In some textbooks, you may see this term called the hydrogen
deficiency index.
Each DU indicates a ring or a π bond. For a saturated
compound, in which there are no degrees of unsaturation, there will be no rings
and no π bond. Compounds with one DU have either one π bond or one
ring. A compound with 2 DUs will have two π bonds, one π bond and one
ring, or two rings. In the examples below in which all compounds have four
carbon atoms, the molecular formula is the same when the number of degrees of
unsaturation is the same.


Calculating the degrees of unsaturation is a very useful
shortcut that chemists use when the task involves going from formula to
structure.
For any neutral molecule,
DU = 1 + #E4 – ½ #E1 + ½ #E3
where #E4 = number of elements that bond 4 times, and #E3 =
number of elements that bond 3 times, and #E1 = number of elements that bond
one time with neutral formal charge.
Upon calculating the DU for a molecular formula, we can
determine several structural features of the molecule. The chart depicts
possible combinations of structural features depending on what DU you
calculate. If a DU of zero is obtained this means the molecule must be fully
saturated and therefore have no rings, double or triple bonds.
|
DU
|
Structural Components
|
Examples Containing 6 Carbon Atoms
|
|
π bonds
|
rings
|
|
0
|
0
|
0
|
|
|
1
|
1
|
0
|
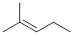
|
|
0
|
1
|

|
|
2
|
2
|
0
|
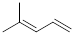
|
|
0
|
2
|

|
|
1
|
1
|

|
|
3
|
3
|
0
|

|
|
0
|
3
|
 * *
|
|
2
|
1
|

|
|
1
|
2
|

|
|
4
|
4
|
0
|

|
|
0
|
4
|
N/A for C6H6
|
|
3
|
1
|

|
|
etc., as long as
the sum of π bonds + rings = 4
|
Note: The molecule cannot possess a charge and must
have an even number of electrons to simply apply DU to the molecular formula to
unveil possible structural features!
Example
1.3.1 Draw a
bond-line structure for the formula C6H10.
Solution:
Step 1. Determine the degrees of
unsaturation based on the molecular formula.
DU = 1 + 6 −
½ (10) = 2
Two degrees
of unsaturation means that there is some combination of two bonds in excess of
a single bond between any two atoms or a ring. In other words, structures
matching this formula will have two π bonds, two rings, or a π bond
and a ring.
Step 2. Draw structures with the correct
number of C atoms and the correct DU features. You don’t have to count
electrons, or hydrogen atoms. Molecular formulas do not indicate how the atoms
are connected. If you need to draw a structure for C6H10
you are free to present any structure of the family of molecules with this
molecular formula. Some examples are shown below.


Twins or triplets are people with the same parents, likewise we
call these molecules isomers because they were built with the same number and
kinds of atoms. We are going to revisit the concept of isomers in much greater detail
soon.
Exercise 1.3.1.
Can you think of
a few more isomers with molecular formula C6H10? Keep the definition of DU in mind when
answering this question.
1.3.1 Using DU for Molecules with Other Atoms
We have more to discuss about using DU to go from molecular
formulas to molecular structures. How do
you know which elements are E4 or E1 and so on? Let us reflect on our General
Chemistry background while we look at the ■ periodic table. Remember that simple
application of DU to the molecular formula is only feasible if the molecule is
neutral and has an even number of electrons.
#E4 Elements: Due to
the manner electrons occupy space around elements, the C atom tends to bond 4
times. It has a valence of 4 and atomically the chemistry of the carbon atom is
thought of as
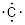
which can combine with
elements that bond once like H• to make methane, CH4.
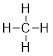
This structure obeys the octet rule with 8 electrons around the
C atom. The elements below the second row in the periodic table have similar
chemistry, so Si is also a #E4 element.
#E3 Elements: To the
right of C we find N which has 5 valence electrons. In its obedience of the
octet rule, the chemistry of the nitrogen atom is thought of as having one lone
pair, making three electrons available to form bonds.
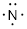
Nitrogen combine with elements that bond once like H• to make ammonium,
NH3.
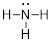
Thus, N is an E3 element in the DU formula for neutral
molecules.
B in neutral structures, like BH3, also bonds 3
times. In these structures, the B atom violates the octet rule, which is fine
for neutral structures that include boron.
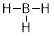
We will see in our studies that the octet rule still operates
with molecules that include B because boron atoms tend to bond with electrons
to make charged structures, but remember when this happens, these structures are
beyond the scope of DU because they are charged. The elements below the second
row in the periodic table have similar chemistry, so P is also a #E3 element.
#E2 Elements: Beryllium (Be) and oxygen (O) are E2
elements in neutral molecules; they bond 2x. Oxygen has 6 valence electrons, in
obedience to the octet rule the chemistry of oxygen.
Oxygen tends to bond 2x and obey the octet rule by also having
two lone pairs.
In neutral structures the chemistry of Be is mandated by its
two valence electrons, so it is a #E2 element. It violates the octet rule (see
example BeCl2). However, similar to boron, in molecules the Be atom
tends to want to fill its octet by bonding with electrons in other atoms.

Think about why #E2 does not appear in the DU formula. Think
about why we count half the H atoms and all the C atoms in the formula. Let us
start with molecular hydrogen, H2, which must be DU = 0 because
logically it can have no rings or double bonds without violating the bonding
rules for the H atom, and DU = 1 – ½ (2) = 0. The atoms in H2 are the
reason we have the 1 in the formula.
Between the two H atoms we can put CH2 to get CH4
and the structure still has DU = 0. This is why we add one DU unit for every C
atom and subtract half a DU unit for each H atom in the DU formula. This is
also why we can ignore the elements that bond 2x because we can use the O atom
and other atoms that bond 2x in the same manner that we used CH2
without changing DU. For example:
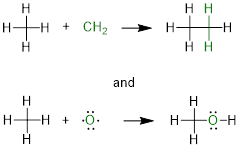
Both the ethane and methanol molecules have no degrees of
unsaturation. Therefore, atoms or structural fragments that bond 2x must
contribute zero to the DU of the formula. In the case of CH2, we add
1 and subtract ½ (2) to get zero; in the case of the O atom, we ignore it.
#E1 Elements: Of
course, the H atom is an E1 element and so is the F atom because octet
occupation leads us to chemistry wherein only one bond can form.
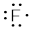
Single vs. Double vs. Triple
Bonds: For now we are using multiple
bonds simply to satisfy the octet rule, but you may already know that there is
a difference between multiple lines we draw between atoms in molecular
structures when there is more than one bond between two atoms, i.e. when we
introduce unsaturation in the structure. In the case where there are two bonds
between two atoms, one of these is a single bond, a sigma (σ) bond and the
other is a pi (π) bond. In the case where there are three bonds between
two atoms one of these is a σ bond and the other two are π bonds. We
will soon have to discuss the intrinsic differences in structure and reactivity
of these two bonds in detail, but we will need more theory to do so.
Summary: We know
from our general chemistry background that the elements in the columns of the
periodic table have similar chemistries.
Thus H, Li, F, Cl, Br are all #E1 elements in the DU formula. Likewise, O,
S, and Be are #E2 elements, and B, Al, N, P, and As are #E3 elements. Finally, C,
Si, and Pb are #E4 elements.
Example
1.3.2 Draw a
bond-line structure for the formula C20H35NOSi2BrCl.
Solution: The scale of this problem
is big, but with the background above, scale becomes more trivial. This
ridiculously large scale of atomic content and possible structural features for
this example was chosen to show that scale becomes manageable with good
formulism.
Step 1.
Find out something about the structure by
calculating DU = 1+22−½ (37) + ½ = 5;
22 because
there are 20 C and 2 Si atoms; C and Si form 4 bonds in neutral molecules
37 because
there are 35 H atoms and 2 halogen atoms; these bond once
+½ is for
the N atom
DU = 5
means that there are 5 bonds in excess of a single bond between any atom or
some combination of rings and multiple bonds to equal DU = 5.
Step 2. We can just draw neutral
bond-line structures (Lewis structures) that answer the formula without
thinking about counting electrons or H atoms.
While
drawing, make sure there is one Cl, one Br, two Si, one O and one N atom in the
molecule. Make the Si and C atoms bond 4x and the O atom bond 2x and the N atom
bond 3x. We make sure that there is enough unsaturation to equal DU = 5 by
including structural features like double bonds, triple bonds, and /or rings.
In the
first structure below there are 4 rings and a double bond which gives DU = 5.
In the next structure there is a triple bond and 3 double bonds which also sum
to DU = 5.
Two
Solutions (there are many, many more):
When you look at the structures remember that the H atoms on
the C atoms are implied. The C atoms are also implied when the lines change
direction or terminate; at the end of every single ‘line’ there are 3 H atoms
on a C atom unless it bears a formal charge. At each vertex there are two H
atoms if there are only single bonds at the C atom and there is one H atom if
there is a double bond at the C atom, and so on.
Note: These
structures may seem random … these structures are random. There are zillions of
isomers for this formula. Organic Chemistry is amazing! Due to the diversity in
bonding and atomic content, a chemist with a little training can make the
world’s supply of something in a few days in the lab!
Exercise 1.3.2
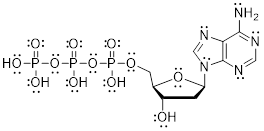
dATP is an important molecule in the
synthesis of DNA and energy production. Add the missing lone pairs to dATP.
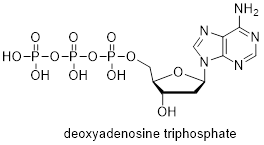
Exercise 1.3.3
Consider
possibilities for the bond-line structure for the diol propylene glycol, C3H8O2.
This is a common ingredient in ■ antifreeze; you can click the link and check
the line structure. Did you happen to guess right? Did you draw an isomer?
Note: Even looking up
encyclopedic information on antifreeze contains a bond-line structure for a
common ingredient; this fact should pique your curiosity about the importance
of and the broad information in organic chemical bond-line structures. After
you take this course, you will look for these structures and tap your chemical
education to learn more about the substances that you research!
1.4 RESONANCE AND ELECTRON PUSHING
(Ashley Jolly Steelman and Susan Odom, 2019)
As chemists started to develop a deeper understanding of the
bonding in molecules, it was found that there are inadequacies in numerous
bond-line structures. In order to resolve these inaccuracies, chemists draw
resonance structures. A resonance
structure is drawn when one bond-line or Lewis structure cannot fully
describe the bonding that takes place between neighboring atoms. Examine the
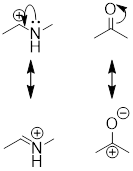
two structures of the allyl cation. The positive formal charge is delocalized
onto C1 and C3, meaning the charge is
spread over two locations. The formal charge cannot be isolated at the two
different locations, because in the real structure electrons move freely.
Experiments have shown that the structures below must represent the same
molecule. Shown below are the two resonance structures of the allyl cation, [CH2CHCH2]+.
Both resonance structures, which are shown to either side of the double headed resonance
arrow ( ), contribute equally to the electronic structure of the
allyl cation.
), contribute equally to the electronic structure of the
allyl cation.
It is important that you know that resonance structures depict
the location of electron density within one molecule. The actual structure of
the allyl cation is a combination of all resonance structures melded together.
This is represented by a resonance hybrid – a combination of each
individual resonance structure.
Note: The double headed resonance arrow is not the same
as an equilibrium arrow. Resonance structures are not in equilibrium with each
other.
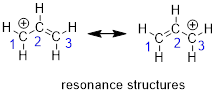

Note: any time that two resonance structures are mirror
images of each other, they will contribute equally to a species’ electronic
structure.
Two structures are resonance structures if they only
differ in the placement of π bonds and electron lone pairs; the position
of σ bonds do not change. In the next few sections, we will learn more
about resonance structures, including converting between multiple structures as
well as determining what structures are reasonable and are the most important
contributors.
You might wonder why it is important to consider multiple
representations of the same molecule or ion when each valid resonance structure
is a Lewis structure that represents the species of interest. The structures
are only different because we rearranged bonds and charges. The reason we need
to consider resonance structures is that considering the position of charges
and electrons will allow us to begin analyzing the reactivity of a molecule
specifically looking at where a molecule’s electron density is located. In
order to draw and recognize resonance structures of a given species, we need to
talk about a couple rules:
1) We tend to move electrons located in π bonds or in
electron lone pairs because disrupting σ bonds drastically increases
the energy. These electrons must be isolated in a p orbital, which we will talk
about in a deeper sense later. However, recall from general chemistry what
single, double, and triple bonds consist of:
·
single bond: one σ bond
·
double bond: one σ bond and one π bond
·
triple bond: one σ bond and two π
bonds
This means that we will avoid breaking a single bond in a
resonance structure. We will avoid breaking a π bond without having the
structure recover electron occupation at an electronegative atom. We should focus
on moving electrons in double bonds, triple bonds, or electron lone pairs.
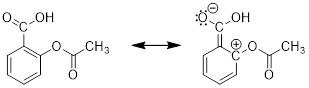
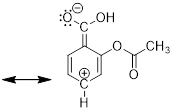
2) The overall charge of a system must remain the same. Examine
the three resonance structures of Aspirin and note that the net charge is the
same in each structure. The first structure is neutral and therefore, we will
see that the second and third structure carries a positive and a negative
formal charge, which cancel one another out so that the structure remains
overall neutral.
3) The bonding framework must remain intact. We will use
curved arrows to depict the movement of electrons throughout this entire
course. A common mistake of beginning organic chemists is to use curved arrows
to indicate the movement of atoms or positive charges but this will NEVER
occur. A curved arrow is only
used to depict the movement of valence electrons in resonance structures or
reaction mechanisms. Every curved arrow has a tail and a head. Each arrow
indicates where a pair of
electrons originates (tail of the arrow) and where they are moving to (head of
the arrow).

Let us tackle the following example to demonstrate how curved
arrows are used to push valence electrons.
Example
1.4.1 Draw the
resonance structure that is indicated by the curved arrows shown. Be sure to
include formal charges.
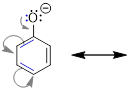
Solution: First, we will draw what
did not change from our original structure, then – for the electrons that moved
(highlighted here in blue) – we will determine their location in the second
resonance structure, then assign formal charges.
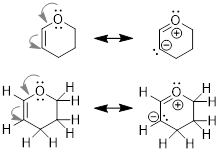
Step 1. The tail of each arrow depicts
where each set of electrons is moving. The lone pair of electrons on oxygen
will move to form a double bond between oxygen and carbon. The double bond at
the top left of the ring is being moved to a carbon-carbon double bond to the
left of the ring. The double bond at the bottom left of the ring is being moved
to a lone pair of electrons on the bottom carbon of the ring.
Note:
The tail and head of each arrow needs to be placed in very precise locations.
Specifically, if you are moving a pair of electrons to form a double bond then
you need to place the head of your arrow in the middle of the bond. However, if
you are moving a pair of electrons to a lone pair on a specific atom then the
head of the arrow needs to be drawn directly to the atom.
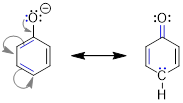
Step 2. We now must assign formal
charges. Recall that the overall charge of the molecule must remain the same.
Our structure started with an overall negative formal charge and we will find
that the newly drawn resonance structure will also have an overall negative
formal charge that has been moved to carbon.
Give the exercise below a try. Make sure you can do this
problem correctly before proceeding!
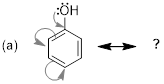
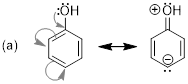
Exercise 1.4.1 For each of the structures below,
draw the resonance structure that is indicated by the curved arrows shown,
showing all electron lone pairs. Be sure to include formal charges.
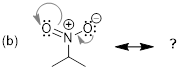
1.4.1 Moving Electrons without Violating Rules
When you first start drawing resonance structures, it is easy
to get confused about which way to move π bonds and electron lone pairs.
Especially when you’re working with bond-line structures in which H atoms are
implied, you can move bonds and violate the octet rule without realizing it.
Therefore, it is a really good idea to add implicit H atoms and implicit
electron lone pairs to your drawings until you are sure that you’re comfortable
drawing resonance structures without making errors.
Let us look at an example of a right and wrong way to move
electrons to create a second resonance structures from the same starting point.
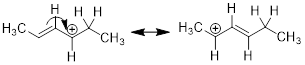
In this conjugated system, we can only use three of the carbon atoms to house
delocalized electrons.
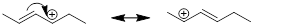
This is the only arrow you can draw that leads to a good
resonance structure

error: moving pi bond toward an atom that already contains
four sigma bonds

error: moving a sigma bond - you can only move pi bonds and
electron lone pairs
With the implicit H atoms incorporated into the structure, we
can be more specific about why the second and third options are incorrect.
Still good!
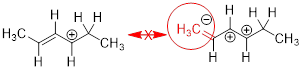
octet rule violation -
this structure is completly invalid
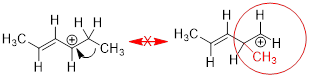
different sigma bond connectivity - this is an isomer
This brings us to recognizing some common patterns in moving
delocalized electrons to draw resonance structures. A summary of common arrow
pushing patterns in drawing resonance structures is shown below. If you follow
these patterns, your resultant structure should be reasonable and without octet
violations. If ever in doubt, though, add implicit H atoms to your structures,
which will make it easier for you to catch errors.
Acceptable Curved Arrow Use to Yield Reasonable Resonance
Structures

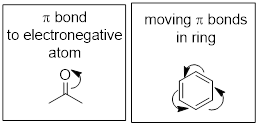
Let us practice some arrow pushing by drawing the resonance
structures and resonance hybrids that represent each pair of resonance
structures.
Exercise 1.4.2
(a) Redraw the following bond-line
structures to show all implicit H atoms and implicit electron lone pairs;
retain the curved arrows. (b) Then draw the resonance structures that result
from the curved arrows, again showing implicit H atoms and implicit electron
lone pairs. (c) For each example, draw a resonance hybrid that represents a
combination of each of your pairs of resonance structures.
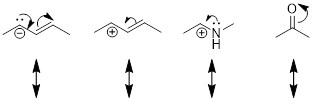
Note: Always
check to make sure your charges are balanced (same net charge in each resonance
structure) and that you have not violated the octet rule for second row atoms.
Exercise 1.4.3
For dihydropyran,
shown below, examine the curved arrows showing movement of an electron lone
pair and/or the π bond. Only one example, a-e, shows the arrow(s) that
would lead to a valid resonance structure. Without adding implicit H atoms, can
you tell which one choice leads to a resonance structure?
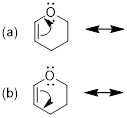
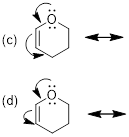
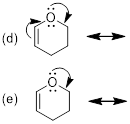
Now, draw
the structures again and include the implicit H atoms. Is it easier to see how
all but one set of arrows violates the octet rule?
1.4.2 Estimating the Importance of Resonance Structures
Not all resonance structures contribute equally to the overall
resonance hybrid. This is the reason we avoid showing resonance structures that
involve the movement of electrons in σ bonds without some energetic recovery
from putting electrons on electronegative atoms.

NOT A GOOD RESONANCE STRUCTURE! (Left structure) major
contributor - all atoms have filled octets and σ bonds are intact. (Right
structure) a minor contributor to the real structure that shows the polarity of
the C−O bond. The C atom lacks an octet; it only has six valence
electrons.
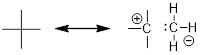
A WORSE RESONANCE STRUCTURE THAN THE ONE ABOVE! (Left
structure) major contributor - all atoms have filled octets and σ bonds
are intact. (Right structure) a RIDICULOUSLY minor contributor to the real
structure. Unlike the molecule with the O atom, the hydrocarbon resonance
structure (above lower right) recovers nothing from putting the extra electrons
on a relatively electronegative atom.
We need to be able to recognize the quality of each resonance
structure. The resonance with a better (lower energy) Lewis structure will be a
more significant contributor to the overall structure of the molecule. The
following rules will help you to evaluate which resonance structures are major
vs. minor contributors.
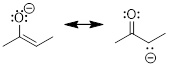
1) Look for the
resonance structure where every atom has filled valence shells (completed
octets). Examine the structures below.
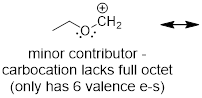
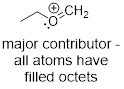
A GOOD RESONANCE STRUCTURE! Because the difference in
energy is not so big. The π bond is weaker than the σ bond, but the π
bond is better than no bond.
2) The structure with fewer formal charges. The
separation of charge costs energy. This is ■ Coulomb’s Law
which states that the potential energy increases as a function of the square of
the distance between two charged bodies.
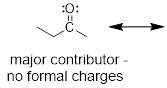
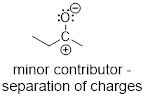
3) If a resonance structure bears a negative formal
charge, the structure that places the negative charge on the most ■ electronegative
atom will be more significant (lower in energy). Do you remember that term from
General Chemistry? If not refresh your concept by clicking the link. It is the
rough measure of atoms to attract electrons. The lower the energy of the
electrons around an atom the more electronegative the atom is.
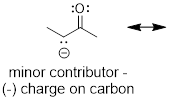
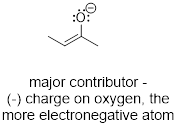
Example
1.4.2 Draw all significant resonance
structures for the molecule below and determine which structure would be
considered the most significant.
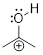
Solution:
Step 1. Locate the π electrons
that can move in resonance. A positive formal charge represents an atom that
has lost electron density and means that, in most cases, that atom can accept
electron density. A pattern that you will notice is that π electrons can
be moved towards carbocations because they can accept electron density. You
might also notice that oxygen has two lone pairs of electrons. One of these
lone pairs can be moved towards the positive charge.
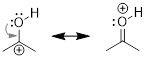
Step 2. In this example, one
resonance structure is more significant than the other. The structure on the
left exhibits a carbon atom that lacks a full octet (six total valence
electrons). The structure on the right exhibits atoms that all have filled
octets and a π bond. Therefore, the resonance structure on the right is
the major contributor.
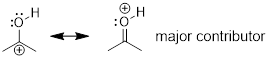
Now, use what you just learned in the example to try your hand
at the following exercise involving drawing and comparing resonance structures.
Exercise 1.4.4
(a) Draw a second resonance structure
for this anion, showing all electron lone pairs. (b) Determine which structure
contributes more to the resonance hybrid.
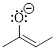
Exercise 1.4.5
(a) Draw the remaining resonance
structures for each species below. (b) In each case, determine which of the
resonance structures (of the originally provided structure and the answers you
provided) would be the most significant contributor to the ground state
electronic structure of each species.
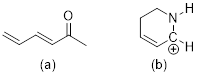
Exercise
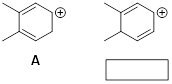
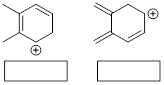
1.4.6 How are the
following structures related to cation A? Your choices are resonance
structures, isomers, and neither.
Exercise 1.4.7
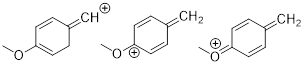
(a) Draw all good
resonance structures for the benzyl cation. (b) Does the methoxy group (OMe) help to stabilize the cation compared to having an H
atom in its place? Explain your answer.

1.5 X-RAY CRYSTALLOGRAPHY FINDING POSITIONS OF ATOMS
(Arthur Cammers, 2019)
Now we come full circle. Due to the strong interaction of light
with charged particles and with systems composed of such particles (molecules),
we can use electromagnetic radiation at X-ray wavelengths to look for atoms in
molecules. This phenomenon has a strong relationship to the discussion in the ■ first section
about the electromagnetic force and its pertinence to chemistry.
■ X-ray crystallography is utilized to find the
relative positions of atoms in molecules. The term indicates that the method
involves visualizing some hidden aspect of crystals with X-rays.
1.5.1 Why X-Rays?
One must use wavelengths at about atomic sizes for this to
work, typically ~0.1 Å range. Confirm this size range by looking at the ■ periodic table. Click on the carbon atom and look for
the parameter: ‘covalent radius’. This is the typical size of the atom in a
bond. This wavelength of X-ray has energy just below the energy required to
make ions out of neutral molecules (■ electromagnetic
spectrum just at the upper end of soft X-rays see the table in the
link). Light at this wavelength bounces off electron clouds around atoms
in molecules in crystals. Remember from your General Chemistry course that the
electron cloud determines atomic and molecular dimensions. If the X-ray
wavelength is longer, the reflections lack the resolution to ‘see’ the atoms. If
the wavelength is any shorter, molecules decompose.
1.5.2 The Spatially Periodic Crystalline State
For the technique to work, we also need crystals which have
repeat patterns of atoms or molecules in 3D. Many substances crystallize and we
have everyday experience of this phenomenon in the kitchen with sugar and salt.
■ NaCl forms a simple cubic
lattice (click the link; have a look at the perfectly periodic placement of Na
and Cl in the solid), but crystalline sucrose is more interesting. In the
crystal, sucrose molecules align in three dimensions due to attractive and repulsive
interactions when the electrons around the nuclei pack together.

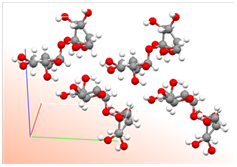
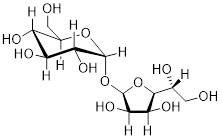
Figure A. Left: Sucrose crystals under a light
microscope. Middle: Four molecules arranged by Mother Nature in sucrose
crystals. White = H, Grey = C, Red = O atoms. Right: The bond-line structure of
sucrose. The experiment finds the C atoms; however, placement of the H atoms on
the molecule in this crystal structure are not experimental. The positions of H
atoms are more difficult to determine.
1.5.3 How It’s Done
The crystallographer mounts a small (~0.2 mm) crystal on a
glass fiber, nylon loop, or similar non-crystalline material and puts it in an
X-ray beam. Decreasing the temperature (for example to −40 °C) decreases
thermal motion in the crystal which affords better atomic resolution. The
instrument systematically rotates the crystalline sample in 3D while imaging
the diffraction pattern produced by the reflected X-rays. A computer algorithm
back-calculates from the positions of the spots in the data to determine the relative
positions of blobs of electron density, i.e. ‘atoms’ in the crystal.


Figure B. Left: goniometer on which a crystal is mounted
in preparation for data collection. Right: A 2D diffraction pattern obtained
for a crystal of sucrose at
−183 °C. Turning and tilting the crystal reveals different 2D
parts of the 3D diffraction pattern. The diffractometer digitizes thousands of
these images as a function of the tilt angle to the X-ray beam, and enough data
piles up to calculate relative positions of the C and O atoms in the molecule.
Data Credit: Sean Parkin, U. of Kentucky, ■ UK X-Ray
Crystallography Facility.
In this way, we unveil relative positions of atoms in
molecules. When we draw a double bond for example, we expect that the two atoms
connected by the double bond should be closer (atoms are held together more
tightly) than the average value we would get from a single bond between the
same two atoms. X-ray structures also show us the geometry of atoms—whether the
bonding pattern is planar (2D) or whether the atom in question has bonded atoms
in a 3D atom array.
Exercise 1.5.1
Test your
understanding. (a) Why are the H atoms more difficult to determine with X-ray
in crystallography? (b) What might you do to make them more apparent? Does this
pose further problems?
KEY TO CHAPTER 1 EXERCISES
(Susan Odom, 2019)
Exercise 1.1.1 Answer: See the ■ Periodic Table.
Exercise 1.2.1 Answer: We always want to show general
structures as lowest-energy structures. When we worry about chemical potential
energy, we are referring to the energy of electrons. The electrons
participating in bonding are low in energy so the missing electron will be
‘missing from the non-bonding (lone) pair of electrons instead one of the
bonded pair of electrons. You are going to have to make decisions like this in
the future when you draw organic chemical structures.
Exercise 1.2.2 Answer:
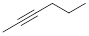
Exercise 1.2.3 Answer:
Exercise 1.3.1 Answer: There are many correct
answers to this problem. See if yours match any of these.
Exercise 1.3.2
Answer:
Exercise 1.3.3 Answer:

Exercise 1.4.1 Answer:
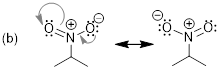
Exercise 1.4.2 Answer:
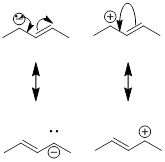
resonance structures that result from curved arrows
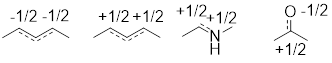
resonance hybrids based on the two resonance structures drawn above weighted
equally. There is not reason that they should be weighted equally, in general.
Exercise 1.4.3 Answer: Only the curved arrows
in example D does not result in structure that contains an octet rule
violation. See the answer with and without implicit H atoms.
Exercise 1.4.4 Answer:
Exercise 1.4.5 Answer:

Exercise 1.4.6 Answer:

Exercise 1.4.7 Answer:
(a)
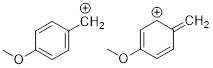
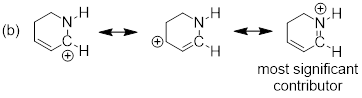
(b) Yes, because the electron lone pair is part of the π
system and can share the positive charge, this leads to greater stabilization
than if an atom without a lone pair were connected to the ring.
Exercise 1.5.1 Answer: (a)
H atoms are more difficult to determine than other atoms because they only have
one electron. (b) Work with shorter wavelength X-rays. A problem is
increasing the risk of materials decomposition.
CHAPTER 1 PRACTICE PROBLEMS
(Ashley Jolly Steelman and Susan Odom, 2019)
PP 1-1 Draw a bond-line
structure that has two rings for C10H18.
PP 1-2 Draw a bond-line
structure that has one ring for C10H18.
PP 1-3 Draw a bond-line
structure that has one ring for C9H8O4.
PP 1-4 The bond-line
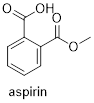
structure for C9H8O4 matches that of aspirin
(acetylsalicylic acid). Look at the structure of ■ aspirin. How many
CC double bonds are there? How many CO double bonds are there?
PP 1-5 Draw the bond-line
structure for each of the following compounds.
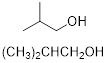
(a) (CH3)2CHCH2OH
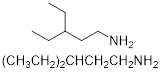
(b) (CH3CH2)2CHCH2CH2NH2
PP 1-6 Draw 4
constitutional isomers with the molecular formula C5H10O
using bond-line structures. Assume all non-hydrogen atoms have an octet of
electrons and no formal charge.
PP 1-7 A compound with
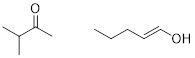
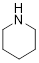
molecular formula C5H11N has no π bonds. Determine a
potential structure of the compound.
PP 1-8 The bond-line
structure for ■ cocaine
has 8 degrees of unsaturation. (a) Confirm this with the formula: C17H21NO4;
show the math. (b) Look at the structure in the link. In which structural
features of the molecule do we find the degrees of unsaturation?
Note: Any common molecular substance that we look up in
Wikipedia or elsewhere usually includes a bond-line structure. The structures
we are leaning about here are common information for any chemist to gain
insight about a substance, examples: (1) ■ capsaicin, (2) ■ GABA,
(3) ■ RNA, (4) ■ DDT, (5) ■ oxycodone, etc. This
list is functionally infinite because it grows annually.
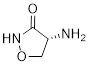
PP 1-9 Determine the molecular formula for the molecule cycloserine, an antibiotic used to treat tuberculosis.
PP 1-10 Add formal charges to the following molecules or
ions where necessary.
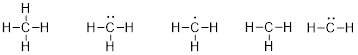
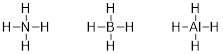
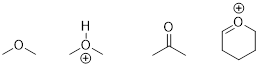
PP 1-11 To each molecule or ion below, add any implied
electron lone pairs. Then add formal charge where necessary to complete each
structure.
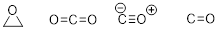
PP 1-12 The bicarbonate anion,
HOCO2–, has two equally good resonance
structures. Draw them and the resonance
hybrid that results when taking them into account.
PP 1-13 For each of the anions and cations, draw
the best resonance structure – the best being defined as the one that contains
the most bonds and fewest formal charges. In some cases, there are two
acceptable answers.
Anions:
(a) [SCN]– (b)
[H3CCO2]– (c) [CN]–
Cations:
(d) [H7C3]+ (e) [H3CO]+ (f) [HCO]+
PP 1-14 For each chemical formula, draw all
possible constitutional isomers. The number of possible isomers is indicated
after each chemical formula.
C3H7Cl (2
isomers) C4H10
(2 isomers)
C2H6O (2
isomers) C3H6Br2
(3 isomers)
C2H4O (3
isomers)
PP 1-15 Which compound is not a
constitutional isomer of 2-butene, CH3CH=CHCH3?
PP 1-16 For the following compound, determine
whether each electron lone pair localized or delocalized.
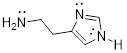
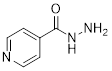
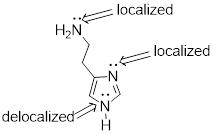
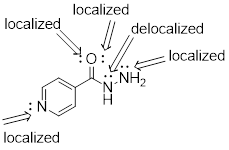
PP 1-17 Isoniazid is a drug used in the treatment of
tuberculosis and multiple sclerosis. Add all implicit electron lone pairs to
the drawing of the compound isoniazid – a drug used in the treatment of
tuberculosis. Then identify each lone pair as either localized or delocalized.
PP 1-18 Consider the following two compounds and
identify which has greater resonance stabilization. Provide a brief explanation
of your choice.
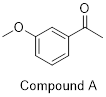
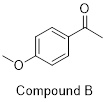
PP 1-19 Draw another resonance contributor to the
anion below in which all atoms have an octet. Show all electron lone pairs.
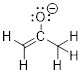
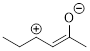
PP 1-20 Draw another resonance contributor of the
molecule below in which all atoms have an octet. Do not show implied electron
lone pairs and implied C and H atoms.
KEY TO CHAPTER 1 PRACTICE PROBLEMS
(Susan Odom, 2019)
PP 1-1 Answer: Here are a few examples of many
correct possibilities.
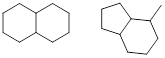
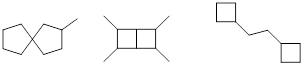
PP 1-2 Answer: Here are a few examples of many correct
possibilities.
PP 1-3 Answer: Here are a few examples of many correct
possibilities.
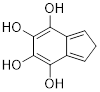
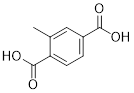
PP 1-4 Answer: Aspirin has 3
C=C bonds and two C=O bonds.
PP 1-5 Answer:
PP 1-6 Answer: Here are a few examples of many correct
possibilities.

PP 1-7 Answer: Here are a few examples of many correct
possibilities.
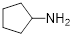

PP 1-8 Answer: (a) DU = 8. (b) Degree of
unsaturation include 3 for rings, 3 C=C bonds, and 2 C=O bonds.
PP 1-9 Answer: C3H6N2O2
PP 1-10 Answer:
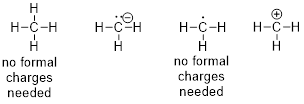
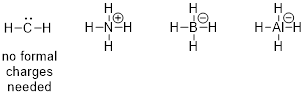
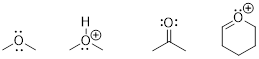
PP 1-11 Answer:
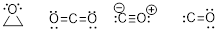
PP 1-12 Answer:

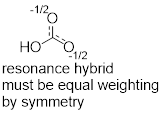
PP 1-13 Answer:
Anions: (a)
[SCN]- (b)
[H3CCO2]- (c) [CN]-
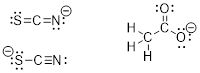

Cations: (d)
[H7C3]+ (e) [H3CO]+ (f) [HCO]+
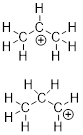
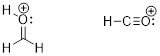
While this structure does not violate the rules, we will later
see that a hextet at a carbon atom with only one alkyl group - a primary carbon
– is very unstable. This molecule spontaneously rearranges.
PP 1-15 Answer:
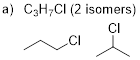
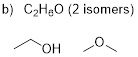
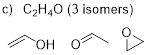

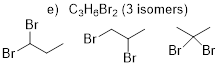
PP 1-15 Answer: D
is the only one with a different chemical formula. Without counting H atoms, by
acknowledging that it has 2 degrees of unsaturation, you know it has 2 fewer H
atoms than 2-butene and structures A, B, C, and E – all of which have 1 D.U.
and the formula C4H8.
PP 1-16 Answer: PP
1-17 Answer:
PP 1-18 Answer: Compound B has greater resonance
stabilization because one of the electron lone pairs in the methoxy (CH3O)
group is part of the π system. See the resonance arrows and resultant
second-best resonance structure below. If you try to use the same set of arrows
pushing for compound A – pushing the methoxy group’s lone pair toward the
carbonyl – you’ll end up violating the octet rule.
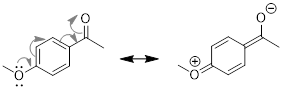
If you haven’t tried doing the same with compound A, try it!
It’s worth seeing why it won’t work!
PP 1-19 Answer: PP 1-20 Answer:

![]() ) indicates, and how it differs from the equilibrium arrow (
) indicates, and how it differs from the equilibrium arrow (![]() ).
). 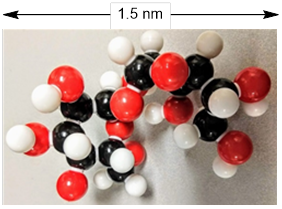 (Arthur
Cammers, 2019) (Image: Molecular model of sucrose. Credit: Arthur Cammers,
2019)
(Arthur
Cammers, 2019) (Image: Molecular model of sucrose. Credit: Arthur Cammers,
2019)  What is Organic Chemistry? Look at the
What is Organic Chemistry? Look at the 

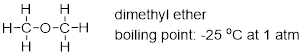
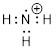 , which should be written as
, which should be written as 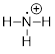 .
.