CHAPTER 2: MOLECULAR STRUCTURE - THE σ BOND

(Arthur Cammers, University of Kentucky, 2019)

Note: normally px, py and pz have subscripts, p_x, p_y and p_z the author dropped the subscripts for better readability.

Note: This and the next chapter are geared toward giving the reader a foundation for introductory structure and reactivity. Don’t focus on memorizing the facts. Focus on the arguments about the facts.

Learning Objectives:

1. Explain where atomic orbitals come from and what they are. (■■)

2. Why are orbitals necessary to model the behavior of electrons? (■■)

3. What is a node and what does the number of nodes in an orbital mean for the energy of the orbital? (■■)

4. Where does chemistry first occur in the cosmological story? (■■)

5. What is meant by conservation of orbitals? (■■)

6. Electron occupation of AOs and MOs define the size of atoms and molecules. (■■)

7. How can methane make equivalent bonds out of one s and three p atomic orbitals? (■■)

8. What is the definition of sp³ hybridization? What is being mixed? (■■) (■■ CH₄)

9. What is the definition of sp² hybridization? How many pure p orbitals are on the atom? (■■)

10. What is the definition of bonding, antibonding, and non-bonding in terms of orbitals? We’ve used the term non-bonding before; was the definition in the preceding chapter the same as in this chapter? (■■ start with H₂ as a model for σ bonds)

11. Why is CH₃^– tetrahedral? Why is CH₃⁺ planar? (■■)

12. Explain the HCH bond angle in CH₄. (■■)

13. Explain the HCH bond angle in CH₃⁺. (■■)

14. Define improper dihedral angle. (■■)

15. Explain the molecular motion in CH₄, CH₃⁺, •CH₃, and CH₃^– in terms of hybrid MOs. (■■)

2.1 ATOMIC ORBITALS (AOs)

Image: Zome^TM Models, a Tetrahedron Inscribed in a Cube Centered in Cartesian Coordinates. Arthur Cammers, 2019.

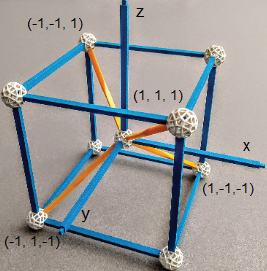In previous sections, we drew structures based on the number of valence electrons for the construction of valence bonds and the octet rule. We assigned atomistic formal charges in the structures such that when summed, the charge of the molecule results. It is very easy to take these 2D cartoons as good models for molecular behavior, but they are not. Line structures ignore many aspects of electronic behavior that is important to explain molecular structure and reactivity. In this section, we wrestle with descriptions of the space that electrons occupy.

Electrons have wave-like properties. This means there are parameters necessary to describe the electron that allows two or more electrons to interact constructively or annihilate each other. Therefore, when you compare the behavior of two separate electrons with the behavior of two electrons in proximity, we get complex systems much beyond simple repulsion of two particles of the same charge. Due to this weird property of electrons, we must use math that models the interactions of waves.

The ■ time-independent Schrodinger equation is a differential equation for which mathematical solutions are also equations that describe where in the volume around the nucleus that we are most likely to find electrons; these equations are referred to as wave functions; when these equations pertain to atoms they are called atomic orbitals (AOs). Surfaces (spheres, planes, curved surfaces) cut through these AOs at which electron density drops to zero; these surfaces are called nodes. Across the node the sign of the AO always changes indicated with red (negative) and blue (positive) in Figure A. Do not confuse the mathematical sign of the orbital with + or − charge; the two are unrelated. Charge is a unique property of a particle that assigns its strength of interaction with the electromagnetic field. The sign of the AO is a parameter of the AO that allows it to interact in a wave-like manner (constructively or destructively) with another AO.

Figure A. X, Y, Z graphs of solutions to the Schrodinger equation, wavefunctions (AOs) s orbitals for principle quantum number N = 1, 2 and 3.

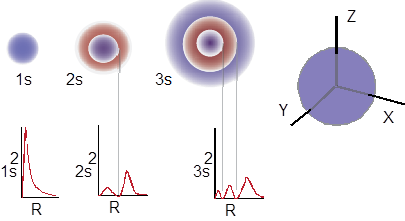
At the far right of Figure A is a spherical distribution of electron density – an s atomic orbital. Cutting through the center with any plane shows the internal radial nodes of the AOs 1s, 2s and 3s, as a function of the principle quantum number. The square of the AO indicates electron population (graphs below the AOs); these values are positive, with nodes where the probability of finding the electron = 0.

Notice something else very interesting about the diagrams in Figure A. There is at least a point node for each of the orbitals and indeed for all AOs. When you were studying General Chemistry did you ever ask yourself why the electron does not just stick to the nucleus and stay, perhaps when samples approach 0 K at which point thermal motion ceases? If the electron is attracted to the nuclear charge why doesn’t it just sit there like the opposite poles of two magnets stick to each other? The fundamental reason that there is always a point node at the nucleus is due to the Heisenberg Uncertainty Principle. Although it may sound like Heisenberg is saying something about our ability to know, he is more making a statement about the physical nature of atomic particles in general. The natural fuzziness of stuff puts a node at the atoms of all AOs; the electron cannot stay at the nucleus. If not for quantum mechanics, if would all collapse into a black hole.

“…translated into English from a variety of original German terms. Heisenberg originally called the concept Ungenauigkeit (inexactness) or Unbestimmtheit (undeterminedness), whereas his mentor and collaborator Niels Bohr often used Unsicherheit (unsureness). Today in German the most commonly used term for the principle is Unschärfe (blurredness or fuzziness).” Wikipedia

■ Heisenberg Uncertainty Principle

For principle quantum number N=2, there are four unique equations that solve the Schrodinger equation; one is described graphically in Figure A – an 2s orbital with one radial node. The other 3 equations describe electron density distributions with planar nodes at the three Cartesian planes YZ, XZ, and XY. Unlike the 2s AO, these AOs with planar nodes are directional. The AO with nodal YZ plane is the 2px AO (lies along the x-axis), nodal XZ plane defines the 2py AO, and nodal XY plane defines the 2pz AO. The 2px orbital, another solution to the Schrodinger equation is described graphically in Figure B. The other two directional 2p AOs are the same except that they are directed along the other two Cartesian axes.

Remember that AOs are just possible equation solutions to Schrodinger’s differential equation to model wave behavior. As N increases so does the average distance of the electron to the nucleus and thus the energy of the multibody system increases. In general, when we go from s to p AOs of the same quantum number the average distance also slightly increases with a concomitant increase in energy. If we keep playing this mathematical game progressing from s to p orbitals and on to d orbitals and we look at the general trends of the elements as a function of atomic number, this process appears to assemble the periodic table. As electrons fill orbitals of progressively higher energies, the theory completes the spotty, hypothetical, experimental grouping of chemical families of elements! The AOs did not arise from pure conjecture; we use them because they work in theory and in practice.

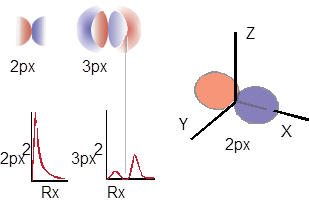
Figure B. Wavefunctions for px orbitals, N = 2 and N = 3. The graphs of px² below the AOs shows the probability of finding the electron (electron density) from the atomic center along the positive x axis. 2px has a planar node; 3px has a planar and a radial node. There is a 2p AO for the x, y and z directions and these all exist on the atom at the same time along with the 2s AO which gives us the octet rule. The occupancy of these orbitals also defines the number of valence electrons for the second-row elements.

I remember when I was first learning about AOs; one question I had was which direction is x? Does x point north or something? The direction of x is arbitrary. Mother Nature is not setting up orbitals. Orbitals are authored by people as parts of a mathematical model for the behavior of electrons. Whether they are real is probably a philosophical question. However, our choice of a direction for x, determines the direction for the other directional orbitals. The directions simply have to be ■ orthogonal. Both statistical and the directional definitions of orthogonal apply to atomic orbital theory. ■ Orbitron — maintained by Mark Winter at the University of Sheffield – is a site to tinker around with if you want to discover more about AOs.

For any orbital, the spin quantum number can be only +½ or −½. This means that any orbital describes the spatial population density of 0, 1, or 2 electrons, but no more than that. When 2px, 2py, 2pz, and 2s are occupied, the elements Li through F in the second row possess an octet. We understand the case in which the orbital is empty as a place that could be occupied by electrons during a chemical reaction. Like a trail through the forest in front of you, the unoccupied orbital defines the path that the chemical reaction can take. The interactions between occupied and unoccupied orbitals will be very important for us to understand chemical reactions. Some reactions are allowed by quantum mechanics and other reactions are forbidden. Without studying molecular orbital theory, you would be blind to this important aspect molecular reactivity.

2.2 MOLECULAR ORBITALS (MOs)

As alluded to in previous sections, organic chemistry is less the study of atoms, and more the study of molecules. We also focus on groups of atoms in molecules; we call these ■ functional groups. In short, organic chemistry is more interested in molecular orbitals (MOs) than AOs. We had to discuss the nature of AOs because we are going to construct MOs using AOs as Lego-like building blocks. This is a simplified approach; you’ll get a more rigorous introduction to the application of quantum mechanics to chemistry in more advanced classes. One might imagine that going from AOs to MOs is also going to require making atoms into molecules; it will define chemical bonding. In the following section we look at the simplest MO, in the H₂ σ bond, as an example of how AOs are used to make MOs and as a conceptual model for the single bond (σ) in organic molecules.

2.2.1 H Atoms ► Diatomic H₂

During early ■ inflation, the universe was opaque to light because it was too hot and dense for electrons to stick to protons. We should always try to structure our knowledge by explaining phenomena in terms of other known phenomena—this is in part the definition of science. How then do we understand a dark universe ‘in light’ of our initial definition of chemistry as emergent phenomena of the electromagnetic force? After the quarks condensed into ■ p+, the early universe at this stage was a dense, hot continuum of ■ e⁻ and p+. As such all distances between nuclei and electrons were present so the universe absorbed and emitted a broad continuum of light. The path that photons took through this early universe was very short, so the universe was dark.

With continued expansion at about 450,000 years after the Big Bang the continuum sea of electrons and p+ condensed to H atoms (H•) which formed H₂ quickly after that. This stage of universal evolution now allowed the passage of light because H• and H₂ absorb and emit light in a thin region in the ultraviolet part of the ■ EM spectrum.

Think about the universe going from opaque to translucent due to the condensation of electrons onto protons as if you are sitting in a boat in a foggy lake early in the morning. The fog is thinning, and as time passes you can see farther out over the water. But when we look at the universe today the farther out we look the farther back in time we look. Thus, we can’t use light to look beyond that time-distance barrier when the universe strongly absorbed all wavelengths of light. The big bang and everything for 450,000 years after it occurred is mysterious. The condensation of 2H• to H₂ was the very first time the universe did chemistry. The UV emission of excited H₂ molecules has been pulled to the longer microwave frequencies by the expanding universe. We can see this as residual EM noise—termed the cosmic microwave background (■ CMB). The AOs and MOs of H• and H₂ explain the ability to absorb and emit UV light and they determine the wavelength of this light. We will unpack this concept in the next sections.

From the discussion of AOs, you know what the AOs in the sequence above must have been, they were the 1s orbitals of the H atom. The process of converting AOs to MOs involves a linear combination of AOs. Remember from the section above, AOs can take on negative and positive values, but this is not electric charge. Just like a wave can ‘be’ at crest or trough, we can say that the negative values correspond to down and the positive values of the AO correspond to up. Just like a wave, when these up-down regions coincide they cancel each other out. The construction of the molecule involves adding two positive AOs (bonding) and adding a positive AO to a negative AO (antibonding). In this way we get two MOs from two AOs. The number of orbitals is conserved. The construction of molecules cannot destroy the potential of the starting atoms to contain electrons. A set of atoms can hold X number of electrons. We make a molecule from this set of atoms. The molecule has to be able to potentially hold X number of electrons. Like the AO, an MO can only contain two electrons. Thus, if we start with 2 AOs that can contain 2 electrons each we must produce two MOs that can in total contain 4 e⁻. In manipulations of orbitals the number of orbitals is conserved.

When you construct molecular orbitals from atomic orbitals the number of MOs you get must equal the number of AOs that you started with. Below I am representing the AOs and MOs as geometric solids but keep in mind that they are really radial distributions of electron density that is much greater when the distance to the nucleus is short.

For the 1s orbital you can’t tell the difference between this and this , these are the plus and minus phases of the 1s orbital. The signs of the AOs are different.

However, when you combine two orbitals to make the hydrogen molecule their differences are apparent because one possible combination produces destructive interference and installs a node where the sign of the new orbital changes, a region in which electrons can’t exist.

Destructive interference: ≡ This is the anti-bonding MO. The interference puts a planar node between the two atoms, a place where electrons cannot occupy. It does not matter whether we choose to represent the antibonding MO as shown or like this: , which is the result of multiplying the original MO by -1. We call a reproducible representation of because they are interconverted by multiplying by −1. They are considered to be the same orbital; the same container for electrons; you only have to show one of them and it doesn’t matter which one you show.

The other way to combine the two AOs leads to constructive interference: and we call this the bonding MO. Creating the bonding MO does not install a node between the two atoms; between the two atoms the sign of the MO does not change. Logically, just like the H atom 1s orbital, we cannot tell the difference between the MO shown and this phase unless there is another MO or AO to interact with it, thus, we can use either sign to represent the bonding MO. Because these MOs are just the result of multiplying by −1 these are also reducible representations of the MO for the hydrogen molecule. Since and are not converted to one another by multiplying by −1 they are referred to as irreducible representations of the MOs of H2. The number of electrons are also conserved in this AO-to-MO bond-making process; there are as many electrons in the final MOs as there were in the starting AOs. Due to the fact that one MO has a node and the other does not the two orbitals distribute occupied electrons differently. When molecules absorb light, an electron is promoted from a ground state orbital to a high-energy empty orbital. The electronic excited state of H2 has more electron density outside the σ bond (like σ* in Figure C) than does the ground state. If this kind of machinery did not exist there would be no photosynthesis or solar energy.

σ σ*

Figure C. Distribution of electron density in the σ (bond) and σ* (antibond--if it were occupied) of H₂. electrons = small black dots, nuclei = red dots. Nuclei would be too small to see; a nucleus scaled to golf-ball puts electron density ~8 mi away.

2.2.2 AOs and MOs Define Atomic and Molecular Size

Occupied orbitals both AOs and MOs define the size of atoms and molecules. Think about the content of the Figure C caption. If there is that much empty space between the electrons and the nuclei, why can’t molecules just pass through each other. Everything should be much more compressible. How can steel and diamond be so hard? Why can’t I walk right through the wall?

The fundamental reason why we cannot walk through walls and why steel is so hard goes back to the fact that only two electrons can occupy one orbital space at a time. This is the ■ Pauli Exclusion Principle and goes back to the fact that there are four sets of quantum numbers with the last one being only +½ or −½ for any orbital. It is therefore forbidden by quantum mechanics for one H₂ molecule to take up the space that another occupies because doing so equalizes these quantum numbers, so the two molecules bounce off each when they collide in the gas phase.

If we were to try to push two H₂ molecules together the energy of the system would abruptly increase. We call this steric interaction which gets unpacked in greater detail in the next couple chapters. The system is neutral so we cannot cite the repulsion between the same charges for the increase in energy. Similarly, we get steric interactions between two large groups on atoms, and this can destabilize molecules.

2.2.3 MO Energy Diagrams

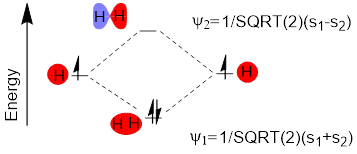
Figure D. An MO diagram for H₂. Interpret this diagram: As the two H atoms get closer, the energy of the electrons decreases, 2 AOs (half-filled) become 2 MOs one filled, and the other empty. The MOs are irreducible combinations of the AOs. Often these are called ψ1 and ψ2. The coefficient, 1/√2 is a normalization factor. Remember that the wave function squared will give the probability of finding the electron, this should = 1 when summed. When squared the coefficient ½ is distributed to the two parts of ψ1 and ½ + ½ = 1.

Molecular orbital energy diagrams are presented in terms of energy with the atomic components on the left and right and the molecular components in the middle. Using the H₂ MOs that we generated in the discussion above, we can present an MO diagram.

An energy axis and orbital conservation are essential components of the MO energy diagram. The bonding orbital for H2 is referred to as σ and the antibonding orbital as σ*. Alternatively, orbitals are distributed from lowest-energy to highest-energy and labelled ψ1 to ψn. The electrons lose energy in the bond making process. When orbitals are occupied in the MO energy diagram the corresponding energies are counted (thus, in the MO diagram for H2 above, the energy of ψ2 is not counted in the evaluation of the energy of the molecule because ψ2 is empty). In this case the energy of the two electrons decreases by 2x (E(ψ1) − E(1s)) or you can say that the energy of the system changes by −2E(ψ1) since the energy of the atomic fragments is usually taken to be zero. This energy change also defines the bond strength or the ■ bond dissociation energy (BDE) of the H2 molecule to be −2xE(ψ1) which is a positive number (It’s positive because 2xE(ψ1) is a negative value). The BDE is the energy required to break the bond between the two atoms in H2 into component H atoms. This is always a positive value because bond formation is defined by the electrons decreasing in energy as two atoms some together. In general BDE informs us about the stability of molecules.

Exercise 2.2.1 Click the BDE link and find the appropriate bond dissociation energy listed for H₂. Then label the energy of ψ₁ and ψ₂ on the energy axis in kJ/mol in Figure D.

2.2.4 Minimalist Summary of Bond Formation

1. AOs disappear and MOs form when atoms become molecules. Electrons are more stable in larger orbitals that are lower in energy. Remember that the larger AOs on the periodic table describe orbitals that are more distant from the nucleus and hence higher in energy than the AOs with smaller radii. Even though the MO is generally a larger orbital than the AO, there are two positive nuclear components stabilizing the MO instead of the one that stabilizes the AO.

2. The number of starting AOs = the number of MOs. This is orbital conservation.

3. Water runs down to the lowest point of potential energy, so do the electrons in MOs. Instead of occupying the high-energy σ* antibonding orbital the σ MO bonding orbital is preferentially occupied by the two valence electrons in H₂. There are no more electrons to fill the remaining σ* orbital.

4. Ultraviolet and in some cases visible light will promote electrons to antibonding orbitals. These electrons can do work and make higher-energy molecules. Basically, all food is made by solar energy.

5. The energies of only the occupied MOs are used to calculate the energy of the molecule.

6. The energy of the formation of H₂ from H atoms is negative, whereas breaking H₂ apart from molecule to its components is positive.

7. If we knew everything about the interactions of AOs to form MOs, we would know how stable the molecule is.

2.3 HYBRIDIZATION OF AOs TO DETERMINE MOLECULAR SHAPE

When we focused our attention on Lewis structures, we kept in mind that these structures were just a model of electrons in atoms and molecules. The Lewis structure falls short of capturing the behavior of molecules in many ways, but they are expedient tools for chemists to communicate about large molecules. Lewis structures miss much of the predictive power regarding shape and reactivity of molecules that molecular orbital models can capture.

In this section, we endeavor to build a theory for structure and reactivity of organic molecules. Below I give examples of how to frame the structure of the simplest ■ hydrocarbons in terms of hybrid orbitals: methane, and methane derived species, to build a foundation to conceptualize the σ bond in organic molecules.

2.3.1 Note to the Reader Regarding Sections 2.3, 2.6-2.8

Going deeper into the science for chemistry and engineering majors in part motivated writing this textbook. Also, some of our instructors felt that the usual textbook explanations of MO hybridization are disconnected from any useful ■ operational level for the student. We call these disconnected explanations ‘■ hand waving’, and when teaching, we try to avoid them as much as possible. These next sections operationally define MO hybridization, and the construction of directional bonds with hybrid atomic orbitals. The text tries to minimize the technical level, but retain enough details so operational, active learning is afforded to the student. Certainly, Organic Chemistry is easier to learn if you can grasp the fundamental concepts at an operational level, and frame what you learn next within an operational context. Understanding MOs at a level such that we can use them to understand structure and mechanism is the goal here. What you learn stays longer and you minimize study time.

Prerequisite Knowledge:

1. Mathematical definition of a vector.

2. Vector addition.

3. Compute the dot product of two vectors.

Students that do not feel comfortable with the math should read the summary below and skim the reading of these sections. A broad understanding of atomistic molecular geometry can be acquired.

Chemistry and engineering majors and other students more comfortable with the math will attain an operational level of MO hybridization from these sections and gain an appreciation for the distribution of orbital direction and orbital character in bonding schemes.

Summary:

• A hybrid AO (e.g. sp, sp², sp³) is a mixture of two or more AOs that inherits characteristic ■ directionality and energy from its component s and p AOs.

• After AO orbital mixing (hybridization), we use the new hybrid AOs to make bonds and antibonds in the same way that we used the 1s orbitals to make the bond and antibond in H₂. However the process is more complicated because there are more AOs, and some of these are directional. The next sections explain how one deals with these details.

• Hybridizing AOs conserves the number of AOs. For example, if we start with four AOs before the hybridization operation, we end with four new AOs after hybridization.

• The new hybrid orbitals get more spherical than the pure p orbital and tend to be more stable when occupied with electrons than the pure p orbitals. The hybrid orbitals inherit enhanced stability from the s AO.

• Because we use one s AO and 3 p AOs to construct molecules like methane (four bonds at the C atom), we refer to the four hybrid orbitals as sp³ orbitals at the C atom. At the H atom we will have 1s orbitals with which to form bonds.

• Since the s AO points in no particular direction, the spⁿ AO hybrids inherit their respective directions from their p AO components. Thus, the p AOs determine molecular geometry. The p AOs determine in which directions bonds point.

• An sp³ hybridization scheme at an atom points four σ bonds in 3D space equally. The sp³ orbital is a mixture of one s orbital and three p orbitals. Direction is distributed equally by the p orbitals and s character, and spherical shape is distributed equally by the fractional distribution of the s orbital.

• An sp² hybridization scheme at an atom points three σ bonds in 2D (coplanar) space equally. The atom has px, py and pz available to use in bonding. To construct this σ framework, it only uses two of the directional orbitals.

• Since electrons are more stable in s-like AOs, a hextet of electrons at an atom will have a pure unoccupied p orbital and three sp² hybrid orbitals. Methyl cation has a sextet of electrons around the C atom. CH₃⁺ is flat because electrons fill the MOs with s character at the C atom.

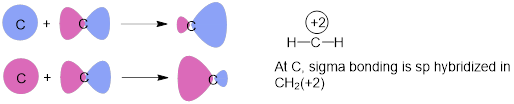
This is the same σ bond hybridization found in BeH₂.

• An sp hybridization scheme at an atom points 2 σ bonds in 1D (colinear in opposite directions).

• When you are asked about the hybridization of an atom what is actually being referred to are the σ bonds at the atom. A σ bond could be hybridized sp³ at one atom and hybridized sp² at the other atom. In a C−H bond the hybridization of the H atom is 1s; it is not mixed with any other orbital.

• Atoms in molecules move relative to each other. Due to mass differences, compared to the displacement of nuclei, electrons respond quickly. As CH₃⁺ oscillates around the ideal flat geometry by pyramidalizing with thermal motion, the σ bonding scheme goes from sp² to sp³ and back again.

The next sections show how orbital direction and character are operationally distributed in σ bonding schemes.

2.3.2 Methane: The Simplest Stable Hydrocarbon

Methane, CH₄, is the major component in natural gas and possessing only one C atom, it is the simplest hydrocarbon. In methane, the C atom is central, and all the C-H bonds are equivalent. The C atom has an octet and the H atom has a duet of electrons. Both of these elements have the electronic configurations of their nearest noble gas elements on the periodic table, Ne and He, respectively.

Think about bonding in methane given the considerations above. To achieve the octet, the C atom must use the four AOs of principle quantum number 2: 2s, 2px, 2py and 2pz. Mother Nature might have connected the three hydrogen atoms to C with the three 2p orbitals in an analogous manner to the way the H₂ molecule formed in the section above. The last H atom would then connect to the C atom with the 2s orbital. In this case, methane would have three H1s—C2p bonds and one H1s—C2s bond.

Since these p orbitals would point along the coordinate axes and since bonding should not change that orientation we might expect to get a structure (Figure E, left) that would have three H−C−H bond angles of 90° and three H−C−H ■ bond angles about 125.3°.

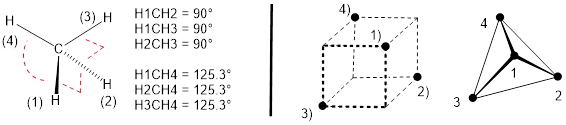
Figure E. (left) A hypothetical structure for methane using p orbitals and the s orbital to make C−H bonds with the expected bond angles. However, diffraction experiments indicate four CH bonds in methane distributed equally, occupying opposite corners of a cube. (right) Defining four planes with sets of three closest H atoms generates a tetrahedron, so this bonding pattern is referred to as tetrahedral.

All experimentation indicates that CH₄ is tetrahedral; there is not one H atom with more room in the atomic array like H(4) in Figure E (left) and three other H atoms crowded together with constricted bond angles like H(1), H(2), or H(3). The next sections explain how tetrahedral geometry arises naturally using the 2s, 2px, 2py and 2pz orbitals equally in bonding.

2.3.3 Hybridized Carbon AO Model for CH₄

There are a few ways to explain a symmetrical methane structure with s and p orbitals. In these MO models as long as the rules of orbital manipulation are obeyed and given that all four orbitals of N = 2 are used equally in the formation of each bond the resulting structure will be tetrahedral. This can be stated succinctly: as long as the 2s orbital is distributed equally to all four C−H bonds the structure will be symmetrical. In this case ¾ of each of the four orbitals would have to be p in character which means all three of the p orbitals are used equally. Here I present ■ Linus Pauling’s method of hybrid AOs to construct the MOs for methane.*

*Pauling, L., The Nature of the Chemical Bond. Application of Results Obtained from the Quantum Mechanics and from a Theory of Paramagnetic Susceptibility to the Structure of Molecules. J. Am. Chem. Soc. 1931, 53 (4), 1367-1400.

https://pubs.acs.org/doi/10.1021/ja01355a027

Note: Pauling refers to the hybridized AOs at C and the CH MOs in his original notation as ψ. The convention has changed. To clearly distinguish MOs from AOs, AO_C1 refers to the lowest-energy AO at the C atom, and ψ1 refers to the lowest-energy bond constructed from the AOs. Ψ2 refers to the second lowest-energy bond constructed etc. If you see ψ, it refers to the molecule. When the AOs or ψ MOs are equal energy (degenerate) these are numbered 1, 2, and 3 with px derived orbitals, prioritized over py, py has next priority then pz.

Let us follow Linus Pauling’s logic in his seminal 1931 paper about hybrid orbitals in the mixture of three Cartesian 2p orbitals and one 2s orbital at the C atom to make four equal, symmetric orbitals for the valence bond construction of methane with four H atoms. We expect four orbitals that explore the three Cartesian directions equally.

2.3.4 Shape of Hybrid Carbon AOs

When s orbitals mix with p orbitals, the new hybrids are more spherical. You can put this into operational terms by superimposing the s orbital on the p orbital and realizing that the same phases (same signs in the mathematical expression for the spatial distribution of electron density) add constructively and opposite phases obliterate each other. See Figure F wherein two irreducible representations of the combination of the input orbitals point in opposite directions.

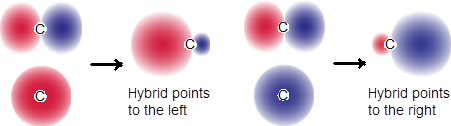
Figure F. Hybrids of s and p orbitals get directionality from p and roundness from s.

Here we added two orbitals together. The opposite signs destructively interfered whereas the same sign constructively interfered. This new set of AOs are irreducible representations because they were made from combinations of two orbitals and the two new orbitals are not interconverted by multiplication of −1. Orbitron referred to previously gives insight to hybridization in the ■ hybrid orbital section.

2.3.5 Directionality of Hybrid Carbon sp³ AOs

When s orbitals mix with p orbitals, the new hybrids inherit the direction of the p orbitals. When the three 2p orbitals and the 2s orbital are mixed, four new mathematical expressions (there must be four due to orbital conservation) that satisfy Schrodinger’s equation are generated and these new orbitals have p-like directionality pointed towards opposite corners of a cube to generate tetrahedral geometry. This occurs because the mixtures use px, py and pz bond vectors equally to generate the following AOs at the C atom.

AO(C)1 = 1/2 (s + px + py + pz) [1, 1, 1] AO(C)3 = 1/2 (s − px + py − pz) [−1, 1, −1]

AO(C)2 = 1/2 (s + px − py − pz) [1, −1, −1] AO(C)4 = 1/2 (s − px − py + pz) [−1, −1, 1]

Figure G. Pauling’s hybrid AOs at the C atom from irreducible representations of s and p combinations with directional vectors used. This is one subset of the four (tetrahedral) opposite corners of a cube; there is another in the remaining empty four corners.

In each case the positive s orbital is mixed with 1) positive px, py and pz; 2) a positive px and (negative py and pz); 3) a positive py and negative (px and pz); and 4) positive pz and (negative px and py) components. In this manner all orbitals are used equally, for example there are two negative and two positive contributions from 2px, likewise for 2py and 2pz in the set of four orbitals.

To follow the direction of orbital 1) (or Pauling’s ψ111; they are identical) above, we start from point (0,0,0) and draw a vector to point (1,1,1). Likewise following the direction in which orbital 2) is pointing, we start from (0,0,0) and draw a vector to (1,−1,−1). We can use the definition of the ■ dot product of two vectors to calculate the angle between these two vectors to be, Θ = acos(−1/3) = 109.47°…, an ■ irrational number. The angles associated with the dot products of any two AO vectors will equal exactly this number. This is the origin of the bond angle 109.5° that you learned about in general chemistry.

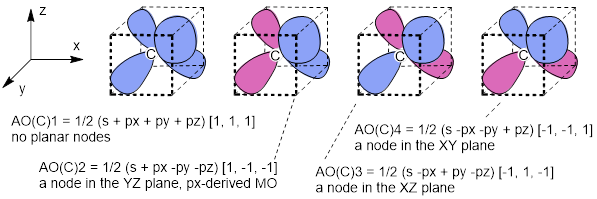
Figure H. Pauling’s C atom hybrid orbitals from s and p AOs are represented graphically. Planar nodes give the hybrid AOs directionality. AO_C1 has no planar nodes. AO_C2 changes sign in py, and pz putting a node at plane yz thus directed on the x axis. Sign changes in AO_C3 and AO_C4 also define planar nodes directing each on the y or z axes.

Exercise 2.3.1 Test your understanding. For these four AOs at the C atom to be distributed in space equally 2px, 2py and 2pz have to mix equally with 2s. In a manner shown in Figure F. Can 2px be mixed with 2py to obtain a hybrid orbital? Why or why not?

Exercise 2.3.2 Test your understanding. Build a set of sp² hybrid AOs starting with AO1 below.

AO(C)1ʹ = ½ (s −px −py −pz)

Exercise 2.3.3 Very challenging question designed to teach you instead of test yourself. Think about it a bit then read the answer. If instead of the left set of hybrid AOs below we had the set at right, what would be wrong with it?

AO(C)1 = ½ (s + px +py +pz) [1, 1, 1] AO(C)1’ = ½ (s + px +py +pz)

AO(C)2 = ½ (s + px −py −pz) [1,−1, −1] AO(C)2’ = ½ (s −px −py −pz)

AO(C)3 = ½ (s −px + py −pz) [−1, 1, −1] AO(C)3’ = ½ (s −px + py −pz)

AO(C)4 = ½ (s −px −py +pz) [−1, −1, 1] AO(C)4’ = ½ (s −px −py + pz)

2.3.6 Hybrid Carbon AOs + Hydrogen AOs ► CH₄ MOs

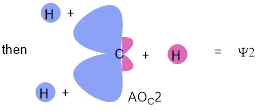
Now that we have set the hybridized AOs at the C atom, construction of the MOs for CH₄ is easy. We can summarize this construction in the MO energy diagram. For each of the C atom hybridized AOs that we developed above we make bonds to H atom 1s AOs without making any more nodes—we don’t change the sign across the CH connection. Sometimes there has to be a minus sign on the H atom 1s orbital (red) to match the sign on the C atom AO. Since there are four C atom AOs, we need to do this four times for the bonding MOs. We combined like phases of AOs to make the bonding orbital for H₂ shown in Figure D.

In a manner analogous to making the antibonding orbital for H2, the unoccupied, highest-energy orbital in H2, we make antibonding connections of H to C. In these the sign of the 1s H orbital is different to the sign of the AOC. This method produces MOs ψ5 – ψ8 in Figure I.

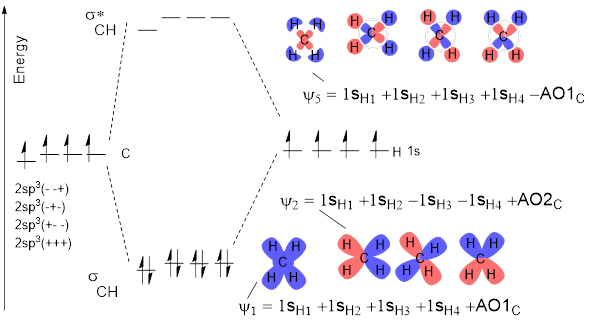
Figure I. An MO diagram for tetrahedral CH₄. Read this diagram as the three H atoms approaching the hybridized AOs of C to make bonds.

We had four hybridized AO_C’s and four 1s_H AOs; orbital conservation means we have to finish with eight ψ MO for CH₄. According to MO energy diagram convention, these are present in the middle of the diagram and are placed according to increasing energy on the vertical axis.

Exercise 2.3.4 The MO diagram in the figure above is incomplete. Given the convention in Figure H, label ψ₃, ψ₄, ψ₆, ψ₇, ψ₈.

2.3.7 Group sp³ Orbitals

In the section under this heading, we are officially beyond the scope of traditional content for Organic Chemistry 1 and 2, but at some point you may see group orbitals and you may wonder why you are not aware of them even though you were introduced to AOs and MOs of CH₄ in Organic Chemistry.

Remember that the 2s, 2p_x, 2p_y, 2p_z functions are already irreducible representations for atomic functions. There is no need to hybridize the AOs to make MOs in methane. Starting fresh from these s and p carbon AOs and hydrogen AOs, one can construct the methane MOs. The result is still three equivalent bonding MOs of the same energy and one that is just a little lower in energy due to having one less node. ψ₁ in Figure I is more stable than the ψ₂, ψ₃, and ψ₄ because it has no planar nodes (no phase changes at C) while the other three MOs have one planar node each. Also generated by this approach are the antibonding ψ5 – ψ8.

This alternate approach constructs a bonding and antibonding set of MOs called ■ group orbitals, which are officially outside the scope of introductory organic chemistry. Involved discussion of ■ group theory and mathematical symmetry operations are required to treat this topic justly. If your interest is piqued, stick with chemistry and you will see this in future coursework.

2.4 PES: EVIDENCE FOR CH₄ MOs

Photoemission spectroscopy (■ PES), (or photoelectron spectroscopy – same thing) requires ionizing X-ray electromagnetic radiation beyond the soft X-ray used in X-ray crystallography. Here the X-rays expel the electrons out of their bonding MOs. The x-axis corresponds to how tight the molecule holds the electron, the difference in energy between bound and free electrons (ΔE). The y-axis corresponds to the number of electrons ejected from this gas phase sample of CH4. The process involves measuring the energy of molecular ionization (CH4 à CH4+ + e−).

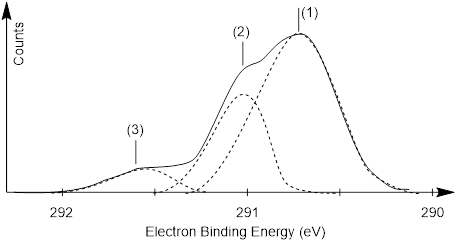
Figure J. Photoelectron spectrum of CH4_(g). (1) Patanen, M., Svensson, S., Mårtensson, N. Journal of Electron Spectroscopy and Related Phenomena, 2015, 200: 78-93. (2) Berrah, N.; Børve, K.; Bozek, J.; Carroll, T.; Hahne, J.; Kukk, E.; J Saethre, L.; Thomas, T., High-Resolution Carbon 1s Photoelectron Spectrum of Small Molecules. 2019. (drawn by A. Cammers)

In the PES of CH₄ above, the spectrum is broadened by bond vibrations, but curve deconvolution shows three energies of molecular ionization. The highest energy peak (3) corresponds to removing electrons from the 1s inner shell of the C atom. The more intense, lower-energy peaks (2) and (1) in the spectrum correspond to removing electrons from the valence shell. There are two peaks because there are two energy levels from which electrons come. We found these two energy levels in the valence shell with our theory above. Peak (2) corresponds to an electron coming from the more stable ψ₁ MO and peak (1) corresponds to an electron coming from ψ₂, ψ₃, and ψ₄. Since the electrons in ψ₁ are lower-energy (more stable) than the isoenergetic electrons in ψ₂, ψ₃, or ψ₄, ΔE for the ψ₁ electrons is greater than ΔE for ψ₂, ψ₃, or ψ₄ electrons.

Exercise 2.4.1 Does peak (1) in the spectrum above correspond to longer or shorter wavelengths of X-rays?

2.5 CH₄ ON THE MOVE

At this point we have an MO picture for the molecule of natural gas, CH₄. We can explain its symmetric structure observed in X-ray crystallography. We can explain the photoelectron spectrum with the sp³ MO picture of an s-derived MO and 3 p-derived MOs (planar nodes). However, what more can we do with this concept? How should we use the MO model of CH₄ to imagine methane?

Molecules and atoms move. Their movement defines the magnitude of the measurable conserved quantity, heat. The more molecular motion the higher the temperature. The heat, or kinetic energy of molecules in a sample, Q = CpT, where Cp is the heat capacity at constant pressure. We will unpack Cp in greater detail later but for now we just need to know that the H atoms relative to the C atom are vibrating on the order of 9E13 times/ sec or at 9E13 Hz. The model we developed above is for the symmetrical structure with all the bond lengths the same; however, these vibrations do not necessarily stretch all bonds at the same time and to the same extent. When a bond vibration breaks the symmetry of the structure, Mother Nature reworks the MOs on the fly—that’s right if you elongate a CH bond in methane the MOs are different because the tetrahedral symmetry is broken. This happens for two reasons: 1) electrons seek the lowest-energy state possible and 2) electrons readjust instantly to nuclear movement because at 9.1E−31 kg the electron is ~2000^th the mass of the proton at 1.7E−27 kg. Thus, the kinetic structure for methane has higher-energy MO representations oscillating around the low-energy electronic model developed above, like a pendulum oscillates about its rest state.

Next we use the MO model for CH₄ to understand other molecules. Before we talked about CH₄ we discussed the MOs of H₂, which provided a ladder on which to step up to CH₄. We will use the model of CH₄ likewise.

2.6 STRUCTURE OF THE METHYL ANION

The methyl anion, CH₃⁻, is a high-energy species that can be made, bottled and used to perform chemical reactions.

Exercise 2.6.1 Draw the bond-line structure of methyl anion, CH₃⁻.

Conceptually we can imagine removing H⁺ from CH₄ to get to methyl anion but when H⁺ is pushed away, what should change in the electronic description around the C atom? Both CH₃⁻ and CH₄ have 8 valence electrons so perhaps the electronic state of the two species is similar. Let’s follow the process of removing H⁺ with the concepts that we have so far.

2.6.1 MO Energy Diagram of the Methyl Anion

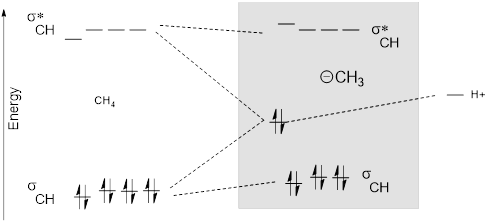
Figure K. An MO diagram for the removal of H⁺ from CH₄. One σ_CH and σ_CH* merge into a high-energy lone pair sp³ AO_C and an empty 1s orbital at H⁺, (orbital conservation; start with n orbitals, end with n orbitals). MO energy diagram for methyl anion is shaded region.

In the MO diagram above, the non-bonded electrons are high-energy because … well they are not bonded. Remember when we formed that bond from higher energy atomic orbitals, the energy of the electrons decreased, and this was the definition of bond formation. Breaking the bond reverses the process.

The MO of the lone pair takes more s character, and the σ_CH electrons take on a little more p character. This redistribution of hybridization decreases the three CH bond angles to little less than 109.5° and slightly increases the energy of σ_CH. Remember the s orbital stabilizes electrons better, and the electrons in σ_CH are stabilized by two nuclei whereas the lone pair is stabilized by only one. Rehybridization of the lone pair means that it doesn’t quite make it up to the atomic level.

Of course, the MOs above would not stay that we. We would have to find a way to separate the H⁺ from CH₃⁻; otherwise the tendency of electrons to lower their energy would just snap us back to the CH₄ with a large release of energy.

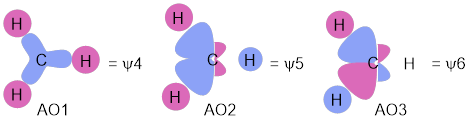
2.6.2 MOs of the Methyl Anion

The lowest energy MO has no nodes. The other color in the p-derived portion are small and hidden. When energy increases the orbitals don’t interact strongly, so often the lone pair is shown as an approximately an sp3 hybrid with the understanding that it has increased s character. So the methyl anion oscillates around an approximately tetrahedral structure.

Figure L. Hybrid MO model for methyl anion. From left to right energy increases.

2.7 STRUCTURE OF THE METHYL CATION

These descriptions are getting easier to do with the intellectual building blocks and the common vocabulary between us piling up for me to use in a plug and play fashion. We are obviously getting some return on our investment from the tedious attention to detail with CH4 above. The methyl cation behaves in a manner rather opposite to methyl anion. Imagine taking H− from CH4 to generate CH3+. We don’t have to ask how we generate this reactive species at this point. We are playing with concepts here and thinking about structure. Given our concepts above how should the structure change. Perhaps you should pause here and think about it briefly before you continue.

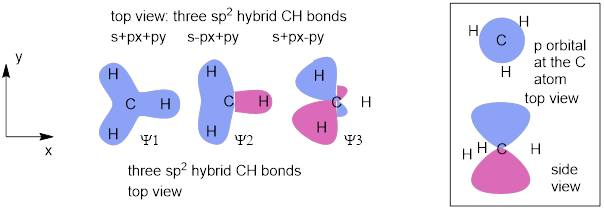
Figure M. Hybrid MO model for methyl cation. From left to right energy increases. This time the highest-energy orbital is unoccupied. The C atom as a hextet instead of an octet.

With only six electrons in the valence shell, one of the hybridized orbitals at the C atom is empty. What should happen to this empty orbital? Remember that the electrons seek to minimize their energy. The model we need to use to capture the behavior of methyl cation has to be a pure (non-hybridized) p orbital for the empty orbital.

The s character in the orbitals should be devoted entirely to stabilizing the bonded electrons. Let’s pick a direction, the z-axis, and say that pz is empty. This means that the z direction is not explored by the rest of the bonded hybridized orbitals and the CHHH connections use s, px, and py orbitals equally. The bonds at the C atom are now sp² hybridized because they consist of two 2p orbitals and one 2s orbital. Electrons seeking s character drive the structure flat.

What about those bond angles? How should rehybridization of the bonded σ electrons affect the HCH bond angle? There are many different ways to do this that give the same answer. I’ll give you one. Let’s leave one MO along the x-axis. This orbital is ⅓ s and ⅔ px because it is sp² which means 1 part s and 2 parts p. Since the orbital lies on the x-axis it has no py component. We can name this orbital AO_C1. Let us look at this in greater detail.

2.7.1 Directionality of Hybrid Carbon sp² AOs

When s orbitals mix with p orbitals, the new hybrids inherit the direction of the p orbitals. When the two 2p orbitals and the 2s orbital are mixed, three new mathematical expressions (there must be three due to orbital conservation) that satisfy Schrodinger’s equation are generated and these new orbitals have p-like directionality but can only lie on a plane because the last 2p orbital is not mixed to form bonds.

When we did this for methane to generate tetrahedral geometry, we pointed the vectors of the sp³ hybrid AOs toward the four opposite corners of the 3D cartesian system. We found we could use 1’s to get around this coordinate system. When we add the vector contributions together, we see that they all pull in opposite directions for a sum of [0, 0, 0], and, of course, with a two negative and two positive contributions from px, py and pz, they all participate equally.

AO(C)1 = ½ (s + px +py +pz) [1, 1, 1]

AO(C)2 = ½ (s + px −py −pz) [1,−1, −1]

AO(C)3 = ½ (s −px + py −pz) [−1, 1, −1]

AO(C)4 = ½ (s −px −py +pz) [−1, −1, 1]

--------------

[0, 0, 0]

When we try to use 1’s to distribute three vectors in 2D we are not rewarded with similar success.

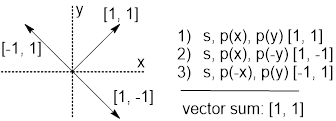
Figure N. When we try to use 1’s to distribute p bond vectors in 2D, it does not work.

The vector sum is [1, 1] not [0, 0]. Vectors [−1, 1] and [1, −1] cancel, but [1, 1] remains, so this bonding array is not symmetrically disposed in 2D. This non-zero vector sum means that the p orbitals are not all used equivalently. Which means that CH bond angles = 90, 90 and 180° when the CH bonds and antibonds are constructed.

The figure above fixes the problems in the previous figure. From these vectors, we can layout an sp² bonding array in the XY plane, because the pz orbital is not involved in the hybridization of the bonding MOs. Let’s just leave the first C atom, AO_C1, on the x-axis; we could rotate it anywhere in polar coordinates, but it’s probably easier to do it this way. There is something else that we have to fix. This AO_C1 is not all px; it needs coefficients √⅓s and √⅔p to reflect the fact that it has ⅓ s character. Remember that when we are looking for electrons these coefficients will be squared and ⅓ + ⅔ = 1 which means we have 100% chance of finding the electrons.

This also means that there is only ⅓ px to distribute to AO_C2 and AO_C3 since there are two hybridized AOs in which to put px and px is evenly distributed according to the vector picture, the coefficients for px in these are −√(1/6). Since AO_C2 and AO_C3 are both ⅓s and 1/6px the coefficient for py must be ½ since ⅓ + 1/6 = ½, we another ½ to equal 1.

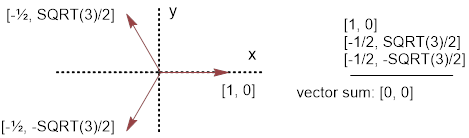
Figure O. Coordinates that distribute p directionality equally in three hybrid AO_Cs.

AO_C1 = √(⅓)s +√(⅔)px: [1, 0]; AO_C1 is 33.3% s and 66.7% p and 0% py. There is 100% py and 33.3% px to distribute to the other two hybridized orbitals.

AO_C2 = √(⅓)s −√(1/6)px +√(½)py: [−½, √(3) /2]; At 1/6 or 16.7% px, which means this AO is distributed equally between hybridized AO_C2 and AO_C3, ⅓s + 1/6px (sums to 3/6 = 1/2 ) means that the remaining py portion must be ½ to complete hybridized AO_C2.

AO_C3 = √(⅓)s −√(1/6)px −√(½)py [−½,, −SQRT√(3) /2]

Note: Just like we kept one 1s orbital in the same phase and we included +1 and −1 contributions from the other 1s orbital in the construction of σ and σ* in H2, here we keep the 2s orbital in the same phase and we included +1 and −1 contributions from the px, py and pz orbitals. The distribution of p-orbital direction here complicates construction, but other than that, the H2-building process and the CH3 building process are the same.

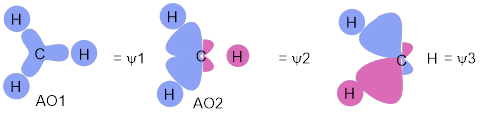
The lowest-energy valence hybrid orbital has positive contributions from the 2s, 2px and 2py AOs and it bonds with three H1s AOs; that’s MO ψ1 in Figure M. ψ2 in Figure M is MO 2): s, p(−x) + three H1s AOs this is shown below.

The negative sign on px in C atom AO_C2 for CH₃⁺ means that there is a node at the line x = 0; the positive sign on py in AO_C2 for CH₃⁺ means that there is not a node on the line y = 0. This negative sign on px in AO_C2 for CH₃⁺ has the same meaning as the negative signs in AO_C2 of CH₄ (Figure H). AO_C2 in CH₄, has −py, and −pz putting a node in the YZ plane of that AO. Can you find the node in AO_C2 for CH₃⁺ above?

Similar construction gives us the following orbital for AOC3 for CH3+ wherein −px, −py mean that the sign of AOC3 must change as you cross the y axis (x = 0) and as you cross the x axis (y = 0).

AO_C3 = √(⅓)s −√(1/6)px −√(½)py [−½,, −√(3) /2]

Exercise 2.7.1 Test your understanding. Look at AO_C3 above. Now look at the CH ψ3 MO in methyl cation in Figure M. This MO has two CH bonding interactions and one CH non-bonding interaction. Why is the CH interaction non-bonding?

Exercise 2.7.2 Hopefully, you realize that Figure M is incomplete. How many MOs according to MO conservation should be in the diagram? How are they arranged on the energy axis in the complete MO diagram?

Hint: How many AOs did we start with and how many AOs and MOs are shown in Figure M? Look at the MO diagram for CH₄. What’s missing?

Hint: How did we make the MOs of methane after we setup the hybridized C atom AOs? Follow that method as an example.

Exercise 2.7.3 Use the dot product to confirm that bond vectors [1, 0], [−½, −√(3) /2] and [−½,, −√(3) /2] have 120° between them.

2.8 STRUCTURE OF THE METHYL RADICAL

Given the terrain that we’ve covered it is getting a lot easier to talk about new topics in organic chemistry. Methyl radical has an odd number of electrons. To get there with a thought experiment imagine breaking one of the CH bonds of methane and generating •CH₃ and •H. To generate methyl anion, we took off H⁺; to generate methyl cation, we took off H⁻ (hydride). This time we are nabbing the hydrogen atom. As the title of the subsection indicates methyl with no descriptors refers to •CH₃; that’s what ‘yl’ means.

Methyl is somewhere between two extremes that we have already discussed, a C atom bound to 3 H atoms with an empty orbital and the same assembly with an occupied orbital. However, it is decidedly closer in structure to CH₃⁺. There is something very compelling to Mother Nature about filled atomic valence shells; half empty just doesn’t even half satisfy her. Everything we said about CH₃⁺ in terms of orbitals applies broadly to •CH₃. However, to compare these structures we must define an atomic parameter.

2.8.1 THE IMPROPER DIHEDRAL ANGLE

We referred to atomic parameters earlier. A common one is bond length which is the lowest-energy distance between two nuclear centers in a bond. Bond stretch and contract about this distance like a pendulum repeatedly swings through its lowest point. At the high point pendula store potential energy; at the low point velocity is maximum and all the potential energy converted to kinetic energy. Similar phenomena occur with bond angles with a scissoring motion. The two other atomic parameters important for molecular motion are the dihedral angles.

Figure P. Bonds vibrate very quickly.

Figure Q. Scissoring motion occurs with bond angles.

Figure R. Inversion, a motion tracked with the improper dihedral angle.

The bond length is a two-atom parameter. Just measure the distance between two atoms. The bond angle is a three-atom parameter because the relative positions of all three atoms are necessary to determine the bond angle.

Dihedral angles are angular distances measured between two planes. We’ll discuss proper dihedral angles later. The reason for the word improper is the fact that this four-atom parameter the angle between a plane and an infinite number of planes instead of just one. We could measure the improper dihedral between the plane formed by atom 1, 2 and 3 and the infinite set of planes passing through the bond vector defined by atoms 2, and 4. The dihedral angle changes as the methyl anion goes from pyramidal to flat to pyramidal again. When flat the improper dihedral angle is usually defined as zero and deviations from planarity accompany increasing numbers.

At this point we can predict what the shape of the potential energy curves will look like for methyl cation and anion. Or at least when I show them to you it will immediately make sense.

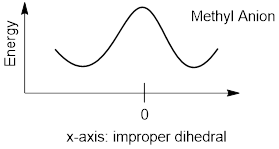
Figure R. Inversion, a motion tracked with the improper dihedral angle.

The potential energy for methyl cation is lowest at an improper dihedral angle of 0° where that of the methyl anion is highest at improper dihedral angle equal zero. These two unstable molecules (they quickly react with other molecules) oscillate around different stable states. We can rationalize this behavior from what we have discussed.

The flat cation puts electrons in MOs with the most s character that it can find. These are sp², and as we discussed, the C atom with the bonding orbitals thus hybridized sp² only has two dimensions to explore. The only other orbital that explores the 3^rd dimension is the last p orbital which is better left empty. In normal thermal motion involving changes in improper dihedral angle the potential energy must go up because the molecule is no longer planer, and this means that all three p orbitals must me involved in bonding. The C atom is no longer sp²; it transitions smoothly to some other spⁿ hybrid with n > 2 and less than 3. Rehybridization happens instantly with changes in molecular shape.

On the other hand, the methyl anion has the flat structure as the high point. When the methyl anion is flat the non-hybridized p orbital has a pair of electrons. However, these electrons are more stable in an MO that has s character. The geometries of these molecules are such that they are for the same reason.

2.9 COMUPUTATIONAL CHEMISTRY

Organic chemists often use computational chemistry to understand chemical reactions or how a molecule may be interacting with another molecule, for example a molecule in an enzyme active site. Organic chemistry uses computation to interpret crystal structures in terms of molecular interactions. Much of what we know about molecules comes from the interaction of molecules and light (electromagnetic radiation). The theory about how to interpret that interaction into molecular geometry and reactivity is largely the stuff of computational chemistry.

The ability to compute molecular structure and properties of molecules like oxidation potential, bond strengths, and at what wavelength a molecule will absorb light has evolved with the evolution of the computer. The kinds of answers that immediately come out of an algorithm to capture molecular properties are the energies of MOs, and how the MOs look. Atomic parameters also result from calculations: bond lengths, bond angles, and bond dihedral angles in molecules.

Understanding MOs at some fundamental level, like the abbreviated fundamental perspective introduced in this chapter will allow you to make some sense out of higher-level MO calculations. Aspects of MO conservation and symmetry; knowing that molecules have antibonds and knowing how they interact with bonds (we will unpack that next) will make you literate regarding the output of computation.

KEY TO CHAPTER 2 EXERCISES

(Arthur Cammers, 2019)

Exercise 2.2.1 Answer: −218 and +218 kJ/mol

More important than getting the problem correct is the question: Can you explain how to calculate these numbers?

Exercise 2.3.1 Answer: To mix the AOs must overlap. However, 2px and 2py are orthogonal. Disposed 90° apart they do not overlap. The planar node of one orbital passes through the region of greatest electron density of the other.

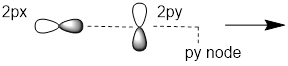
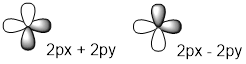
When linear combinations of orthogonal orbitals are mixed such as px and py, no new direction or shape results. Thus, distributing s character equally throughout the four orbitals means tetrahedral symmetry in orbital direction. Each orbital must be 1 part s and 3 parts p; this kind of hybridization is called sp³.

Exercise 2.3.2 Answer: Given above at [−1, −1, −1] is just the p orbital vector of AO(C)1 multiplied by −1. Multiply the rest of the original three p orbital vectors by −1.

−1 x [1, −1, −1]

Thus,

AO(C)2ʹ = 1/2 (−s −px +py +pz)

AO(C)3ʹ = ½ (s +px −py −pz)

AO(C)4ʹ = ½ (s +px +py −pz)

This hybridized set is the other tetrahedron inscribed by the cartesian cube with the first orbital vector at [−1, −1, −1]. There is nothing wrong with starting out this way. Choosing AO1) the way we did means we have to choose different vectors for AO2, AO3 and AO4 to use the p AOs equally. Given the standard way to represent the x, y, z Cartesian coordinates. Graphically the original set of sp³ orbitals below changes to the one on the right when you start with s, p(−x), p(−y), p(−z) [−1, −1, −1].

If you start with AO(C)1ʹʹ = ½ (−s −px −py −pz), this new hybridized sp3 orbital set would have the same directionality as the original AO(C)1 = ½ (s +px +py +pz), except we’d have to color it red (negative) in Figure H instead of blue (positive).

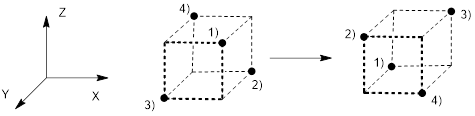
Exercise 2.3.3 Answer: The new set of AOs does not describe a tetrahedral bonding array, because AO(C)1’ = ½ (s + px +py +pz) [1, 1, 1] is pointing 180° away, in the opposite direction of AO(C)2’, [−1, −1,  −1,] but what is wrong with that?

The initial task was to use the 2p orbitals equally. When we sum the p orbital vectors of AO(C)1, AO(C)2, AO(C)3, and AO(C)4, we get [0, 0, 0]

[1, 1, 1] +

[1, −1, −1] +

[−1, 1, −1] +

[−1, −1, 1] +

----------------

[0, 0, 0] which means the p directionality is equally distributed.

When we sum the p orbital vectors of AO(C)1’, AO(C)2’, AO(C)3’, and Ψ4’ we get [−2, 0, 0]

[1, 1, 1] +

[−1, −1, −1] +

[−1, 1, −1] +

[−1, −1, 1] +

----------------

[−2, 0, 0] - a vector on the x-axis, meaning the p directionality is unequally distributed.

Exercise 2.3.4 Answer:

ψ₃ = 1s_H1 − 1s_H2 + 1s_H3 − 1s_H4 + AO3_C, ψ₄ = 1s_H1 − 1s_H2 − 1s_H3 + 1s_H4 + AO4_C

ψ₆ = 1s_H1 + 1s_H2 − 1s_H3 − 1s_H4 − AO4_C, ψ₇ = 1s_H1 − 1s_H2 + 1s_H3 − 1s_H4 − AO3_C

ψ₈ = 1s_H1 − 1s_H2 − 1s_H3 + 1s_H4 − AO4_C

Exercise 2.4.1 Answer: The lower energy peaks correspond to longer wavelengths. ΔE = hv = hc /λ. ΔE and λ have an inverse relationship.

Exercise 2.6.1 Answer:

The number of electrons in the structure = 4 + 3x1 +1 = 8.

Electrons used in bonds = 6.

Electrons in lone pair = 2

Formal charge at the C atom = FC = 4 – 6/2 −2 = −1

Exercise 2.7.1 Answer: In AO_C3 there is a node on the line y = 0 about which the wave function signs change. This means that you cannot choose a sign for AO H1s that makes a bonding or an antibonding interaction; the interaction is intermediate between bonding and antibonding. See illustration below.

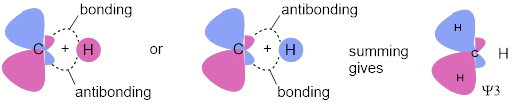
Antibonding + bonding = non-bonding, literally … do it … add the two representations above of ψ3 MO together and you get the ψ3 MO shown in Figure M. The red on one H and the blue on the other cancel to give you the picture of ψ3 shown in Figure M.

Exercise 2.7.2 Answer: There are three antibonding MOs missing. To make these combine the H atom 1s AOs in an antibonding fashion with the three C atom hybrid AOs. To make the bonding MOs in Figure M we combined the C atom hybrid AOs with H1s AOs in a bonding fashion as below

To get the antibonding MOs,

To arrange the ψ1- ψ6 in energy realize that ψ1 has no planar or spherical nodes. Whereas ψ2 and ψ3 have a planar node each; ψ4 has a spherical node but no planar nodes; and ψ5 and ψ6 have a planar node and a spherical node each. Remember that like signs produce bonding interactions and different signs of interacting AOs make antibonding interactions which increase the energy of the electron that populates the MO.

Exercise 2.7.3 Answer:

The dot product of two vectors: [x1, y1] and [x2, y2] is defined as

(x1•x2 + y1•y2) /{√(x1² + y1²)•√(x2² + y2²) = acos

Plugging the numbers for the first pair gives

−½/ √(1 + 0)•(( −½)² + √(¾)² = −½/ 1 = acos(−½) = 120°

You have a calculator that has options of radians and degrees. Make sure this is set on degrees. If you compute the angle in radians you must multiply by 180° / π to get the answer in degrees.

CHAPTER 2 PRACTICE PROBLEMS

(Arthur Cammers, 2019)

Hint for the following problems. Chemistry about electrons and less about number of protons or mass or nuclei. You don’t have to know the answers or even get them right to use the correct logic in your answer.

PP 2-01 Draw the line structure of BH₃. How are the BH σ bonds hybridized? What is the geometry of the BH₃ molecule? Why does the BH₃ molecule have this geometry?

PP 2-02 Draw the line structure of NH₃. How are the NH σ bonds hybridized? What is the geometry of the NH₃ molecule? Why does the NH₃ molecule have this geometry?

PP 2-03 Draw the line structure of BH₄⁻. How are the BH σ bonds hybridized? What is the geometry of the BH₃ molecule? Why does the BH₄⁻ molecule have this geometry?

PP 2-04 Draw the line structure of BeH₂. How are the BeH σ bonds hybridized? What is the H−Be−H bond angle of the BeH₂ molecule? Why does the BeH₂ molecule have this bond angle?

PP 2-05 In a diagram show how the energy of BeH₂ changes with thermal motion in the H−Be−H bond angle. See examples in Figure R.

PP 2-06 Show the MOs of NH₃. How are these different from CH₃⁻? How does electronegativity affect the energies of MOs?

PP 2-07 Show the MOs of N(CH₃)₃. Don’t worry about defining the MOs of the CH bonds in CH₃ groups just focus on the MOs at the N atom and pretend •CH₃ bonds are simply to N as •H. How does this structure compare to NH₃ in terms of geometry?

PP 2-08 Think about the concept of electronegativity. Can bonds and orbitals possess electronegativity? Electronegativity is just an expression of how tightly something elemental holds electrons. Bonds at atoms, AOs and MOs should be even more ■ elemental (definition 2) than atomic elements themselves. Given this perspective, which is more electronegative an sp³ hybrid AO or a sp² hybrid AO?

PP 2-09 How should the OH bonds in water be hybridized to a first approximation? What about correcting your first answer a little? You expect the distribution of s character to be the same to both lone pair and σ bond at the O atom? How should it differ? How does this distribution of s character affect the HOH bond angle?

KEY TO CHAPTER 2 PRACTICE PROBLEMS

(Arthur Cammers, 2019)

PP 2-01 Answer:

There is an empty orbital at B. The six electrons in the hextet seek s character so the empty orbital is pure p. There are two p orbitals and one s orbital to make three σ bonds so the BH bonds are hybridized sp² at B. The bonding array uses only 2 directional orbitals therefore the bonds are confined to 2D space. The geometry of BH₃ is trigonal planar. The electrons are more stable in orbitals with s character, so the vacant site is pure p. In that case the molecule must be flat.

PP 2-02 Answer:

The eight electrons in the octet around the N atom seek s character so they distribute it almost equally in four orbitals, 3 σ bonds at N and a lone pair all hybridized sp³. Three directional orbitals are used equally so the molecule is pyramidal. The molecule has this geometry because electrons are more stable in orbitals with s character.

PP 2-03 Answer:

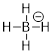
The eight electrons in the octet around the B atom seek s character so they distribute it almost equally in four orbitals, 3 σ bonds at B and a lone pair all sp³ hybridized. Three directional orbitals are used equally so the molecule is tetrahedral. The molecule has this geometry because electrons are more stable in orbitals with s character.

PP 2-04 Answer:

There are two empty orbitals at Be. The four electrons on Be seek s character so two empty orbitals are pure p orbital. One p orbital and one s orbital make two σ bonds, so the BeH bonds are sp hybridized at Be. The sp hybridization means that the molecule can only bond on one directional axis since one directional orbital is used to make these bonds. The molecule has this linear geometry because electrons are more stable in orbitals with s character.

PP 2-05 Answer:

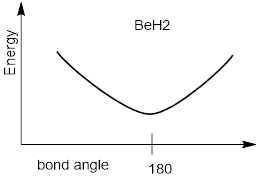
PP 2-06 Answer:

Part of the learning objective in this chapter was the realization that isoelectronic structures have the same MOs. The electronegativity of the N atom decreases the energies of these MO but does not change the shape. The methyl anion is much more basic than NH3 due to less electronegative in the C atom than the N atom.

PP 2-07 Answer:

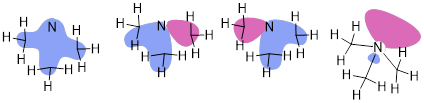
PP 2-08 Answer: We are talking about pulling the e- out of an atomic orbital. The greater fractional s content in the AO will make it more electronegative. The sp2 hybrid AOs?

PP 2-09 Answer: As in NH₃, to a first approximation the hybridization at the O atom in water is sp³, but the lone pairs should want more s character and the bonded pair should settle for less because the bonded pair has two nuclei stabilizing the electrons. This effect should decrease the bond angle a bit from 109.5°.