CHAPTER 3. UNDERSTANDING sigma AND pi BONDING

(Arthur Cammers, Ashley Jolly Steelman, and Susan Odom, University of Kentucky, 2019, with excerpts from Timothy Soderberg, University of Minnesota Morris, “Organic Chemistry with a Biological Emphasis,” 2016)

Note: Normally px, py and pz have subscripts and are written as p_x, p_y and p_z; here the author dropped the subscripts for better readability.

Learning Objectives:

1. Explain how Pauli Exclusion requires σ and π bonds. ■■

2. Appreciate the energetic differences between σ and π bonds. ■■

3. Explain the local nature of σ and the global nature of π bonds as well as how electrons in p orbitals and π bonds conjugate. Know why σ bonds do not do this well. Know how this difference in behavior relates to the variability in energy with structure of σ and π.

4. Understand the relationship between s character, p character, and conjugation in the determination of molecular geometry and energetically stable conformation.

5. Understand how conjugation affects orbital energy. ■■

6. Understand how a point of saturation between two π systems affect MO conjugation.

7. Count the electrons in a π system given the line structure of a molecule. ■■

8. Build π MOs of unsaturated molecules and use π MOs to predict chemical reactivity. ■■

9. Make a good guess at what the π MOs look like for a conjugated molecule.

10. Identify the hybridization at atoms and the types of orbitals used to form bonds and house electron lone pairs.

11. Count (unhybridized) p orbitals at atoms and parse this count into molecular geometry and /or reactivity. ■■

12. Realize that atoms in molecules are always moving relative to each other. Realize that hybridization changes instantly with this internal motion. Realize that when asked about the hybridization of an atom what is really being asked is: What is the hybridization of the orbital(s) (probably σ bond, or lone pair) at the atom in the lowest-energy conformation of the molecule.

13. Relate hybridization of lone pairs to their reactivity. ■■

14. Draw MO energy diagrams for molecules with σ and π bonds.

15. Understand the origin of energetic barriers to bond rotation. Be able to explain why σ bonds rotate and π bonds do not.

16. Draw changes in the MO energy diagram of a π bond as a function of dihedral angle. ■■

17. Explain why π bond rotation leads to a new molecule and σ bond rotation does not.

18. Know how polarity affects the properties of molecular substances.

19. Explain what we mean by the bulk properties of substances and which molecular characteristics gives rise to bulk properties and the origin of these molecular characteristics. ■■

20. Explain the effect of atomic electronegativity on the properties of substances.

21. Calculate a dipole moment given a charge separation for a certain distance.

22. Define the Debye unit operationally. ■■

23. Describe the phenomenon of UV–visible spectroscopy.

24. Describe how structural changes in molecules affect the UV-vis spectra. ■■

25. State why we are talking about UV-vis spectroscopy in this chapter and how the subjects are related.

26. Explain how two occupied orbitals interact. Explain how an occupied orbital interacts with an unoccupied orbital and why this concept is important to chemistry in terms of conformational distribution and bonding. ■■

3.0 INTRODUCTION

(Arthur Cammers, 2019) (Image: Molecular Models of C₂H₆, C₂H₄, and C₂H₂, Arthur Cammers)

This chapter addresses π bonding and how it interplays with σ bonding in organic structure. The orbital hybridization theme from the previous chapter is necessary because as the number of π bonds increases at an atom, the s orbital character of the bonds must also increase. The reader should think back on the general anatomy of these spn hybrids from the previous chapter as these themes come up. Nearly all organic molecules, even highly reactive molecules, can be rationalized through the prism of hybridization in terms of structure and reactivity. Geometry, bond length, pKa, and as we will see in coming chapters, many other properties unify under the hybridization argument. To determine molecular geometry, one should try to understand the argument instead of recurring to mnemonic tricks—which can be beguiling when learning something new and complex. Groundwork and foundation is being laid here. If you can understand what is going on now, there will be less to memorize later.

Here we broaden the argument of π bonding to include parallel interactions between σ bonds and unoccupied MOs. These aspects of MO interaction will be useful for the discussion of conformation and molecular stability of alkanes, cations and radicals in the following chapters. This chapter also addresses the polar nature of π bonds and the changes that occur to π MO systems with conjugation. Naturally the discussion turns to the properties of molecular substances as a function of molecular interactions. As with previous chapters that include epistemological aspects, this chapter discusses the pertinent experimental technique that measures π bonding in molecules: UV-vis spectroscopy.

3.1 ATOMIC ORBITALS (AOs)

(Arthur Cammers, 2019)

In the preceding chapter we considered methane, the simplest of hydrocarbons, and we considered related species, realizing that there are many related structures to which we can apply the methane MOs. As is most often the case, the application of theories does not scale infinitely, and when we move on to ethane, H₃C−CH₃, we will; put together •CH₃ and will not worry much about the angles of H−C−C versus H−C−H and so on. In other words, what we build will not be good enough to explain the photoelectron spectrum (PES) of ethane, but it will be good enough to understand the major concepts we cover in this course.

Here we use: (1) the concept of the σ bond; (2) the concept of sp³ hybrid MOs at each C atom without the details that we developed previously for methane; (3) the geometry that sp³ hybrids set for the bond angles; (4) a reminder that chemically, •CH₃ bonding with •CH₃ looks like •CH₃ bonding with •H; and (5) knowing that the overall construct of the MO energy diagram is analogous to H₂. We are building a theory that we can use like ■ Legos^TM to address chemical structure and reactivity.

Figure A. Simple MO diagram for CH₃−CH₃.

The obvious differences between bonding in H₂, bonding in CH₄ and forming the C−C σ bond in C₂H₆, are that two sp³ hybrids interact in a directional fashion, head-on (as in a head-on collision between two automobiles), instead of the non-directional manner of two 1s_H orbitals in H₂. Also, the interaction makes σ_CC and σ_CC*, which are analogous but not equivalent to σ_CH and σ_CH* MOs in the molecule. For simplicity, σ_CH MOs are shown in bond-line structure format.

In Figure A, notice that line between the two C atoms is not depicted because the line represents a σ bond. The occupied MO is another way of representing the bond between the C atoms. Therefore, including both the line between the C atoms and the MO would be redundant.

3.1.1 The σ Bond in Ethane Rotates

The σ bond in H₂ probably rotates, but there is no way to know for sure. However, molecular groups attached by σ bonds rotate internally as part of normal thermal motion; we know that for sure. These changes are tracked by dihedral angles. In this the atomic parameter is the proper dihedral angle; proper because it is defined by only two planes. Look back to the last chapter at the improper dihedral angle and why it was called improper.

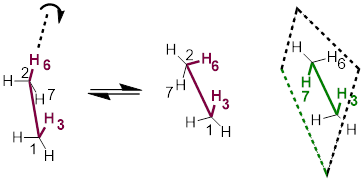
Figure B. Conformations arise when single bonds rotate, tracked by 4-atom dihedral angles.

The convention in bond-line structures for perspective views is whatever appears lower is closer to the reader. In Figure B, in the leftmost structure, C1 is closer to you than is C2, and the plane defined by atoms H3, C1, and C2 coincides with the plane defined by C1, C2, and H6. When these two 3-atom planes coincide, the H3-C1-C2-H6 dihedral angle = 0°. In the middle structure in the figure, H3-C1-C2-H6 dihedral angle has changed by ~60° compared to the original structure, and the H3-C1-C2-H7 dihedral angle has a value of 180°.

To connect the leftmost structure and the middle structure in the figure, we need an equilibrium arrow because atoms are moving (they are not resonance structures) and the energies of these structures differ by 12.1 kJ/mol. This is a very small number because it corresponds to a barrier to rotation, and the H6 makes it around to the start about 30 billion times per second (■ Hz) at room temperature!

3.1.2 Molecules with Rotatable Bonds Related to Ethane

By logical extrapolation one would expect longer-chain hydrocarbons to shape-shift very quickly at ~25 °C. We might expect Mother Nature to madly play with octane like the most addictive fidget spinner on the planet as in Figure C below. Furthermore, other atoms in the chain connected by single bonds should likewise rotate and change the shape of the molecule, e.g. CH3CH2CH2CH2SiCl2CH2OCH3. This text will give this issue more attention when it addresses the topic of molecular conformation: molecular shape. For now, we just need the concept of σ bonds as rotors to contrast them to π bonds, reminding ourselves that π bonds do not rotate at room temperature.

Figure C. Single bonds rotate and change the shape of the molecules with time.

3.1.3 Naming Alkanes

Straight chain alkanes are simply named by the number of carbons in their chain.

For effective communication, you must memorize some names of chains, substituents, and functional groups. For this chapter, the following list is important.

Memorize the following names of the alkane chains.

· methane

· ethane

· propane

· butane

· pentane (mnemonic: pentagon)

· hexane (mnemonic: hexagon)

· heptane

· octagon (mnemonic: octagon)

· nonane (mnemonic: nine)

· decane (mnemonic decade)

3.2 Structure of Ethylene: the Non-Rotatable π Bond

(Arthur Cammers, 2019)

When we first discussed depicting molecules with bond-line structures, there was some mention of double bonds – that they consisted of a σ bond and a π bond – but that is as detailed as it got. When looking at the double bond connection on the MO level of resolution, one can’t get away with simply considering the double bond as four electrons in a bond. Furthermore, the details of the double bond unveiled by the MO perspective inform how we parse line structures into chemical relevance.

The neutral structure ethylene, C2H4, has one degree of unsaturation, and as such has a double bond. We should be able to put the two halves of the molecule together like we did with ethane above and show the MOs. At this point we are certainly aware of the fact that four electrons can’t occupy the vector between the two C atoms. This direction is defined by two orbitals pointed in opposite directions to make a σ and a σ* orbital as in Figure A. ■ Pauli’s Exclusion Principle tells us that if we put four electrons in this direction, two of these electrons have to go in σ* because one electron owns a specific set of quantum numbers that no other electron can have. Mother Nature avoids putting the extra electrons in the high energy σ* by using an orthogonal directional orbital for bonding. The only orbital orthogonal to the spn hybrid (where n = 1 or 2 or 3) is p. Hence this second bond must be constructed from p orbitals.

If you got lost in that explanation, let’s clear things up by using the concept of AO hybridization to build the MO energy diagram of H2C=CH2 in a manner analogous to the way we put H3CCH3 together. For this we need half of the H2C=CH2 structure, H2C, namely methylene. In the preceding chapter we got to the electronic structure of methyl anion by removing H+ from methane. When we did so, the MOs did not change that much because the same number of electrons stayed on the C atom. In a similar manner we can take H+ off methyl cation without perturbing the electronic structure so much. Again, the electron count at the C atom remains the same. CH3+ has 6 electrons around the C atom and so does neutral CH2.

Remember that methyl cation adopted a flat structure due to the energetic advantage of putting electrons in orbitals with s character. Mother Nature empties a p orbital to put the six valence electrons in three sp² hybridized ψ_CH MOs. Leaving a pure p orbital empty makes the most sense because these are relatively high-energy places for electrons. Since all directionality is acquired from p orbitals the rehybridization of CH₃⁺ confines the CH bonds to 2D with the inability to explore the 3^rd dimension. Similar rules apply to methylene.

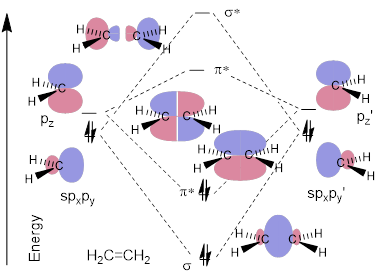
Figure D. A simple MO energy diagram of ethylene from two methylene fragments.

In the figure above, we ignore the rest of the σ_CH framework and focus on the parts of the CH₂ MO that must change the most in the construction of H₂C=CH₂. On the left and on the right in Figure D, there is an s(px)(py) hybrid – an sp² hybrid MO – directed along the vector of bond formation. Also, a pz orbital is orthogonal to the direction of bond formation. Because the sp² hybrid MO and the p orbital are orthogonal, they don’t interact with each other when the molecule is assembled. A σ bond forms in head-on overlap between the two sp² hybrid AOs and a π bond forms in parallel overlap between the two p carbon AOs. These bonds, of course, have antibonding partners in σ* and π* respectively.

We have two ways to make covalent bonds: 1) head-on (σ) and 2) parallel (π). Initially one might expect that the occupied sp² orbitals will remain occupied when they make the molecule. That would put the electrons in σ* in the MO energy diagram, but electrons don’t work that way. That is not the way you built the periodic table in General Chemistry. Electrons occupy the energy levels sequentially, so they will fall to the π level as shown in the middle of the figure.

Orbitals interact head-on to a greater extent than they interact in a parallel fashion, and this fact puts the σ bond at lower energy than the π bond in the MO energy diagram of H₂C=CH₂. The same effect moderates the destabilization of the σ* compared to π* in energy. This one concept applies broadly across organic structure and reactivity, so we will cite it many times.

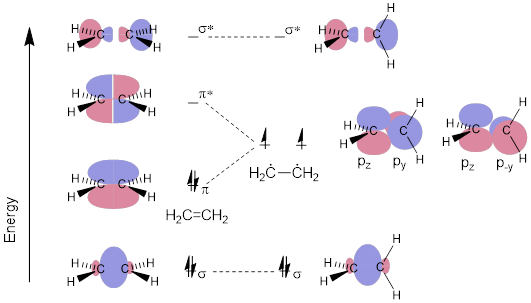
Figure E. MO diagram for bond rotation of CH₂=CH₂ with concomitant π bond breakage.

Another feature of the simplified MO energy diagram of ethylene is the HCCH dihedral angle, which is held at 0°. If the dihedral angles change – for example, if the HCH atomic array on one side of the molecule where 90° apart from the HCH moiety on the other side of the molecule – the MOs of the π / π* pair would become p AO_Cs disposed at 90°. See the MO diagram above; note what happens to the electrons in the π bond. In other words, we can break the π bond in H₂C=CH₂ without breaking the σ bond. Remember that the σ bond is rotatable. Obviously due to the dependence on the directionality of the parallel interaction of p orbitals the π bond cannot rotate and survive like the σ bond does. Isn’t it curious that this fact is not evident from the line structure and that we need MOs and their directionality for the π bond to make sense?

Above we cited the rotational barrier for ethane (H₃C−CH₃) to be 12.1 kJ /mol, which led to rotation about the single bond at ~30 billion times a sec at ~25 °C. The rotational barrier of ethylene is ~272 kJ /mol, which translates to one rotation in 10,000 billion, billion, billion years at ~25 °C.

3.2.1 Molecules with π Bonds Related to Ethylene (Ethene)

We don’t think about the chemical events that lead to bond rotations in ethane and longer chain hydrocarbons as producing separate molecules. These conformational changes or changes in molecular shape happen many times per second in a collection of molecules. They are all dancing and at any point; if we take a picture, every one of them almost appears to be in a different posture. We just learned from the MO picture of H₂C=CH₂ that the C−C=C−C dihedral angles in alkenes are quite a different matter because their double bond dihedral angles are frozen in place.

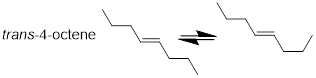
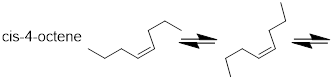
Figure F. Single bonds rotate and change the shape of the molecules with time.

Trans-4-octene is a different molecule than cis-4-octene. When these two molecules are combined, they are difficult to separate. Bulk distillation – even with a technical apparatus – is not successful due to nearly identical boiling points at ~122 °C. However, the more discriminatory technique, ■ gas chromatography, can separate this mixture.

3.2.2 Naming Alkenes

Note: Be able to name the alkenes with C-atom chains from 1 - 10. Look at the names of the alkanes above. We don’t have to worry about methane ever having a double bond, but for the rest changing the ending suffix ‘ane’ and replacing it with ‘ene’ will give you the name of the molecule with the double bond.

We need to discuss a few additional features when naming alkenes. See trans-3-hexene and cis-3-hexene below. The number indicates where the C atom that has a π bond is found in the chain, here carbon 3. Cis- or trans are used if there are two identical groups on either side of the double bond; trans indicates that functional groups are on opposing sides of the carbon chain while cis indicates that the two groups are on the same side of the carbon chain.

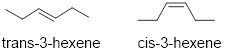
What terminology should we use when the groups are either side of the double bond are different? We should assign these groups as either (E) or (Z). (Z) comes from the German word zusammen, which means “together” and (E) comes from the German word entgegen, which means “opposite”. When examining each carbon of the double bond, we determine the highest priority group (based on atomic number). On one side is an ethyl group and on the other side is a fluorine atom (we will discuss naming halogens later in the class, but for now we are just using fluorine for the example below). If the two highest priority groups are on the same side, we call the molecule (Z), and if they are on opposite sides, we call the molecule (E).

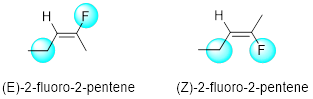
Hopefully it makes sense that E and Z and cis- and trans- are not needed with ethyene or 1-octene (or octene, as the 1 is implied for terminal alkenes) for that matter, as neither have ■ geometric isomers.

3.3 PARALLEL MO INTERACTIONS IN GENERAL

(Arthur Cammers, 2019)

As the MO energy diagram for ethyene by way of two methylene fragments indicated above, when two fully occupied AOs or MOs interact, the net energy of the four electrons increases. In the case of forcing the two lone pairs together for the methylene (Figure D), the electrons are raised in energy to π bonding MOs. If these low-energy π orbitals were not available, the filled/ filled orbital interaction would have led to instability as in the example below wherein two methyl anions are being hypothetically pushed toward each other.

As they get closer, the antibonding component of the interaction worsens. The concepts that we have learned in use here are the following.

1) Conservation of orbital number: there are two occupied orbitals interacting, so we need to be looking at how these two orbitals change.

2) When orbitals interact, they make linear combinations of orbitals.

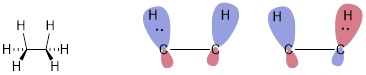
In the case of the two methane orbitals, we change the sign of one to make two irreducible representations of the orbital interaction. The bonding and antibonding components of this hypothetical interaction of methyl anions are shown below. This head-on interaction is strongly repulsive in terms of electrostatics and in terms of Pauli exclusion at the MO level.

The concept that occupied orbitals interact in energetically uncomfortable ways was subtle in the high-energy conformation of ethane when the σ bond rotated to put the three HCCH dihedral angles at 0°, shown below. This interaction is a few orders of magnitude weaker than the interaction of two methyl anions. (Remember that orbitals interact less strongly in a parallel (π) mode than in the head-on (σ) mode.) Across the CC bond, each of the eclipsed CH bonds has three interactions. For clarity, only the in-plane pair of interacting CH bonds is shown below explicitly in terms of interacting MOs (bonding and antibonding, both occupied). Again, these interactions raise the energy of the electrons a little when the molecular shape changes slightly to put these bonds in the same plane. The interactions are repulsive, but they are weak due the electrons are already in bonds.

On the other hand, when occupied and unoccupied MOs interact in a parallel (π) mode, the interaction always stabilizes the energy. Some stabilizing MO interactions are also weak like the parallel stabilizing interaction between occupied σ and unoccupied σ* in ethane in the low-energy position of the HCCH dihedral angles (180°) shown below. In this case the antibonding combination (right) is unoccupied so its energy does not undo the stabilizing energy of the bonding combination (left).

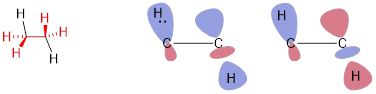
Here we must switch the sign to show the antibonding component of the MO interaction, but unlike the destabilizing interaction above, there are only two electrons to occupy this pair of bonding and antibonding orbitals. The bonding MO interaction is occupied and thus stabilizes the energy of the positions of nuclei that put the σ bonds pointing in opposite directions. This parallel interaction is weak because σ and σ* are so far apart in energy, but in this case the bonding (occupied - unoccupied) orbital interaction is the major energetic part of the barrier to rotation of ethane! The antibonding (occupied / occupied) orbital interaction is the minor energetic part of the barrier to rotation of ethane that contributes to the low barrier of CC σ bond rotation.

Of course, when two parallel orbitals are partially filled, we must represent that interaction as a strong π bond / antibond pair. This is the reason we don’t draw two dots on two pyramidal C atoms below in ethylene. The HCCH improper dihedral angle is 0°; the six atoms in the molecule are coplanar to optimize the parallel interaction of the two p orbitals. Since the π bond is occupied, it contributes to the energy of the electrons in the molecule, but the unoccupied π* orbital does not.

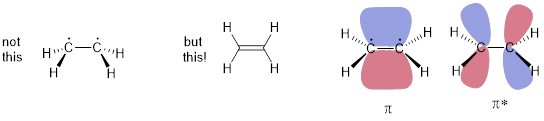
3.3.1 Resonance Structures Involving Double Bonds

Hopefully you can see that we have come full circle from Chapter One. You may recall an earlier description of resonance structures involving multiple line structures to explain delocalized electrons in molecules. We needed to draw at least two structures to explain the real structure. This concept of structure in organic chemistry predates quantum mechanics. Let’s revisit molecules that putatively require more than bond-line structures to explain their geometry and reactivity; perhaps we can update our structural theory. The example that I am referring to is in Chapter One and is shown below.

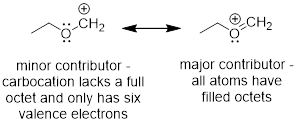
Now we have another way to describe line structures that require multiple resonance structures. I’ll iterate the example of resonance structures with the cation adjacent to an O atom and the π bond below. It is impossible for the electrons to stay on the O and not flow into the AO on C just like it is impossible for a half full cup of coffee to fully occupy the left side of a coffee cup.

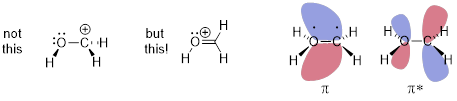
The empty p orbital in the next atom is always a place for electrons to go and if electrons can go there, they are already there. The ability of the O atom to stabilize electrons better than the C atom can be captured in the unequal sizes (coefficients) of the orbital values at O and C. More electron density resides around the O atom than the C atom in this π bond. Whatever the bond does the antibond does the opposite, so larger mathematical coefficients are associated with C atom in the unoccupied orbital shown above. In the coffee cup analogy, this might be a half-filled cup of coffee under constant acceleration.

Again, these strong electron-energy minimizing interactions occur because the two orbitals that interact are not both occupied and the electrons are not in bonds before the orbital interaction is considered. When both orbitals are occupied, the interaction is always destabilizing (antibonding) if the atoms come near bonding distance.

If we are still stuck on resonance structures, we can add yet another rule for their construction: Good resonance structures preserve the hybridization of the bonds at all atoms.

Exercise 3.3.1 Determine how the CH bonds are hybridized at the C atom in two resonance structures used in the example above.

3.4 STRUCTURE OF ACETYLENE

(Arthur Cammers, 2019)

H−C≡C−H, properly referred to as ethyne, but commonly called acetylene, is a linear molecule, but then again you knew that at a glance. At this point you are hopefully parsing line structures into molecular geometries quickly. You know that there can only be one σ bond between two atoms, and since there three lines are drawn between the C atoms, there must be two π bonds. At each atom there must be two orthogonal p orbitals to engage in π bonding. The σ CH and σ CC at each C atom must therefore be sp hybridized. Since these σ bonds only have one directional orbital component, they must be confined to a line and therefore can’t explore the 2^nd or 3^rd dimensions. For the sake of completeness and to give you a little more practice in building orbitals, let’s set up the directional hybrids in terms of MOs.

3.4.1 MOs of Acetylene

To build the MOs of acetylene, we must hybridize s and px, and will leave py and pz as pure (unhybridized) p orbitals. The directional vectors are [1] and [−1], if you want, [1, 0, 0] and [−1, 0, 0]. In any case, the bonding cannot explore the y and z directions since these are used in the formation of π bonds. We can easily confirm that the bonding array uses the p orbital equally with this bonding scheme by summing the two vectors. [1, 0, 0] + [−1, 0, 0] = [0, 0, 0].

To build an MO picture, let’s make the hybrid MOs at one C atom. The hybrid MOs are one part s and one part p. AO_C1 = √½s + √½px and AO_C2 = √½s − √½px. We can envisage this mixing as the simple imposition of plus and minus px onto the s orbital in Figure G and we can make CH σ bonds for the CH fragment in Figure H. Figure I combines two CH into C₂H₂, or HCCH.

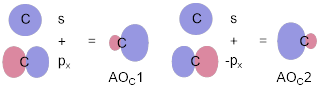
Figure G. The two spx hybridized AOs at C. The p_z and p_y orbitals are not shown.

Figure H. An MO picture of the neutral HC fragment, methine.

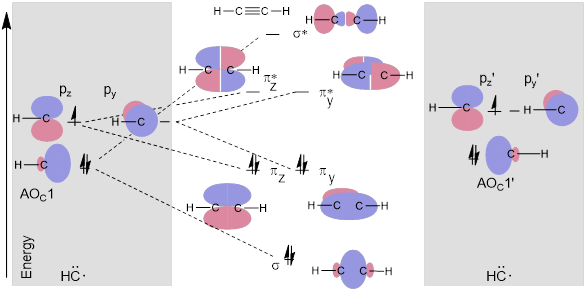
Figure I. A simple MO energy diagram of acetylene from two methine fragments.

In Figure I, pz on the left methine reactive fragment does not interact with py’ on the right-side methine reactive fragment. The py and pz’ AO_Cs are orthogonal (90° away from each other). However, the two pz orbitals combine to make the π_z and π_z* MOs. Likewise, two py orbitals make π_y and π_y*. The py and pz orbitals are orthogonal to the spx hybrid so they don’t interact when the σ bond forms. Thus, in the MO diagram above, pz, py, and AO_C1 of methine are split into three orthogonal bonding and antibonding components of H−C≡C−H by their symmetry-matched partner orbitals − pzʹ, pyʹ and AO_C1ʹ − to make bonds, their electrons decrease in energy.

3.4.2 Molecules with π Bonds Related to Acetylene

In terms of hydrocarbons, we covered alkanes and the alkenes and now only the alkynes remain. As you might imagine, analogous to the way we name these chains, naming the alkynes just snips off the ‘ane’ from the name of the alkane and adds ‘yne’. Thus, the six-carbon atom chain consisting only of C and H atoms but possessing a triple bond is referred to as hexyne instead of hexane. Furthermore, like the alkene needs a number to denote the position of the double bond, the alkyne needs a number to denote the position of the triple bond. There is 1-hexyne (or hexyne), 2-hexyne and 3-hexyne; however, monikers like cis-, (Z), trans-, and (E) are not necessary. Alkenes can dispose the C atoms on the same side of the double bond or on the opposite side of the double bond. Since the double bond does not rotate, we need these designations for alkenes. We do not need them for alkanes because they freely rotate; we do not need them for alkynes because they are linear.

Note: When you use line structures to draw alkynes draw them straight.

Note: When you use line structures to draw alkenes draw them bent. If you draw them straight the person with whom you are communicating will not know if you are talking about the E or Z isomer.

3.5 CHEMISTRY AND PI BONDS

(Arthur Cammers, 2019)

Certainly, there are more molecules with more saturated (sp³) atoms than unsaturated atoms (sp² or sp); however, look again at the MO energy diagrams and realize that decreasing the potential energy of electrons in molecules is Mother Nature’s usual game. She is therefore less interested in changing the nature of the low-energy electrons in molecules; they don’t bug her so much. When conditions allow changes in molecules to happen, she tries to make a change to bring the highest energy electrons down in energy. Isn’t this basically the definition of chemical bonding?

With the above notion in mind, go back and put new significance on the nature of the bonds and their energies in the MO energy diagrams above. You will almost always see that π bonds are higher in energy than σ bonds. Furthermore, it is worth noting that electron lone pairs on atoms tend to be at higher energy (more reactive) than their π bonds. The constitution of these lone pairs are basically atomic since they are not part of a bond, and the definition of a bond is the interaction of two orbitals and the decrease in energy of the corresponding (1 is possible, but most often 2) electrons.

This means that some organic chemistry is molecular change driven by the instability of lone pairs and π bonds. Most of the complicated reactions that we study involve π bonds in double and triple bonds. Again, this is due to the relative efficiency of σ bonding compared to the less energetic π bonding. Interactions of parallel AOs and MOs have the potential to decrease the energy of electrons in molecules less than analogous interactions of AOs and MOs directed at each other.

It makes sense to draw the MO energy diagrams like the examples above, with much of the σ bonding implicit in line structure format and with the π-derived MOs explicit in colored objects. It is also reasonable to be concerned with shape and directionality and how well the AOs interact, given that the π bonds and lone pairs determine most of the chemistry.

Exercise 3.5.1 (a) Draw 2-heptyne. (b) How many isomeric straight-chain heptynes exist? In a straight chain, each C atom may be connected to a maximum of 2 C atoms.

Exercise 3.5.2 (a) Draw decyne. (b) How many isomeric straight-chain heptynes exist? In a straight chain, each C atom may be connected to a maximum of 2 C atoms.

Exercise 3.5.3 Think about the following: B:⁻ + H⁺ → BH represents a base reacting with a proton. This is the proton transfer reaction you discussed in General Chemistry. If the electrons on B are higher in energy, B is more basic, and the equilibrium of the reaction favors the right side. (a) Of the molecules A, B, and C below, which is the most basic (most reactive with H⁺)? Which one is next most basic? (b) Provide an explanation for the difference in basicity. (c) Draw bond-line structures of the conjugate acids of A – C.

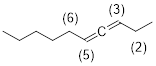
Exercise 3.5.4 Consider the hybridization in the 3,4-decadiene below. What is the value of the C2-C3-C5-C6 dihedral angle?

3.6 THE PI ALLYLIC ORBITAL SYSTEM

(Arthur Cammers, 2019)

Let’s explore these parallel interactions in greater detail and unveil their importance to the structure and reactivity of organic molecules. The electron-energy minimizing effects that result when multiple p orbitals interact is referred to as conjugation. This effect is a ubiquitous theme in organic chemistry.

3.6.1 The Allyl Cation

In chapter one the allyl cation is given as an example in which we need two resonance structures to describe the real structure, a resonance hybrid. But with our understanding of the way AOs and MOs interact this picture seems overly complex. The allyl fragment simply has an sp²-hybridized σ bonding framework that must be in the same plane (e.g. xy plane) in the lowest energy position of the atoms. Additionally, a π system made of 3 pz orbitals must all interact to stabilize two electrons.

Expecting that the electrons in this π system stay on the right side of the molecule or stay on the left side of the molecule is … well the half-filled cup of coffee again. Let’s see how these parallel AOs interact to form MOs. First, we know that we are looking for three MOs that are irreducible representations of the three-part interaction. Remember that irreducible means when we multiply by −1, we do not convert any one of them into another. We already have the MOs of ethylene, namely π and π*. Let’s start there and interact these orbitals with another p orbital according to the way orbitals interact.

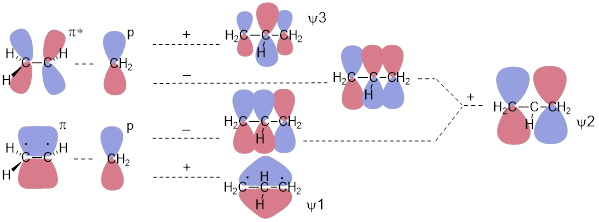
Here we will ignore the σ framework. To make things work, we need to replace an H atom with a CH₂ unit. The focus here is how the pz orbitals interact to make the three-component π system of MOs. Addition of the p orbital to the π bond gives us an orbital with zero nodes, an all-bonding ψ1. Because ψ1 lacks nodes, we recognize it as the lowest-energy MO in the system. Likewise, addition of the p orbital to π* gives us an MO with two nodes – two antibonding interactions between atoms. We immediately recognize this as the highest-energy MO in the three-component π system (ψ3). We reach a bit of a complication when we subtract the p orbital from (add the negative p orbital to) π and π*. This gives us an asymmetric result with one node. There is a bonding interaction (no sign-change going from one C atom to the next) and an antibonding interaction (the sign changes going from one C atom to the next) in both MOs. When we add them, we get an irreducible representation, meaning that it can’t be converted into ψ1 or ψ3 by multiplying by −1. This addition installs one symmetric node at the central C atom. We call the orbital that results ψ2. The addition of two dissymmetric MOs is nothing new; we did this to make the offending orbital space on the H atom disappear in the σ system of methyl cation in the last chapter.

There are only two electrons in the π system of allyl cation meaning ψ1 is occupied and that ψ2 and ψ3 are empty.

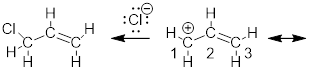
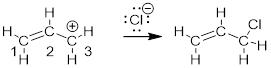
The resonance structures for the allyl cation supposedly allows us to explain why C atoms 1 and 3 react with a species capable of donating electrons to make a bond. But since we know: (1) empty and occupied orbitals interact to make bonds; (2) we have a picture of the lowest-energy unoccupied orbital (LUMO); ψ2 and (3) orbital lobes determine where electrons can go. We know that the LUMO, ψ2, will receive the electrons in the final C-Cl bond and it is allowed space only on C atoms 1 and 3. There is a node at C2 − a place where electrons cannot occupy. The reason the electrons on Cl⁻ do not interact with ψ1 in the reaction shown above is because ψ1 is fully occupied. The reason the electrons on Cl⁻ do not interact with ψ3 is because unoccupied ψ2 is lower in energy than unoccupied ψ3. When a molecule behaves like a Lewis acid in that it accepts electrons, its chemistry is determined by the LUMO.

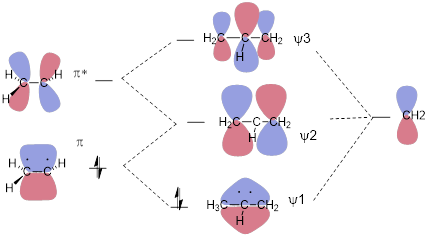
Figure J. A simple MO energy diagram of the allyl cation.

In the figure above, we slid an empty p orbital within bonding distance of a π bond and generated the allyl MOs. In the all-antibonding ψ3 orbital, the central coefficient of the wave function increases to balance the opposite effect of the bonding interactions. In the all-bonding ψ1 orbital, the central coefficient of the wave function increases to optimize the bonding interactions on either side of the middle C atom. There is math that allows us to compute the enhancements of these p orbitals. A person can do this math on the back of an envelope with a pen, and by that, I mean without the aid of a computer. I’d love to show it to you, but that would require at least half of the semester. If you continue to study chemistry, you’ll see this at some point in an advanced class.

3.6.2 The Allyl Anion

Fortunately reworking the allyl system to explain the allyl anion in terms of structure and reactivity is not necessary since we have already done this for the allyl cation. In this case, occupying the cation versus the anion is just a matter of filling the relevant orbitals, which we can do by counting electrons. The anion simply has two more electrons than the cation. Those two extra electrons of the anion occupy ψ2. However, for the allyl anion, ψ2 is now the highest-energy occupied MO (HOMO). Since the anion has high-energy electrons, it will function as an electron donor − a Lewis base − to make bonds: The allyl anion will seek an unoccupied orbital in another molecule with which to bond. In a base, the chemistry is determined by its HOMO just like the chemistry of the Lewis acid (cation) was determined by its LUMO. Again, the reactivity of the base is at the terminus because ψ2 tells us that the electrons are there, with no electron density at the middle C atom.

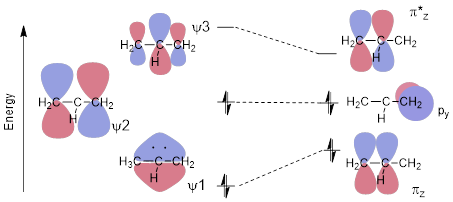
Figure K. MO energy diagram of the allyl anion (left) twisting out of planarity (right).

Another interesting aspect of the anion establishes a phenomenological relationship to the π bond in ethylene. All atoms are coplanar in the lowest energy geometry of both the allyl cation and anion. With ethylene, if the bond rotates, the p orbitals are no longer parallel and cannot engage in π bonding. If one of the σ bonds in allyl cation or anion rotate, it is ψ1 that is perturbed the most because that is the MO that loses bonding interaction (see Figure K). When the p orbital C atom is 90° to the π bond, the system is modelled best by a π MO, a π* MO, and an orthogonal atomic p orbital as in the right side of Figure K. In any case, the energy of the molecule increases, so Mother Nature likes to leave the allyl molecule − whether cation, anion or radical − in flat conformation.

When twisted, the energy of the allyl system does not change as much as compared to the energy required to twist the two ends of ethylene out of planarity. There are ways to calculate how much energy is lost upon twisting of one molecule versus the other, but there again you will have to wait for an advanced chemistry course. We are only laying the groundwork here for qualitative organic structure that we can reach with minimal mathematics and cartoons of MOs.

3.6.3 The Allyl Radical

There really is not much to say about the allyl radical. We have a lot to develop about the details of the chemistry of the radical, cation, and anion, but in terms of structure and the attendant MOs, not only is this just another question of occupancy, but that occupancy is intermediate between the cation and the anion.

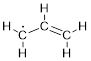
In the case of the radical, ψ2 is partially occupied. For radicals, the half-occupied MO is often referred to as the SOMO, or the singly occupied MO, although it is technically the HOMO because Here again ψ2 determines the chemistry of the radical species. The orbital coefficients at C atom 1 and 3 tell you where the electron can go and where the single electron is. The again the node at C atom 2 tells you that any reactive species that putting an electron at C atom 2 or getting an electron from C atom 2 will not result in bonding.

3.6.4 Allylic MOs in Many Organic Molecules

We have not wasted any time in the development of the MOs for the allylic system because many organic molecules and organic functional groups have 3 interacting p orbitals that form allylic systems and can therefore be understood by considering the allyl π system. From the general description of the allylic system, small corrections get us to an understanding of their properties. For example, let’s have a look at an amide − in this case formamide − at right, compared to the allyl anion at left, below.

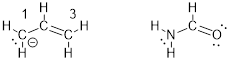
We can certainly draw resonance structures for these two molecules. In the case of the allyl anion, switching the position of the π bond generates the resonance structure below. In formamide the analogous resonance structure puts the double bond between N and C instead of O and C. Also, for this resonance structure, the N atom gets a formal positive charge and the O atom a negative charge. These resonance structures are shown below.

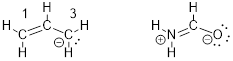
We understand from the analogy to the allyl anion that rotation of the amide NC bond is at least partially restricted. We also expect that the nitrogen atom is flat with H-H-N-C improper dihedral angle = 0°. We might have predicted the H-H-N-C improper dihedral angle to indicate a pyramidal configuration, but in light of the MOs, we parse the structure into something quite different.

The π MOs also indicate Lewis base-like reactivity at N and O for the amide. Given a chemical context, having either atom function as an electron donor (Lewis base) would not surprise us. All these statements are true for the amides, and all from very simple quick realization that three contiguous orbitals with the number of electrons of the amide and positioned parallel should be essentially an allyl anion system.

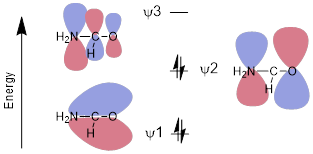
The MOs of the amide should be polarized toward the most electronegative atom (O) in the bonding, and the non-bonding MOs should be polarized toward the relatively electropositive atom (N) in the antibonding MOs.

Many molecules that we will consider this semester have allylic orbitals. A few are drawn below.

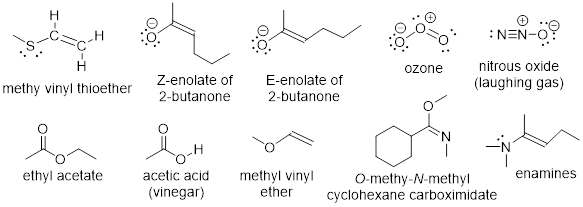
Exercise 3.6.1 Laughing gas has a triple bond and no double bond. Why can we include laughing gas in the list above?

Exercise 3.6.2 How should ψ2 in ozone and ψ2 in allyl anion differ? Give this a few minutes of thought. This may require some insight. Use the answer as a learning opportunity.

Exercise 3.6.3 Does the effect of electronegativity kill electron donor reactivity at the C atom in the enolate of 2-butanone (shown above), or should we expect to see the C atom also acting as a Lewis base?

3.7 BUTADIENE AND CONJUGATED PI BONDS

(Arthur Cammers, 2019)

The last fundamental aspect of electronic structure that we must understand before we can generalize electronic structure in any organic molecule is conjugation, a phenomenon in which p orbitals interact to minimize electron energy through delocalization. We looked at two p orbitals interacting to make a π bond and three p orbitals in the allylic system. The effect of conjugation of p orbitals in unsaturated carbon atom chains continues in 1,3−butadiene, H₂C=CH−CH=CH₂. Given the theory that we have so far, I might ask you if you expect some hindered rotation in the C2-C3 bond of H₂C=CH−CH=CH₂. This thought might make you pause, but at least at this point you know the recipe to answering the question: Step 1) Get an idea of what the MOs are like in 1,3−butadiene. Step 2) twist at the C2-C3 bond and determine if the MO energy diagram changes. If the total energies of the occupied orbitals increase, then the C2-C3 bond should have some hindered rotation and all four C atoms should be at lowest energy when coplanar.

Step 1: We can get the MOs of 1,3−butadiene by interacting the π systems of ethylene. If we bring the ends of ethylene together and focus on the parallel interactions, we should be able to construct at least crudely how the MOs of 1,3−butadiene dispose themselves in energy. We built ethylene by adding and subtracting the p orbitals at C to get π and π*. A similar approach gets the MOs of 1,3−butadiene straight away.

Ψ1 = π + π, Ψ2 = π − π, Ψ3 = π* + π*, Ψ4 = π* − π* and that is all the π MOs we need because there are four atomic p orbitals at each of the four C atoms in 1,3−butadiene.

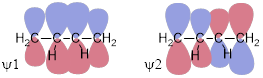
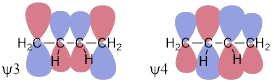
This approach generates the MOs above. We can see immediately that ψ4 is of highest energy with 3 nodes, ψ3 is next highest in energy with two nodes, ψ2 − with one node − should be the HOMO because there are four electrons in the π system of 1,3−butadiene. ψ1 should be the lowest-energy (occupied) MO because it has zero nodes. But I should know this, because that is how I named them from lowest to highest energy based on the number of nodes in each. How do we know that there are four electrons in the π system of butadiene? How do we know that there are two electrons in the π system of ethylene? We count the electrons that should occupy p orbitals in the structure. In 1,3−butadiene, H₂C=CH−CH=CH₂, we see that there is a bond in excess of a single bond between C1 and C2 and between C3 and C4. We know that these must be π bonds because there can be only one σ bond between two atoms due to the Pauli Exclusion Principle. Those lines mean two electrons in a π bond and since there are two lines there are four π electrons.

At this point, we know that rotating the C2-C3 bond will make the two halves of the molecule behave like separate ethylene π systems (see the MO diagram above) and will no longer interact because they are not parallel. There should be a slight preference for the flat structure because occupied ψ1 increases in energy due to loss of the bonding interaction between C2-C3 in ψ1.

If 1,3-butadiene were to form a bond by donating a pair of electrons to a Lewis acid, at which C atom would the Lewis acid react? The quick answer has us looking at the orbital coefficients of the HOMO, ψ2. These are largest at C1 and C4. Let’s take the logic a little slower to make more sense out of it.

We can expect that the orbital coefficients of C2 and C3 should be big in ψ1 because these are between two bonding interactions whereas the coefficients at C1 and C4 in ψ1 should be smaller because these are affected by only one bonding interaction. Mother Nature enhances the coefficients to optimize bonding and to minimize antibonding in bonding orbitals. Realizing this allows you to rationalize the relative sizes of each of the coefficients in ψ1 and ψ2. Realizing that MOs optimizing bonding in this way gives us a rational of how conjugation stabilizes electrons in orbitals. The bonding of conjugated orbitals decreases electron energy due to greater interaction between orbitals of the same phase. Conjugation makes a similar statement about the antibonding orbitals, but toward destabilization. The antibonding orbitals in conjugated π systems increase in energy due to greater interaction between orbital coefficients of different phase, thus in ψ4, the C2 and C4 coefficients are largest due to the two antibonding interactions. Of course, the bonding orbitals are the occupied orbitals, and this effect stabilizes the molecule, and of course, the antibonding orbitals are the unoccupied orbitals, and this effect has no effect on the molecule.

We know that the electron pair will come from ψ2 because ψ2 is the HOMO. The only other place the electron pair could come from is ψ1 or from one of the σ_CC or σ_CH bonds. These options are all lower in energy than the electrons in ψ2. The coefficients in ψ2 are largest at C1 and C4 due to the bond enhancement and antibond abatement of the coefficients so that is where the electrons are, mostly, on average. Since that is where the electrons are in the HOMO, that is where butadiene reacts with Lewis acids − at C1 and C4.

Exercise 3.7.1 In 1,3−butadiene, and the ‘buta’ portion – like ‘butyl’ – should indicate to you that four C atoms are contained in a linear chain, and the ‘diene’ portion tells you there are two alkenes in the molecule, resulting in all atoms being unsaturated. Think about the obvious naming convention. (a) Can you draw the line structure of 2,4-hexadiene? (b) Can you draw the line structure of 1,8-nonadiene?

3.7.1 Shortcut to Building Conjugated π MOs

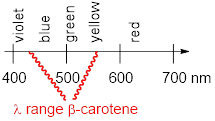
We looked at p orbital systems of one C atom in methyl cation and radical, and we have gone to p orbital systems four C atoms long in butadiene. However, there are many molecules with long conjugated π systems that we need to understand with very little ceremony. For example, ■ ß-carotene relies on 11 conjugated π bonds for its molecular properties; it sits in a protein called ■ rhodopsin in the retinas of our eyes and allows us to see. To manage ideas involving molecules like carotene, we need to have greater facility with the MOs of conjugated π systems. Let’s look into a shortcut to building long MOs quickly.

Looking down on the π system from above, the first MO has no nodes. Increase the two central coefficients relative to the terminal coefficients to optimize bonding. This optimizes bonding because the orbital coefficient at C2 has two bonding interactions with that of C3 and C1. However, the orbital coefficient at C1 has only one bonding interaction with C2. If the orbital coefficient at C2 increases, the bonding interaction must increase.

The second MO has one centrosymmetric node. Downsize the two inner coefficients a little to minimize the antibonding interaction and enlarge the termini coefficients to optimize bonding interactions.

The third MO has two centrosymmetric nodes. Increase the two inner coefficients a little to increase the antibonding interaction in this net antibonding orbital. What the bond does the antibond undoes.

The fourth MO has three nodes that coincide with previous nodes in ψ2 and ψ3. The coefficients look like those of ψ1.

Exercise 3.7.2 Given that nodes can occur at atoms − not only at bonds between atoms − repeat this method for the construction of the allyl π system. Check your results with the allyl π system worked out above.

Exercise 3.7.3 You should be getting pretty good at this. Repeat the process for the pentadienyl radical: •CH₂−CH=CH−CH=CH₂. How many electrons are there in this π system? Which orbital is the highest-energy occupied orbital? Is this orbital a HOMO or a SOMO?

Check your work by Googling the words: ‘pentadienyl MOs image’. See people’s MOs, and look at a few to make sure the ones you are looking at agree with each other. Look at the different ways these are presented. Some people may worry about the sizes of the MO coefficients and others can’t be bothered.

Exercise 3.7.4 This deep look at MO theory has given us the ability to touch a subject quite far into the future in terms of the usual order of subjects people study in organic chemistry at this stage. Think about benzene and guess at the MOs. The line structure does not give us a clue regarding about the exceptionally stability of the electrons in the π system. The effect is called aromaticity. The benzene ring is an aromatic structure.

(a) Draw the MOs of benzene. To do this, look down on the structure from above as I did in the abbreviated rules for drawing extended MOs. (a) How may MOs are you looking for? (c) How may electrons are part of the π system? (d) Arrange the MOs in energy in an MO energy diagram.

Hint: Follow the rules above. However, there are two ways to make ψ2. This generates 2 MOs ψ2 and ψ3 of the same energy. There are also two ways to make ψ4 and ψ5.

Hint: To arrange the MOs in energy count the bonding and antibonding interactions in the MOs.

Check your work by Googling ‘MO energy diagram benzene’, and click on image for a lot of different images of the MOs of benzene. How well did you do?

3.8 LOCAL NATURE OF Sigma AND THE GLOBAL NATURE OF Pi

(Arthur Cammers, 2019)

Even though we did not discuss many specific cases here, hopefully you are putting the pieces together to make a recipe for chemical changes in molecules and molecular structures. Occupied orbitals react with unoccupied orbitals to make bonds. Occupied orbitals interact favorably with unoccupied orbitals to help determine the shapes molecules prefer. Occupied orbitals interact unfavorably with occupied orbitals to determine molecular shape. The strength or importance of these interactions is complicated but intellectually tractable by considering low level concepts, putting together the little bits and pieces.

The notion that σ bonds affect structure and reactivity locally while π bonds can affect molecular structure and reactivity at larger length scales characterizes a major difference between σ and π bonding. We will see that conjugated π systems can make σ bonds easier to break and can also stabilize otherwise high-energy chemical intermediates. For example, the CH bond below requires less energy to break in 1,3-pentadiene than it does in methane. Because of conjugation, the energy of the pentadientyl radical intermediate is much lower than the energy of methyl radical.

We will study some reactions that do not happen at all without the assistance of conjugation. Look again at ß-carotene; all the electrons in π bonds from one end to the other are talking to each other and thereby enabling the molecule to synergize with the protein rhodopsin to let us detect light.

3.8.1 Saturation Truncates Conjugated Systems

Infinitely unsaturated systems can have long MOs and have very stable electrons in π bonds, but the effect stops at points of saturation. For example, the maximum length of the π MO in 1,4−pentadiene, H₂C=CH−CH₂−CH=CH₂, is two C atoms long. Here a pair of ethylene MOs is a good first approximation to describe the π system. The point of saturation (−CH₂−) in the middle of the molecule basically truncates the electronic communication in the π systems on either side of the methylene unit. To have the neat effects of MOs with multiple nodes, the valence needs to be ‘open’ at all atoms. The bonded electrons in σ_CH of the methylene units interact only weakly with the π MOs that flank it. We can open the valence site at the central C atom as in the following structures.

We are working with the pentadienyl π system because the non-bonded electrons, half-filled orbital, or empty orbital will interact strongly with the π system. In this case, the lone pair at left is in a pure p orbital and all the σ_CH and σ_CC bonds in this species contain sp²-hybridized C atoms.

Note: The presence of the π bonds on either side of the methylene unit in H₂C=CH−CH₂−CH=CH₂ facilitates any chemistry that allows the generation of the anion, radical, or cation. In this way, π systems impact reactivity at saturated atoms even though the saturation truncates the size of the MO.

3.9 BOND AND ORBITAL HYBRIDIZATION UPON INSPECTION

(Arthur Cammers, 2019)

Since much of chemical reactivity and most organic molecular geometries can be had from being able to state the bond and or orbital hybridization at any particular atom in a molecule, we need an abbreviated means to this end. The crux of the task is counting the p orbitals at the atom of interest and then assuming the molecule mixes the remaining s and p orbitals to construct the σ bonding array and to contain any remaining lone pairs. Let’s take a few examples so you can understand how to use the background established above to quickly discern orbital mixing and molecular geometry.

Example 3.8.1

How is the C─H σ bond hybridized at the C atom in the vinyl cation?

Solution: To determine hybridization or geometry we simply count pure (unhybridized) p orbitals at the atom in question. There is one pure p orbital for the π bond and another for the unoccupied orbital. Remember that Mother Nature prefers to make this p instead of wasting s character on an empty orbital. Take these two p orbitals out of the running leaves one p orbital and one s orbital to make the CH and the CC σ bonds at the C with the positive charge. One p and s hybridize to sp and the lowest-energy geometry for the HCC bond angles is linear.

Exercise 3.9.1 How are the atoms in the CH bonds in ethylene (H₂C=CH₂) hybridized?

Exercise 3.9.2 How are the atoms in the CH bonds in acetylene (HC≡C) hybridized?

Exercise 3.9.3 In what type of orbital is the lone pair in acetonitrile (H₃C−C≡N) housed?

Exercise 3.9.4 (a) Which type of NH bond is shorter, the N1−H, or one of the N4-H bonds? (b) Explain your answer.

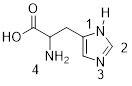
Method: determine which bond has more s character. That is the shorter bond. Count the p orbitals at N1. There is one p orbital at N1, it contains the lone pair at N1 because these electrons are engaged in π bonding with the π system in the ring. If a lone pair is adjacent to a π bond or p orbital it is going to adopt pure p character to enable conjugation to decrease the energy of the electrons. The s and two other p orbitals are used to make the σ framework. N1−H is sp²-hybridized at the N atom.

Exercise 3.9.5 (a) Add the implied electron lone pairs to histidine. (b) Which electron lone pair is the most basic? (c) Explain your answer.

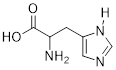
Another way to frame the question might be: Add one proton to histidine and draw a line structure of the conjugate acid. The most basic atom will acquire the proton.

Exercise 3.9.6 Explain how the atomic orbitals are mixed at the N atoms in A and B.

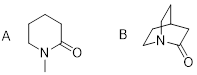
Exercise 3.9.7 In certain reactions involving single electron transfer, chemical species like the one below are visited. These are somewhat embarrassing to draw out as Lewis structures.

a) In which MO is the added electron?

b) Why are these difficult to put in terms of line structures?

3.10 Induction, Polar Covalent Bonds, and Electronegativity

(Arthur Cammers, 2019)

Given your introduction to ■ electronegativity in General Chemistry, you probably think that it is a solid parameter devoid of opinion … something perhaps that one can measure unequivocally. Perhaps you can adjust your view after spending some time with the cited Wikipedia page. You will see that there are multiple electronegativity scales and that some of them have units while others do not. The concept of an atom’s ability to separate charge in a bond is rather murky because there are multiple chemical contexts in which the same bond can be found. Putting an average number on the polarity of a bond is difficult because bond polarity depends on chemical context (what are the elements in the bond connected to? etc.). However, electronegativity explains that the atoms in the periodic table differ in the ability to stabilize electrons, and these differences are manifest in charge separation in molecules.

Regardless, due to the great difference in electronegativity between Na and Cl in table salt, ionic bonds hold the material together, keeping it solid except at very high temperatures and making NaCl highly water-soluble. We’ll unpack the solubility issue in a minute. These atomic ions and their electrostatic interactions result because the neutral sodium atom has a strong electron-donor configuration due to its proximity on the periodic table to neon, which has a full atomic shell as a neutral noble gas. Na• readily gives up an electron to become Na⁺ and thereby adopt the Ne electronic configuration. Chlorine, on the other hand, tends to do quite the opposite and prefers to acquire an electron to become Cl⁻ and thereby adopt the electronic configuration of Ar, the closest noble gas electronic configuration to the Cl atom.

Atomic charged monopoles held together by coulombic attraction is the recipe for the ionic bond; one atom has stolen an electron from the other. On the other hand, a perfectly covalent bond requires equal sharing of electrons between the two atoms joined by the electrons. We can find perfect covalent bonds in diatomic molecules like O₂, Cl₂, and N₂, but when we have a combination of atoms of moderately different electronegativity in a molecule, the bonding is a mix between ionic and covalent, with the result favoring the covalent motif; these bonds are referred to as polar covalent bonds. Polar bonds result when electron sharing is unequal. The CH connections we have been discussing to this point are quite covalent and non-polar due to the similar electronegativities of the C an H atoms.

Consider the fact that the C−O double bond can make a molecule polar (■ acetone structure bottom left). We indicate the molecular polarity with the arrow showing the direction in which we will find most of the negative charge, in this case the dipole vector and the CO bond axis coincide. Bond polarity can also be indicated with −δ and +δ at the atoms at the extremes of the charge separation. People also use charge-separated resonance structures to indicate bond polarity, given that populating the more electronegative element with electrons recovers some of the energy of the broken π bond.

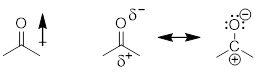
Indeed, there is a continuum of electronic occupation around covalently bound atoms instead of the fully ionic octets. The noble gas electronic configuration from electron population around the O atom is more complete than the octet around the C atom due to electronegativity differences.

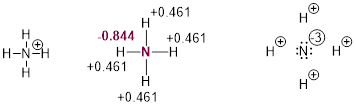
The line structure of ammonium, NH₄⁺, in the upper left has a formal positive charge on the N atom. However, sophisticated computation puts quite a different charge distribution on the cation, with partial charge on the N atom at almost unit negative charge and approximately half a positive on the H atoms. If you accept line structures and the charge notation we use as literal, I urge you to adjust your perspective now to admit the predictive value of electronegativity.

The N atom with the complete octet is closer chemically to the Ne electronic configuration than the H atom with a complete duet is to the He electronic configuration, so N is more electronegative than H and electronegativity mandates partial atomic charge in molecules.

3.10.1 Dipole Moments and Molecular Polarity

Polarity is static charge separation, measured by a vector quantity, , the dipole moment. Dipole moments can describe electron distribution in molecules and in bonds in molecules, although assigning a definite value to a bond is difficult—these are rarely quoted to more than 2 significant figures. Molecules distribute positive and negative charge in space with valence nuclear positive charges and negative charge as electron density in occupied MOs. Quantum mechanical calculations can estimate the positions and intensities of partial positive and negative charges in neutral molecules. If the 3D coordinates of the average positive charge and average negative charge coincide then the molecule is apolar, and has zero molecular dipole moment, as in the examples below.

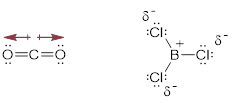
If the coordinates of the opposite charges do not coincide, there will be a magnitude in the charge difference and a direction of the charge displacement relative to the average atomic coordinates of the molecule. In this case, the molecule is polar with a non-zero dipole moment. This moment is a vector, •q in which characterizes the distance and direction between two charges and q is the magnitude of the charge separated. In this calculation, the averaged positively charged centroids and averaged negatively charged centroids will have the same absolute value since the hypothetical molecule is neutral.

3.10.2 The Magnitude of the Debye Unit

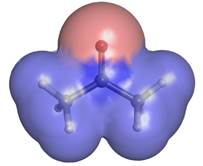■ Acetone, discussed above, has molecular dipole = 2.91 D. The SI unit of the dipole moment is called the debye (D) and can be put in terms of coulomb•m (1 D: = 3.33E−30 C·m). However, since −30 is quite an extreme exponent, changing the units can frame the parameter more comprehensibly. The charge of e− (■ elementary charge) is 1.60E-19 C. The Å is a distance unit relevant to bond lengths. The ■ covalent radii of atoms allows estimations of bond lengths. 1 Å = 1E−10 m, so 1 D: = 0.2082 e·Å; this result is calculated below.

1 D: = 3.33E−30 C·m = 3.33E−30 C·m / 1.6022E−19 (C/e) •1E10 Å/m = ■ 0.2082 e·Å

In other words, if two opposite unit charges (perhaps a proton and an electron) were separated by 1 Å (in the absence of quantum mechanical effects), the resulting electrostatic moment would be 0.2082 e·Å, and it would lie along the vector of separation pointed in the direction of the negative charge. By this standard, the molecular dipole of 2.91 D or 0.606 e·Å for acetone should look remarkable and understandably give birth to measurable ■ bulk properties. Ostensibly, the molecule effects this impressive charge separation by polarizing the O, C and H atoms. Any polarization of the H atom has a greater effect on the dipole moment than the same polarization of the C atom because the H atoms are, on average, farther away from the O atom. Bear in mind that the dipole moment directly depends on both charge magnitude and the distance separated. The image above colors the atomic surface by partial atomic charge with red being negative and blue being positive. The extent of positive charge at the C atom is greater than at the H atoms, but the electropositive nature of the H atom cannot be comfortably ignored in trying to understand the molecular dipole moment in structures like acetone.

3.11 INTERMOLECULAR FORCES AND PHYSICAL PROPERTIES

(Arthur Cammers, 2019)

All intermolecular forces are electrostatic interactions that result from forces between opposite charges. Just as opposite point charges attract one another so do the tails and heads of dipoles. We would expect to find the C atom of one molecule proximal to the O atom of another on average in condensed phases (solids, powders, crystals, liquid-crystals and liquids); although the dynamic nature of the liquid will be much greater than any solid state. Properties such as solubility, boiling point, density, and melting point are affected by attraction between molecules.

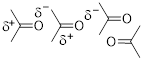
When solids melt, molecules in bulk phases move more quickly relative to one another. More cohesive molecules with stronger intermolecular forces tend to move less than those with weaker intermolecular forces. The abrupt state change from liquid to gas involves a large change in average intermolecular distances. Less cohesive substances boil at much lower temperatures than those with stronger intermolecular interactions. The intermolecular forces responsible for establishing molecular scale cohesion are listed below from weakest to strongest.

dispersion forces < dipole-dipole interactions < hydrogen bonding interactions

The next sections discuss these three types of intermolecular interactions.

3.11.1 Dispersion Forces

Dispersion is a weak force dependent on non-polar molecular surfaces, and –  likely due to early confusion about the nature of the force – it goes by a few names: London dispersion forces, ■ Van der Waals forcese, and ■ the Casimir Effect. This type of molecular cohesion is active at close distances. If we think about a molecule in real time, we know that electrons are in constant random motion within their orbitals and sometimes produce a distribution that is not evenly balanced with the positive charge of the nuclei. The result is a fleeting attraction between the two molecules a shown in the example of two molecules below.

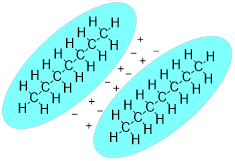
The phenomenon requires contact of molecular surfaces. Dispersive forces solidify candle wax, make diesel fuel freeze at a higher temperature than gasoline, and enable gecko lizards to defy gravity on ceilings and walls. This weak force is present in all molecules, but it is orders of magnitude weaker than other intermolecular forces. When the molecular structure does not permit much molecular surface area to make contact or when stronger intermolecular forces are present, dispersive forces in molecules are hidden. Since the carbon and hydrogen atom have similar electronegativities, their bonds are covalent and non-polar, so we expect dispersive forces to be the main intermolecular forces governing the properties of the hydrocarbons like the molecules below.

3.11.2 Dipole-Dipole Interactions

Fundamentally due to atomistic electronegativity, the nature of the interaction between permanent dipoles, a cohesive molecular force, is discussed above with acetone in the showcase. It is responsible for elevated boiling and melting points in small molecules and increases solubility and miscibility in other polar liquids. The magnitude of this force is stronger than dispersion.

3.11.3 Hydrogen Bonding Interactions

Hydrogen bonding is a strong type of dipole-dipole interaction with a more complex story that we will have to unpack in detail later. It also has a greater influence than dipole-dipole interactions on bulk properties. For now, let’s characterize molecules and solvents as either non-polar or polar, and protic or aprotic. These attributes are important to the ability of a ■ solvent to dissolve molecules. This one statement touches many aspects of many billion-dollar industries from the production of new cars to manufacture of bubble gum. Polar molecules have a molecular dipole, and the greater the dipole moment, the more polar the molecule. Non-polar molecules have small or zero molecular dipoles. Protic molecules have X−H bonds where X = elements of greater electronegativity than the C atom. Aprotic molecules have no X−H bonds and contain no hydrogen atoms connected directly to an electronegative atom.

When a hydrogen atom bonds with elements on the first or second row of the periodic table, an average dipole moment can be assigned to the bond. Furthermore, the bond possesses a level of ionic character.

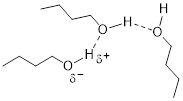
The positive and negative portion of the polar bond form partial bonds called hydrogen bonds (shown by the dotted line in the image above). These protic groups also allow increased molecular interaction with water.

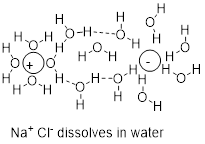
Because the O and H atom are so different in electronegativity, there is an ionic component to water, the classic protic solvent. Molecules of water can get between Na and Cl atoms in NaCl and thereby dissolve the salt as in the figure below.

A similar argument based on the strong polar interactions between water molecules rationalizes the solubilities of liquids in water. The solubility of a liquid in a liquid is referred to as miscibility. Besides perhaps an extensive experience with mixed alcoholic drinks, from the structure of ethanol you may also predict that ethanol and water should dissolve. You might also predict that the cohesive forces between water molecules should squeeze diethyl ether out of the aqueous bulk phase to force a bilayer in a mixture of the two liquids with the ether suspended above the water due to the difference in density. When we try to mix ethyl ether with water the effect is demonstrable.

The same argument explains why water and oil do not dissolve. Oil being, in general, a mixture of hydrocarbons will only have the weak dispersion forces available to it and will not interact favorably with water. Thus, between oil and water a bilayer forms in the mixture.

In Chapter 1 there was a discussion about isomers. The vastly different boiling points of two isomers of C₂H₆O were offered to showcase the fact that atomic constitution of molecules has a profound impact on molecular properties.

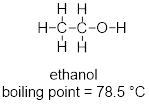
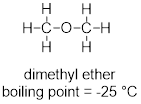
At this point you can inspect ethanol and dimethyl ether and identify the XH function in ethanol in the form of the hydroxyl group (OH). You can see that these strongly polar components don’t exist for dimethyl ether. You can envision how there is stronger interaction between the ethanol molecules in a liquid sample than there is between molecules of dimethyl ether in the liquid state, since the structure of the ethanol molecule makes hydrogen bonding possible and that of dimethyl ether does not.

Exercise 3.11.1 Identify whether each of the following compounds exhibits a molecular dipole moment. For compounds that do, indicate the direction of the net molecular dipole moment.

Exercise 3.11.2 Think about the dependence of surface area contact between molecules that would rely on dispersion and predict which 5-carbon hydrocarbons should boil at lowest temperature.

3.12 UV-VIS SPECTROSCOPY - A MINIMAL INTRODUCTION

(Arthur Cammers, 2019)

Like PES, UV-visible (UV-vis) spectroscopy is pertinent to the relative energies of MOs. However, instead of creating ions by ejecting electrons, quanta of UV and visible EM energy promotes electrons in molecules from HOMOs to unoccupied higher-energy MOs. This phenomenon has molecules absorbing energy from the EM field. In this case the molecule goes from the ground state to an electronically excited state. Excited state energy is emitted at longer wavelengths (lower energy light) or is lost to the sample as heat (non-radiative - or vibrational - decay of the excited state). In the latter case, the temperature of the material increases.

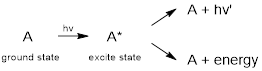
The spectroscopic technique requires instrumentation that can compare a reference beam of light to a beam of light that has been passed through the sample under study. By measure the two intensities as a function of wavelength, the instrument can plot a spectrum showing at which wavelengths the sample absorbs light. The longer the wavelength, the less difference in energy are the occupied MO from which the electron is promoted to the unoccupied MO where the electron exists in the excited state.

The effect of conjugation decreases the energy of π electrons due to the way antibonding and bonding is minimized and maximized, respectively. Conjugation also decrease the difference in energy between the HOMO and the LUMO in molecules. Since the energy gap of these transitions of the electron from HOMO to LUMO narrows with increasing conjugation, more conjugated molecules tend to absorb light at longer wavelengths. This phenomenon is explained by the familiar equation that relates the energy of electromagnetic radiation to frequency and wavelength using Planck’s constant of proportionality. In this case, ΔE is the difference between the energies of the HOMO and the LUMO.

ΔE = hv = hc /λ

where v = frequency of light, h = Planck’s constant, c = the velocity of light and λ = wavelength.

3.13 ANALYTICAL UV-VISIBLE SPECTRA and MO CONJUGATION

(Excerpt from Organic Chemistry with a Biological Emphasis, Timothy Soderberg, 2016)

• Places where Soderberg’s text refers to previous chapters and sections not shown here have been removed and indicated with: […].

• Places where Cammers adds to Soderberg’s text are indicated by [… added text]

• UV-visible (UV-vis) spectroscopy provides us with information about aromatic groups and other conjugated π systems in organic compounds. […]

3.13.1 The Electronic Transition

Recall from […] that molecular orbital (MO) theory can be a useful way to think about covalent bonding in molecules containing conjugated double bonds and aromatic rings. Keep in mind that molecular orbitals result from the mathematical combination of two or more atomic orbitals and describe a region in space around a group of atoms (rather than a single atom) in which electrons are likely to be found. We'll see here that MO theory is indispensable to a discussion of ultraviolet and visible spectroscopy.

A chromophore is any molecule or part of a molecule that has the property of absorbing light in the ultraviolet or visible region of the spectrum. 1,3-butadiene is a chromophore. Recall […] that the conjugated π bonds in1,3-butadiene can be pictured as four parallel, overlapping p orbitals sharing four electrons.

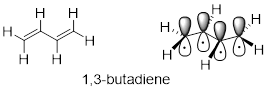
Using the language of MO theory, we can say that the four p atomic orbitals combine to form four π molecular orbitals. The two lower energy orbitals ψ₁ and ψ₂ are bonding orbitals, while the two higher energy orbitals ψ₃ and ψ₄ are antibonding orbitals.

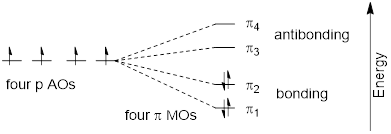
In the electronic ground state, all four π electrons in the conjugated system reside in the two bonding orbitals. A π→π* transition occurs when an electron in ψ₂, the highest occupied molecular orbital (HOMO) jumps up to ψ₃, the lowest unoccupied molecular orbital (LUMO). The gap between these two molecule orbitals is often called the HOMO-LUMO energy gap.

For 1,3-butadiene, the energy difference in the HOMO-LUMO gap is 552 kJ/mol. This energy corresponds to light with a wavelength of 217 nm, which is in the ultraviolet region of the spectrum. When a sample of 1,3-butadiene is irradiated with UV radiation, the molecule absorbs the light at 217 nm as an electron undergoes a π→π* transition.

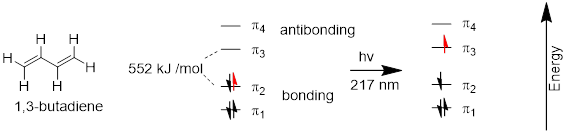
The absorbance due to the π→π* transition in 1,3,5-hexatriene occurs at 258 nm, corresponding to a HOMO-LUMO gap of 464 kJ/mol.

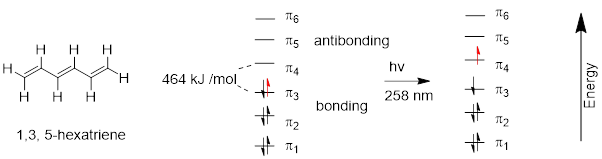
Notice what happened here: when the conjugated π system was extended by two carbon [atoms], the HOMO-LUMO energy gap shrunk from 552 to 464 kJ/mol. A lower energy transition corresponds to longer wavelength absorbance [… E and λ have an inverse relationship by ΔE = hv /λ]

As conjugated π systems become more extended,

a) the HOMO-LUMO gap shrinks, and

b) the wavelength of absorbed light becomes longer.

In molecules with very large, extended conjugated π systems, the π ® π* energy gap becomes so small that absorption occurs in the visible rather than the UV region of the [… ■ electromagnetic spectrum].

The visible region of the electromagnetic spectrum:

ß-carotene, with its system of 11 conjugated double bonds, absorbs light in a broad band between approximately 420-550 nm, with a λ_max at 470 nm, spanning the blue and green regions of the visible spectrum. Because blue and green wavelengths are absorbed while those in the red and yellow regions pass through the sample, ß-carotene appears to our eyes as orange. ß-carotene is abundant in carrots and is the compound mainly responsible for their orange color.

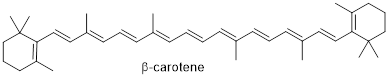
Exercise 3.13.1 What is the energy of absorption (in kJ/mol) due to light with wavelength of 470 nm, the λ_max of ß-carotene?

Exercise 3.13.2 Which of the following molecules would you expect absorb at a longer wavelength in the UV region of the electromagnetic spectrum? Explain your answer.

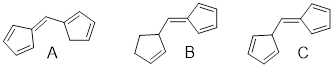
3.13.2 Protecting Yourself from Sunburn

Human skin can be damaged by exposure to ultraviolet light from the sun. We naturally produce a pigment called melanin, which protects the skin by absorbing much of the ultraviolet radiation. Melanin is a complex polymer. Two of its most common monomers units of are shown below.

Overexposure to the sun is still dangerous, because there is a limit to how much radiation our melanin can absorb. Most commercial sunscreens claim to offer additional protection from both UV-A and UV-B radiation. UV-A refers to wavelengths between 315-400 nm, UV-B to shorter, more harmful wavelengths between 280-315 nm. PABA (para-aminobenzoic acid) was used in sunscreens in the past, but its relatively high polarity meant that it was not very soluble in oily lotions, and it tended to rinse away when swimming. Many sunscreens today contain, among other active ingredients, a more hydrophobic derivative of PABA called [■ Padimate O].

3.13.3 Looking at UV-vis Spectra

We have been talking in general terms about how molecules absorb UV and visible light – now let's look at some actual examples of data from a UV-vis absorbance spectrophotometer. […] Radiation with a range of wavelengths is directed through a sample of interest, and a detector records the wavelengths where absorption occurs and to what extent. Below is the absorption spectrum of an important biological molecule called nicotinamide adenine dinucleotide, abbreviated NAD⁺. The adenine nucleotide base in the compound absorbs light in the neighborhood of 260 nm, which is within the UV range of the electromagnetic spectrum.

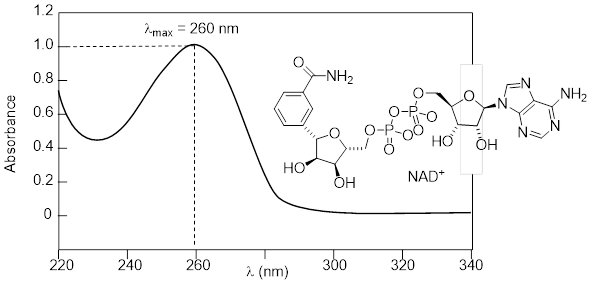
The convention in UV-vis spectroscopy is to show the baseline at the bottom of the graph with the absorbance bands pointing up […]. Wavelength values on the x-axis are generally displayed in nanometer (nm) units. On the y-axis is a measure of how much light was absorbed at each wavelength, expressed as absorbance (A). […] To calculate absorbance at a given wavelength, the computer in the spectrophotometer simply takes the intensity of light at that wavelength before it passes through the sample (I₀), divides this value by the intensity of the same wavelength after it passes through the sample (I), then computes the log₁₀ of that number.

A = log (I₀/I)

Note: In this expression the units cancel, so A is a unitless value.

Typically, there are two things that we look for and record from a UV-vis spectrum. The first is λ_max, the wavelength at maximum absorbance, which visually is the very top of the broad absorbance band. We also record the value of A at λ_max, which depends on the concentration of the sample [… and a constant of proportionality specific to the molecule of interest and the λ relating A to concentration, call the molar absorptivity, ε. A = εLc, where L = path length (cm) of transmitted light, and c = concentration of the ■ analyte]. The NAD⁺ spectrum above shows a maximum absorbance of 1.0 at 260 nm. In the next section, we will see how we can use this data to calculate the concentration of NAD⁺ in the sample.

Here is the absorbance spectrum of the common food coloring Red #3:

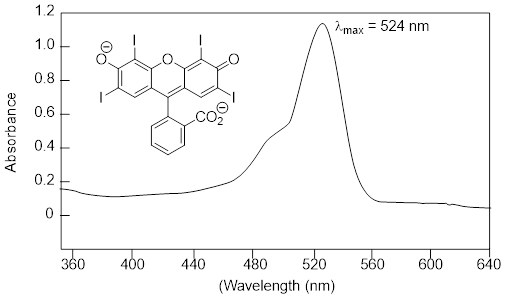
Here, we see that the extended system of conjugated π bonds causes the molecule to absorb light in the visible range - specifically, with a λ_max of 524 nm, which is in the blue/green range. Red wavelengths pass through without being absorbed, so the solution appears red to our eyes.

Exercise 3.13.3 What changes do you think should occur in the UV with the structural change from A to B below? Explain your answer.

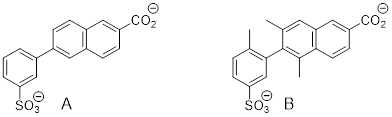
Now, take a look at the spectrum of another food coloring, Blue #1:

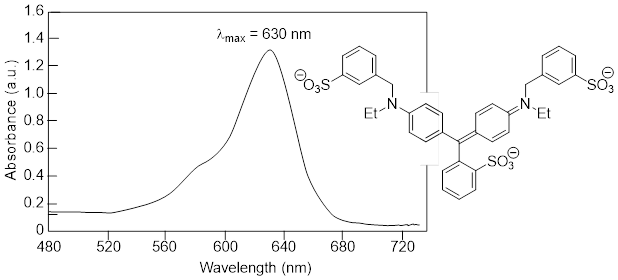
The maximum absorbance occurs at 630 nm, in the orange range of the visible spectrum, and the compound appears blue.

3.13.4 Organic and Biological Analytical UV Spectroscopy

UV-vis spectroscopy has many applications in organic and biological chemistry. The Beer – Lambert Law is often used to determine the concentration of a UV-active sample. You most likely have performed a Beer – Lambert experiment in a General Chemistry lab. The law is simply an application of the observation that, within certain ranges, the absorbance of UV-active compound at a given wavelength varies in a linear fashion with its concentration: the higher the concentration, the greater the absorbance.

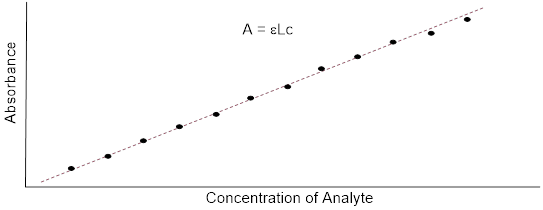
If, for a particular sample, we divide the observed value of A at λ_max by the concentration of the sample (c, in M) [… and the pathlength L], we obtain the molar absorptivity, or extinction coefficient (ε), which is a characteristic value for a given compound [… at λ_max] that we can [… often] look up.

ε = A/cL

In the above equation, 'L ' is path length - the distance that the beam of light travels though the sample - expressed in cm. Most sample holders are designed with a path length of 1.0 cm, so the conventional unit for molar absorptivity is L•mol^-1•cm^-1. In all UV-vis discussion or problems in this book, you should assume that the relevant path length is 1.0 cm.

For example: In the spectrum of NAD⁺ [… above], we see that A = 1.0 at λ_max of 260 nm. We look up the molar absorptivity of NAD⁺ at 260 nm and find that it is listed as ε(260) = 18,000 M^-1•cm^-1. Using [… The Beer Lambert Equation], it is easy to calculate that the concentration of the sample is 5.6 x 10^-5 M.

The bases of DNA and RNA are good chromophores:

adenine guanine cytosine thymine

Biochemists and molecular biologists often determine the concentration of a DNA or oligonucleotide sample by assuming an average value of ε(260) = 0.020 ng•L^-1•cm^-1 for double-stranded DNA at its ε_max of 260 nm (notice that concentration here is expressed in terms of mass rather than moles: nanograms per microliter is a convenient unit for DNA concentration when doing molecular biology).

Exercise 3.13.4 50 μL of an aqueous sample of double stranded DNA is dissolved in 950 μL of water. This diluted solution has a maximum absorbance of 0.326 at 260 nm. What is the concentration of the original (more concentrated) DNA sample, expressed in g/L?

Because the extinction coefficient of double stranded DNA is slightly lower than that of single stranded DNA, we can use UV spectroscopy to monitor a process known as DNA melting, an important factor in molecular cloning experiments. If a short stretch of double stranded DNA is gradually heated up, it will begin to ‘melt’, or break apart, as the temperature increases (recall that two strands of DNA are held together by a specific pattern of hydrogen bonds formed by ‘base-pairing’).

As melting proceeds, the absorbance value for the sample increases, eventually reaching a high plateau as all the double-stranded DNA has melted into two strands. The mid-point of this process, called the ‘melting temperature’, provides a good indication of how tightly the two complementary strands of DNA bind to each other.

[… end of excerpt from Organic Chemistry with Biological Emphasis, Timothy Sodeburg, 2019]

KEY TO CHAPTER 3 EXERCISES

(Susan Odom, Arthur Cammers, and Ashley Jolly Steelman 2019)

Exercise 3.3.1 Answer: In both structures, the C-H bonds are formed from an sp2 orbital from C and a 1s orbital from H.

Exercise 3.5.1 Answer:

(a)

(b) 3: heptyne, 2-heytyne, 3-heptyne

Exercise 3.5.2 Answer:

(a)

(b) 5: decyne, 2-decyne, 3-decyne, 4-decyne, 5-decyne

Exercise 3.5.3 Answer: (a) Molecule b is most basic (b) because the lone pair on the N atom is higher in energy than the other lone pairs on the N atoms in the other molecules. The electrons in b are the least stable because they have the least s character (25% s) due to sp³ hybridization. Molecule a has the lowest energy lone pair (50% s) and thus the least basic. (Remember s character stabilizes electrons; it decreases reactivity.)

(c)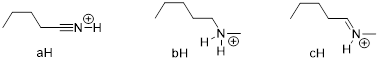

Note: In drawing you line structures remember the formal charges. If we add a charged species +H to a neutral molecule the product must be charged. Charge is conserved.

Exercise 3.5.4 Answer: 90°. See 3D model below.

The C2 and C6 are highlighted in yellow. The H atoms on C3 and C5 are highlighted in yellow. To make two π bonds the central C atom must use two orthogonal p orbitals (perhaps px and py) which puts the two σ bonds at this atom on the z axis, colinear. The C atoms attached to the central atom must make π bonds with px and py respectively, which puts their σ bonds on the XZ and YZ planes respectively, so the dihedral angle in question must be 90°.

Exercise 3.6.1 Answer: Only one lone pair and one π bond can interact at a time in the molecule.

Exercise 3.6.2 Answer: ψ2 in ozone should be lower in energy and thus less of an electron donor. This is due to the electronegativity of the O atom. Electronegativity always decreases the energy of MOs (bonding and antibonding) due to an increased ability of the atom to stabilize electrons. For a reaction that we will consider later, we’ll see that the O atom electronegativity brings ψ3 low enough in energy to function as an electron acceptor.

Exercise 3.6.3 Answer: The effect of electronegativity is much more pronounced in the lowest energy orbital, ψ1. The MO coefficients are redistributed as the number of nodes increases in the MOs. For example, in ψ3 the coefficients favor electron occupation at the least electronegative atom. What bonding orbital does, antibonding orbital reverses.

Exercise 3.7.1 Answer:

Exercise 3.7.2 Answer: Google: https://lmgtfy.com/?q=allyl+MOs+images

Exercise 3.7.3 Answer: Google: https://lmgtfy.com/?q=pentadienyl+molecular+orbitals+image

Exercise 3.7.4 Answer: Google: https://lmgtfy.com/?q=benzene+molecular+orbitals+images

Exercise 3.9.1 Answer: At each C atom there’s a π bond. A p orbital is necessary for it. That leaves one s and two p orbitals to use in σ bond construction, so these bonds are sp². Since the σ bonds get their directionality from the p orbitals used in their construction these bonds are coplanar. This question was solved by counting the p orbitals at the C atoms.

Exercise 3.9.2 Answer: At each C atom there are two π bonds. Two p orbitals are necessary for these, leaving one s and one p orbital to use in σ bond construction. The σ bonds (CC and CH) at the C atoms are sp hybridized. Since the σ bonds get their directionality from the p orbitals used in their construction these bonds are colinear; the molecule is linear. This question was solved by counting the p orbitals at the C atoms.

Exercise 3.9.3 Answer: At the N atom there are two π bonds. Two p orbitals are necessary for these. That leaves one s and two p orbitals to use in σ bond construction and in the hybridization of the orbital containing the lone pair so the CN σ bond at N and the lone pair are sp. This question was solved by counting the p orbitals at the N atom.

Exercise 3.9.4 Answer: (a) N1-H. (b) The N−H in the NH₂ group outside the ring has no pure p orbitals. All s and p orbitals are used in the three σ bonds and the lone pair. This group at the N atom is sp³ hybridized. The N1−H bond is 33% s character whereas the bonds and lone pair of the NH₂ group are only 25% s character. The N1−H bond is shorter due to having more s character (sp² vs. sp³). Shorter bonds are more stable, less reactive and at lower energy. This question was solved by counting the p orbitals at the N atoms.

Exercise 3.9.5 Answer: Redraw the structure to account for the electrons in lone pairs. Make sure you understand the nature of the question.

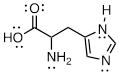
The N bound to two H atoms houses the most basic electron pair.

The highest energy electrons are the most basic electrons. Since There are lone pairs that are - by definition - not bonded, and we are not considering reactions with π bonds. The bonds will likely not be the source of electrons because bonds decrease the energy of electrons making them less reactive.

• The lone pairs on the oxygen atoms are relatively stable due to the relative electronegativity of the O atom compared to the N atoms. This effect renders the lone pairs on the O atoms less basic.

• The lone pair on N1 is in a p orbital but engaged in π bonding. Bonding of any kind stabilizes electrons (decreases the energy).

• The lone pair on N3 is contained by an sp² orbital since there is a π bond to the N atom.

• The unbound electron pair on NH₂ is contained by an sp³ orbital. These unbound electrons have the highest p character, and they are on a relatively electropositive atom (compared to the O atom). The NH₂ atom’s lone pair is therefore the most basic.

Exercise 3.9.6 Answer: In A the lone pair on the N atom has to be in a pure ‘unmixed’ p orbital due to π bonding with the CO π system. In B the lone pair on the N atom must be twisted out of conjugation with the CO π system. The lone pair and the NC bonds at the N atom in B are housed in sp³ hybridized orbitals. This question was solved by counting the p orbitals at the N atoms in A and B.

Exercise 3.9.6 Answer: a) the electron sit in a π* MO. b) there are no antibonding orbitals depicted in Lewis or line structures.

Exercise 3.11.1 Answer:

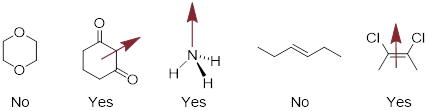
Exercise 3.11.2 Answer: Neo-pentane. It is the least linear (most branched) and therefore has fewer contact points. Think about the contact among several volley balls in a bin vs many noodles in a bowl.

Exercise 3.13.1 Answer: ΔE = hv = hc/λ = (6.63E-34 J•s)(2.999E17 nm•s^-1) / 470 nm • 6.02E23 / mol•kJ / 1000 J = 254.8 kJ•mol^-1

Exercise 3.13.2 Answer: A. It has more π bonds in conjugation. Between the two rings B is an sp³ hybridized C atom, which breaks the conjugation of the π bonds. In C, a the C in the CH group in the left ring is sp³ hybridized, breaking conjugation.

Exercise 3.13.3 Answer: B. It must hold the flat rings in a non-coplanar manner. The C-C-C-C dihedral angle > 0°. This twist the two rings out of conjugation and shortens λ_max and decrease the intensity of the absorption (molar absorptivity).

Exercise 3.13.4 Answer: 310 ng /L. Explanation: Assume an average value of ε(260) = 0.020 ng•L^-1•cm^-1 for double-stranded DNA at ε_max of 260 nm. A = ε(260)•c•L Assume that the same cuvette was used so the pathlength is the same. Concentration after dilution = 0.326 /0.020 ng•L^-1 = c = 16.3 ng•L⁻¹. The dilution factor was 50 / 950, so the concentration before dilution = 16.3 ng•L⁻¹ •950 /50 = 310 ng /L.

CHAPTER 3 PRACTICE PROBLEMS

(Ashley Jolly Steelman, Arthur Cammers, and Susan Odom, 2019)

PP 3-01 Methylene, CH₂, is a reactive species. (a) Draw the Lewis structure for CH₂. (b) Explain why this species is so reactive. (c) Given that there is an electronic variant of CH₂ that partially occupies MOs, how should the bond angles of CH₂ and CHOCH₃ differ? This question relates to an ■oxonium structure considered ■ previously. Should one be wider than the other? If so, which one is wider and what are these approximate values?

PP 3-02 You do not need the details here to apply the principles broadly. (Data provide by John Anthony, University of Kentucky, 2019)

The figure below shows the UV-vis absorption spectra of solutions of a series of acenes of variable conjugation length. The y axis (absorbance) indicates that the intensity of each spectrum is normalized, which means that the absorption intensity is not proportional to the ε values for each molecule.

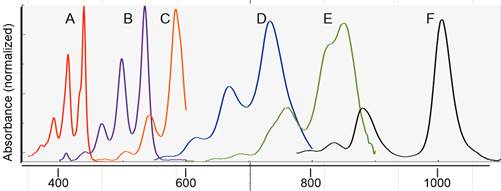
Wavelength(nm)

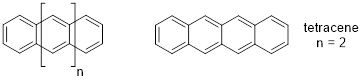
(a) Match the letter of the spectrum to the length parameter, n.

(b) What color would you expect for a solution of D? Explain your reasoning.

PP 3-03 Draw the π MOs for 1,3,5-hexatriene. Google the images of these. How close did you come to guessing them right? Some of the images will not try to modify the sizes of the atomic coefficients. Some people making these images are not aware that these change from MO to MO.

PP 3-04 (a) What is the hybridization at the C bound to H in the chemical species below? (b) What do you expect for the CCH bond angle?

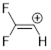
PP 3-05 As an undergrad. Dr. Cammers worked in the research laboratory at U. Wisconsin-Eau Claire. In 1985 his research mentor Dr. O made a comment about C atom electronegativity (EN) as a function of hybridization as part of a long-winded explanation of something else they were discussing. At the time he was a bit confused; he thought that EN was assigned to atoms period; how could EN change with atom hybridization? It’s amazing how a moment of wonder can solidify a memory—that spot in time was over three decades ago. The conversation had to stay focused, and Dr. Cammers never pursued this with him.

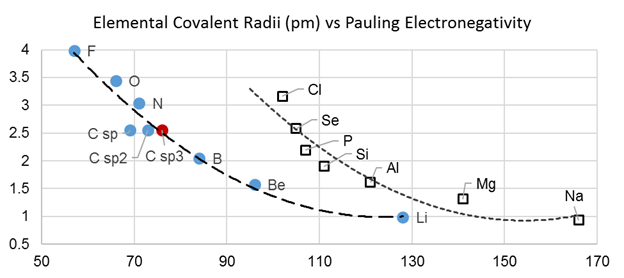
On the y axis are values for atomistic Pauling EN, and on the x axis are values for covalent radii. Notice that the covalent radii are different as a function of the hybridization of the bond at C, but the y axis values are identical because they are atomistic. Should EN change as a function hybridization, or should EN simply be an atom-specific number? Justify your answer.

PP 3-06 Referring to the graph above, covalent radii for N and O atoms as a function of hybridization of the covalent bond at the atom should be available, but I did not pursue these numbers for the problem above. Do you think that the covalent radius spread the points out as much for O and N atom as it does for the C atom? Explain your reasoning.

PP 3-07 Imagine you have been given pure sample of the two molecules A and B below, and you are trying to identify which is which using a UV-vis spectrometer. How would you identify which sample matched which structure?

PP 3-08 Dimethyl sulfoxide (DMSO) is a polar liquid that is miscible with water. Look up the structure of DMSO and show how it could interact with water molecules.

PP 3-09 For each pair of compounds, circle the compound with a higher boiling point. Then give a brief explanation for your choices.

PP 3-10 Structural elucidation: Determine the structure of an unknown compound using the following structural information.

· The molecular formula is C₄H₁₀N₂.

· UV-vis indicates there are no π bonds in the structure.

· The compound exhibits no net dipole moment.

· The compound exhibits hydrogen bonding with itself.

Hint: Calculate the degrees of unsaturation.

PP 3-11 DMSO has molecular dipole = 4.3 D. Determine which molecule is expected to most soluble in dimethyl sulfoxide (DMSO) and justify your answer.

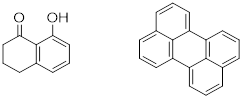
PP 3-12 For the three molecules drawn below, provide answers to the following.

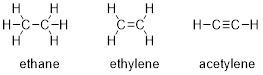
(a) What is the hybridization of the C atoms in ethane? _____ ethylene? ______ and acetylene? _____

(b) What kind(s) of orbitals are used to form π bonds in ethylene and acetylene?

(c) Which molecule has the shortest C-C bond?

(d) Which molecule has the shortest C-H bond?

(e) Which molecule contains the most acidic protons?

PP 3-13 Determine the name of the structures below.

PP 3-14 Single bonds generally experience free rotation at room temperature.

Nevertheless, the “single bond” shown below exhibits a large barrier to rotation. In other words, the energy of the system is greatly increased if the bond is rotated. Explain the source of the energy barrier.

PP 3-15 Which of the following alkanes would have the highest boiling point? Briefly explain why.

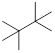
PP 3-16 Depict the direction of each molecule’s molecular dipole moment if one is present.

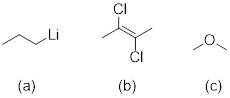
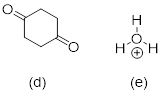
PP 3-17 Identify the hybridization of the σ bonds of each identified atom in acetylsalicylic acid (Aspirin).

PP 3-18 Explain why the following isomers have different boiling points.

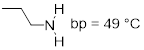
PP 3-19 Think about two isomers of the formula C₃H₈O₂, one with this connectivity: A) C─O─C─O─C and the other with this connectivity: B) O─C─C─C─O. a) Which one is more water soluble? b) Which one has the lowest boiling point? c) Which one has the lowest melting point? d) Is one more polar than the other?

KEY TO CHAPTER 3 PRACTICE PROBLEMS

(Susan Odom, Ashley Jolly Steelman, and Arthur Cammers 2019)

PP 3-01 Methylene, CH₂, is a reactive species.

Methylene is a reactive species because it has an empty orbital.

Triplet methylene partially occupies AOs, whereas singlet methylene does not.

Geometry questions are answered by determining how the σ bonds are hybridized at the atom in question.

For the triplet the singly occupied orbitals are mostly p in character; this makes the C─H σ bonds at C mostly sp in character so the triplet has a wide HCH bond angle, ~180°.

The singlet will leave the empty orbital as a pure p orbital and hybridize the lone pair and the two CH bonds sp2, so the singlet has a narrower HCH bond angle, ~120°.

PP 3-02 Answer:

n = 1, A; n = 2, B; n = 3, C; n = 4, D; n = 5, E; n = 6, F

Other than the fact that the line of the spectrum is blue-ish … the answer is blue. But instead of just telling you the answer, perhaps it is better to tell you how you could have sorted it out yourself. Step one: what wavelength is mostly being absorbed? Looking at the spectrum, it looks like about 725 nm. Step two: What color does this correspond to? Googling the ■ visible spectrum (Wikipedia page) 725 corresponds to red color. Step three: Realize that white light has all the colors. If a color is missing from the white light the light will look like its ■ compliment. Light passing through this sample and entering our eyes will appear cyan.

PP 3-03 Answer: https://lmgtfy.com/?q=molecular+orbitals+for+hexatriene

PP 3-04 Answer: (a) sp², (b) 120°

PP 3-05 Answer: EN certainly changes as a function of sigma bond hybridization and perhaps should be orbital-specific instead of atomistic. At this point we know that the π bond holds electrons less tightly than σ bonds, for example. Greater s character in bonds must increase EN. However, in current usage EN refers to atoms and serves as a rough guide for bond polarity and molecular interactions. The hybridization layer of complexity likely would render EN less useful for that purpose.

PP 3-06 No, according to the graph, the range of covalent radii as a function of EN appears to be decreasing because the slope of the curve appears to be increasing. For example, as O changes the way it hybridizes bonds, the bond lengths apparently should change less than they do when C changes the way it hybridizes bonds.

PP 3-07 Answer: Molecule B will absorb at a higher wavelength (lower energy) than molecule B due to the conjugation of the C=O and C=C bonds.

PP 3-08 Answer:

DMSO is a good hydrogen bond acceptor but it down not possess hydrogen bonds to donate. The partially positive charges on DMSO are on the C and the H atoms because these are the most electropositive, however these are not protic due to the fact that C and H are not very different in EN.

PP 3-09 Answer:

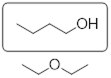
First set: Linear molecules have a higher b.p. than their branched isomers due to a greater number of intermolecular interactions in linear molecules.

Second set: The alcohol (top molecule) undergoes intermolecular hydrogen bonding whereas the ether (bottom molecule) does not.

Third set: The larger number of atoms in the second molecule leads to a greater number of intermolecular interactions than in the lower molecular weight molecule.

PP 3-10 Answer:

PP 3-11 Answer:

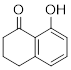
This molecule has both non-polar and polar bonds, like DMSO.

PP 3-12 Answer:

hybridization of C atoms in ethane: sp³, ethylene: sp², acetylene: sp

PP 3-13 Answer:

PP 3-14 Answer: The C2-C3 bond in the cation is not a single bond. This is an allylic system, which cannot be adequately represented by a single resonance structure. Both resonance structures and the resonance hybrid show that the conjugated system is spread over C1 through C3.

PP 3-15 Answer: The linear molecule (the left molecule, octane) has the higher boiling point because it has more intermolecular interactions than its branched isomer.

PP 3-16 Answer:

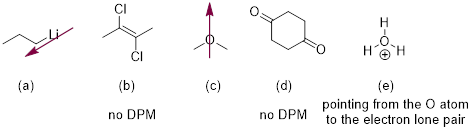
PP 3-17 Answer:

PP 3-18 Answer: The first isomer, (CH₃)₃N, cannot undergo hydrogen bonding. The second isomer, CH₃CH₂NHCH₃ can undergo hydrogen bonding, and the last isomer, CH₃CH₂CH₂NH₂ has even more hydrogen bonding interactions than the second isomer.

PP 3-19 Answer:

a) Which one is more water soluble? B due to hydrogen bonding.

b) Which one has the lowest boiling point? A due to lack of hydrogen bonding

c) Which one has the lowest melting point? A due to lack of hydrogen bonding

d) Is one more polar than the other? B is more polar. You might think that you can align the bond dipoles so that they cancel if you play with the conformation of B, but at some point if the (‑)O─H(+) dipoles get far enough apart they behave independently.