CHAPTER 4. ISOMERS AND
MOLECULAR CONSTITUTION
(Arthur Cammers, Ashley Jolly Steelman, and Susan Odom, University of Kentucky, 2019, with excerpts from Timothy Soderberg, “Organic Chemistry with a Biological Emphasis,” 2016)
Learning Objectives:
1.
Assemble and name
molecules according to IUPAC nomenclature.
2.
Be familiar with
the phenomenon of IR spectroscopy.
3.
Know
characteristic IR absorptions and be able to use this in analysis of IR
spectra.
4. Use the Cahn-Ingold-Prelog system (R/S) to assign
configuration at a chirality center.
5.
Understand enantiomers
have the same physical properties in achiral environments.
6.
Understand that living systems are chiral and
generally optically pure environments.
7. Understand
diastereomers and diastereomeric relationships have different physical
properties. Diastereomers can often be separated from another.
8. Understand
how enantiomers are separated.
9. Put
enzyme catalysis in terms of diastereomeric relationships.
10. Determine the stereoisomeric relationship between two
compounds.
11. Understand
the concept of optical rotation and
the definition of specific rotation.
12. Be able to convert %ee to fractions of
enantiomers.
13. Be able to calculate the %ee or isomeric fractions
given [α]D and observed αD.
4.1 INTRODUCTION: SOURCES AND USES OF ALKANES
(Susan Odom, 2019)
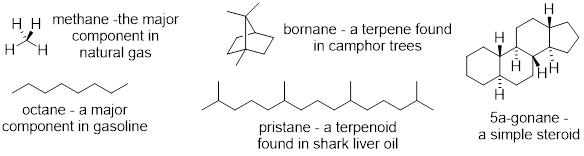
Alkanes, or hydrocarbons are saturated molecules that contain only carbon and hydrogen atoms. The simplest alkane is methane, CH4. Methane and other alkanes are most commonly isolated from natural gas and crude oil, although traces of methane found in the Earth’s atmosphere are produced by methanogenic microorganisms found in the guts of ruminants (e.g. cows). While alkanes generally have little biological activity, plants and animals produce alkanes that serve as oils, pheromones, and steroids.
Alkanes are used as fuels: combustion of alkanes by reaction with oxygen gas forms carbon dioxide and water, releasing energy. Alkanes are also used as feedstocks in chemical industries. As we will soon see alkanes can be modified by treatment with halogens and halogen-containing reagents (i.e. Cl2, Br2, and HBr) to introduce functional handles that are useful in the transformation of alkanes into useful chemicals for a variety of pharmaceuticals, cosmetics, plastics, and pesticides.
4.2 NOMENCLATURE
(Ashley Jolly Steelman and Susan Odom, 2019)
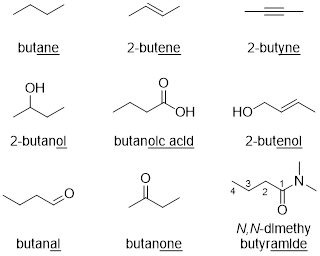
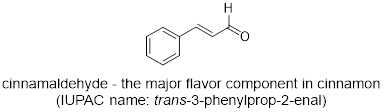
When some of the first molecules were discovered, chemists named them using, what we now call, common names. These common names, like cinnamaldehyde, often came from the compound’s unique properties like in this case the compounds smell/taste.
As the development of new molecules multiplied, it was decided that a systematic method for naming was needed. The International Union of Pure and Applied Chemistry (IUPAC) devised a system for naming organic compounds. This systematic method for naming compounds is important for communicating in organic chemistry. Common names lack structural details about a molecule; however, the IUPAC name tells people what type of molecule and/or functional group is present. The IUPAC name, (E)-3-phenylprop-2-enal, tells us exactly where the alkene and aldehyde are located on the benzene ring.
4.2.1 Naming Functional Groups
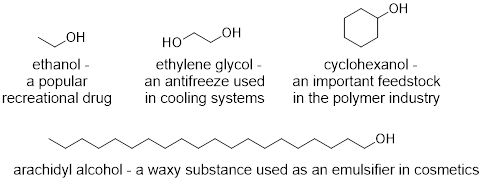
■ Functional groups are characteristic atoms bound together in a pattern that leads them to have similar reactivity. Remember that C and H atoms have similar electronegativities and that when these atoms are bound together, the molecular interactions are limited to weak dispersion. When other atoms of electronegativities quite different to C and H are combined in a molecule, we can predict their characteristic reactivities. Thus, it makes sense to name alcohols by their OH group even though there may be twenty C atoms and only one O atom in the molecule. Some examples of alcohols are shown below. In each case, there are C-C and C-H sigma bonds along with C-O and O-H sigma bonds. All are requirements to categorize a molecule as an alcohol.
The rules for naming organic compounds apply to all functional groups. The main difference in the name will be the suffix and this depends on what functional groups are present and which one takes priority. Examine the table and following examples. The table shows how the ending of each molecule’s name changes depending on the functional groups present, with the highest priority functional groups at the top.
Let us look at an
example of a compound that bears two functional groups that are not alkanes.
![]()
The molecule contains an alkene and an alcohol. According to the table, the alcohol takes priority as part of the parent chain and the name should end with the suffix “–ol”. The IUPAC name of the molecule is ■ but-2-en-1-ol, or 2-butenol. We can omit the number 1 because a lack of numbering for the alcohol implies that the OH group is positioned on the C having the lowest number in the parent alkyl (or alkenyl, in this case) chain. We will take the next couple of sections to explore the IUPAC system for naming in more detail.
|
Functional
Group |
Suffix |
|
|
carboxylic
acid |
-oic
acid |
|
|
anhydride |
anhydride |
|
|
ester |
-oate |
|
|
amide |
-amide |
|
|
aldehyde |
-al |
|
|
ketone |
-one |
|
|
alcohol |
-ol |
|
|
alkene / alkyne |
-ene / –yne |
|
|
alkane |
-ane |
4.2.2 IUPAC Nomenclature
The rules for deciphering the name of an organic compound are below. You should utilize these rules for all types of functional groups; however, here we will focus on learning the rules using alkanes. We will start with the following molecule as an example.
![]()
Naming an organic compound starts with identifying the longest carbon chain, this is termed the ‘parent chain’. You have previously studied the names of alkanes of carbon chains 1-10 atoms long. We will utilize this knowledge and build on it. If you count carbons on the structure below you will find that the highest number of consecutive carbons is six and therefore, our parent name will be hexane.
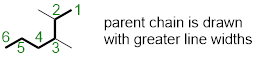
Identify and name the substituents. A substituent is an atom or group of atoms that replaces one or more hydrogen on the parent chain. If a substituent is composed of solely carbon atoms, we will utilize the prefix shown and add the ending with “–yl”. We see that each substituent bears only one carbon, so we call them methyl substituents. Attached to hexane the two methyl substituents are highlighted.
|
# of Carbons |
Prefix |
|
# of Carbons |
Prefix |
|
1 |
meth- |
|
6 |
hex- |
|
2 |
eth- |
|
7 |
hept- |
|
3 |
prop- |
|
8 |
oct- |
|
4 |
but- |
|
9 |
non- |
|
5 |
pent- |
|
10 |
dec- |
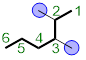
Note: When numbering the parent chain, you should give the substituents the lowest numbering possible. The structure labeled correctly, places the two methyl substituents on carbons 2 and 3 of the parent chain which is the lowest numbering possible for this compound.
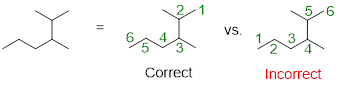
Lastly, we need to arrange the substituents alphabetically. If we have two or more identical substituents then the number of times the substituent occurs is indicated by a prefix di-, tri-, tetra-, penta-, hexa-, hepta-, etc. and a comma is used to separate position numbers. The complete name of the molecule is 2,3-dimethylhexane.
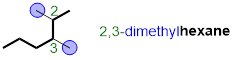
Note: A hyphen (-) is utilized in nomenclature to separate numbers from letters.
Let us practice with a different functional group.
Example 4.2.1
Determine the IUPAC name for the following molecule.
![]()
Solution
Step 1. We first need to locate the parent chain. The highest priority functional group needs to be a part of the parent chain, in this case the alkene. We also want to make sure that our alkene has the lowest numbering possible. The parent chain is made up of 7 carbons and is an alkene: heptene.
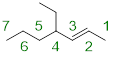
Note: We do need to clarify on which of the 7 carbons our double bond begins. In order to do this, we look at the carbon number of where our double bond starts, and in this case, we have 2-heptene.
Step 2. We locate any substituents attached to the parent chain and name them. The only carbons not accounted for in the parent chain is a two-carbon chain attached to carbon 4. Since the substituent contains two carbon atoms, we call it an ethyl group.
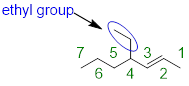
Step 3. Since we only have one substituent, all that is left to do is to add the pieces together to name it 4-ethyl-2-heptene.
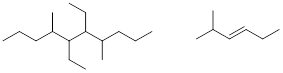
Exercise 4.2.1 Use IUPAC rules to name the molecules drawn below.
4.2.3 Molecules with Substituents Other than Carbon
|
Substituent |
Prefix |
Substituent |
Prefix |
Substituent |
Prefix |
Substituent |
Prefix |
|
F |
fluoro- |
OH |
hydroxy- |
Br |
bromo- |
NO2 |
nitro- |
|
Cl |
chloro- |
CN |
cyano- |
I |
iodo- |
NH2 |
amino- |
How do we name substituents other than carbon? One prominent class of molecules are alkyl halides (or haloalkanes), a class of molecules where one or more hydrogen atom of an alkane has been replaced with a halogen (F, Cl, Br, or I). Alkyl halides are commonly utilized in everyday life as well as very useful precursors in organic synthesis (a topic that we will discuss in a future chapter).

There are several other substituents that arise often in organic chemistry, and you should spend some time getting familiar with them. Recall that the same IUPAC rules will apply to all functional groups.
Example 4.2.2
Determine the IUPAC name of the following alkyl halide.
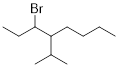
Solution
Step 1. We locate the parent chain. We want to make sure that our substituents have the lowest numbering possible. The parent chain is made up of 8 carbons and is an alkane: octane. Numbering the alkane from left to right puts our substituents on C3 and C4.
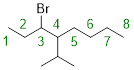
Step 2. We now need to locate any substituent attached to the parent chain and name them. The only substituents not accounted for on the parent chain is a bromine atom attached to carbon 3 and a branched alkane made up of three carbons attached to carbon 4.
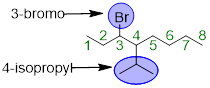
Note: If carbon substituents bear three carbons or more
then they can be branched instead of linear. These more complex substituents
have common names to help with the ease of using them in nomenclature. The
substituent that is present in the example above is isopropyl (a branched
three-carbon chain).
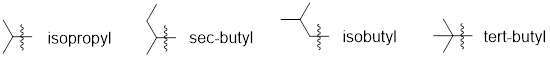
Step 3. Now we need to add the pieces together. Since the letter B comes before the letter I in the alphabet, we should recognize the bromine (“bromo”) substituent first, then name the compound as follows: 3-bromo-4-isopropyloctane.
Exercise 4.2.2 For the following molecules, determine which functional group would be the highest priority controlling the name of the parent chain. You should not take time to name the structures, they are quite involved. If you see the name, you know enough at this point to have some idea about what the structure has in terms of functional groups.

Exercise 4.2.3 Draw bond-line structures for (a) 2,4-dibromopentane and (b) 3-isopropyl-2,6-dimethylheptane.
4.2.4 Cyclic Molecules
The term “cyclo” is used to indicate the presence of a ring in the parent name. For example, if a ring contains three carbon atoms, then we place the term “cyclo” in front of propane and call it cyclopropane. Examples of rings containing three to eight carbon atoms are shown below.
 Once again, we can use the same rules above to name
substituted cycloalkanes. If there is only one substituent attached to the
ring, there is no need to number the point of attachment. If a ring contains
more than one substituent, then you need to number the ring beginning with the
lowest alphabetical substituent to differentiate the molecule from other
possible isomers. The parent chain of the molecule below is cyclopentane. We
see two substituents attached to the parent chain, a methyl and a bromo substituent.
Since B comes before M in the alphabet, we begin our
numbering with bromine, and count to minimize the number given to the next
substituent.
Once again, we can use the same rules above to name
substituted cycloalkanes. If there is only one substituent attached to the
ring, there is no need to number the point of attachment. If a ring contains
more than one substituent, then you need to number the ring beginning with the
lowest alphabetical substituent to differentiate the molecule from other
possible isomers. The parent chain of the molecule below is cyclopentane. We
see two substituents attached to the parent chain, a methyl and a bromo substituent.
Since B comes before M in the alphabet, we begin our
numbering with bromine, and count to minimize the number given to the next
substituent.

Example 4.2.3
Determine the IUPAC name for the compound shown.
![]()
Solution
Now our parent chain is not only a ring but also contains an alkene functional group. As the rules state the alkene takes priority within the ring so we just need to change the “–ane” suffix to “–ene”, from cyclopentane to cyclopentene.
You might also note that there is a substituent attached so we must determine the numbering for this molecule. Recall, the numbering of the highest priority functional group needs to have the lowest possible number. Therefore, we should start counting at the carbon of the alkene that makes the alkene C1 and C2. The overall name of the molecule will be 3-chlorocyclopentene.

Note: If there is an alkyl carbon chain that has a greater number of carbons than the cycloalkane, then the alkyl chain will be the parent chain. The cycloalkane will then act as a substituent to the alkyl chain. The name of the ring will have an ending "-yl" and, therefore, must be named as a cycloalkyl.
You have probably begun to notice the utility of IUPAC nomenclature. Let us look at one more example.
Example 4.2.4
Determine the IUPAC name for the compound shown.
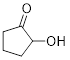
Solution: The molecule contains a ketone and an alcohol functional group. According to the priorities, the ketone takes the highest priority as part of the parent chain, and thus the parent name should be cyclopentanone. The only additional step is to describe where the hydroxyl group is located with the lowest numbering possible.
Exercise 4.2.4 Use IUPAC rules to name the molecules drawn below.

4.2.5 Bicyclic Molecules
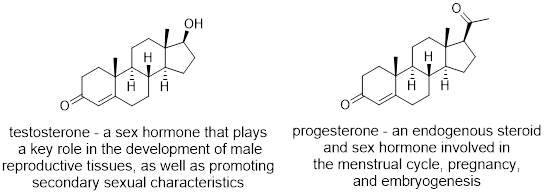
One of the more challenging functional groups to name are bicyclic molecules. Bicyclic compounds contain two rings fused together. A prominent example of this type of functional group can be seen clearly in steroids. Many people think of steroids as only being anabolic steroids; the synthetic variations of the male sex hormone, testosterone (also known as Juice or Roids). The chemical definition for steroid is much broader and is any class of natural or synthetic organic compounds characterized by a molecular structure of 17 carbon atoms arranged in four rings. A couple examples of this multi-cyclic system is found in testosterone and progesterone, both of which occur naturally in the human body.
Bicyclic systems can be divided into three major categories.
· spirocyclic compounds: contain two rings that share a single atom – often a quaternary carbon (quaternary meaning a carbon to which four carbon atoms are bound)
· fused bicyclic compounds: two rings share two adjacent atoms, meaning that two rings share one covalent bond.
· bridged bicyclic compounds: two rings share three or more atoms, with a bridge containing at least one atom separating two bridgehead atoms
Simple examples of each category of bicyclic systems are
shown below with their common names.

Exercise 4.2.5 What kind of bicyclic compounds are the steroids testosterone and progesterone?
Next we will learn the rules for IUPAC nomenclature for each type of compound.
Example 4.2.5
Provide the IUPAC name for spirobicyclohexane, a spirocyclic compound.
![]()
Solution
We name spirocyclic compounds in the following way:
“spiro[#A.#B]XXXane”, where
spiro indicates that two cycloalkanes are connected at one carbon atom
#A = the number of C atoms in one ring minus one
#B = the number of C atoms in other ring minus one
- If the rings are of unequal sizes, put the larger number second
XXXane = the name for the alkane containing the total number of C atoms in both rings, including the spiro carbon
In spirobicyclohexane, the #A and #B are both 6 – 1 = 5, so in brackets, we will use “[5.5]”. For the alkane, there are 11 C atoms total in the ring system, so we will use undecane. That gives us the name spiro[5.5]undecane.

Example 4.2.6
Provide the IUPAC name for decalin, a fused bicyclic compound.
![]()
Solution
We name fused bicyclic compounds in the following way:
“bicyclo[#A.#B.#C]XXXane”, where
Bicyclo indicates that two cycloalkanes share one covalent bond
#A = the number of C atoms connected to the bridgehead carbons in the longest chain
#B = the number of C atoms connected to the bridgehead carbons in the 2nd longest chain
#C = the number of C atoms connected to the bridgehead carbons in the shortest chain
- For a fused bicyclic compound, this will always be 0 because there is no third chain
- If the rings are of unequal sizes, put numbers in order from largest to smallest
XXXane = the name for the alkane containing the total number of C atoms in both rings, including the carbon atoms in the shared covalent bond
First find the bridgehead carbons. In the example below, they are marked in black/gray circles.
![]()
Next, identify the number of carbon atoms that are connected to the bridgehead carbon atoms – up to three rings in total. In decalin, #A (green) and #B (blue) are both 4, and there is no third ring, meaning that #C = 0, Thus, the numbers in the brackets will be [4.4.0]. The total number of carbons in the ring system is 10, making the XXXane name decane. Putting “bicyclo” at the beginning gives us a name of bicyclo[4.4.0]decane.

Example 4.2.7
Provide the IUPAC name for norbornane, a bridged bicyclic compound.
![]()
Solution
We name bridged bicyclic compounds using the same rules as the fused bicyclic compound in the previous example:
“bicyclo[#A.#B.#C]XXXane”
First find the bridgehead carbons. Afterward you can label the carbon atoms that belong to #A, #B, and #C. In the example below, the bridgehead carbon atoms are labeled in black/gray
![]()
In norbornane, #A (green) and #B (blue) are both 2, #C (red) is 1, meaning that the numbers in the brackets will be [2.2.1]. The total number of carbons in the ring system is 7, making the XXXane name heptane. Putting “bicyclo” at the beginning gives us a name of bicyclo[2.2.1]heptane.

Let us practice with another example of a bridged bicyclic compound, considering priority in naming when we have two bridgeheads and three different bridging rings.
Example 4.2.8
Provide the IUPAC name for the following bridged bicyclic molecule.
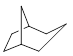
Solution
There are minor differences when it comes to numbering the parent chain for a bicyclic molecule. Here, we know that the parent chain has 8 carbon atoms and the “XXXane” part of the name will be octane.
Next, we want to identify the bridgehead carbon atoms and label them.

We then need to describe how the bridgeheads are connected. To each bridgehead, we have 1, 2, and 3 carbon atoms. When we name the molecule, the rules state that these numbers should be placed in brackets and specified from highest to lowest, [3.2.1].
In order to classify this molecule as a bicyclic structure we will always place the prefix bicyclo at the start of our name. This gives us a name of bicyclo[3.2.1]octane.

Exercise 4.2.6 Draw line structures that match compounds given the following IUPAC names.
bicyclo[2.2.0]hexane
bicyclo[2.2.2]octane
spiro[2.2]pentane
Exercise 4.2.7 Use IUPAC rules to name the following molecules.

4.3 INFRARED SPECTROSCOPY
(Arthur Cammers, 2019)
As we are beginning to examine multiple bonds to different atoms, IR spectroscopy becomes a talking point because this technique is most often used for functional group identification and the characterization of molecules.
We saw previously that in UV-vis spectroscopy, electrons in molecules are displaced and molecular excited states are reached, but the corresponding frequencies pertain to the movement of electrons sloshing around very quickly in molecules. Since electrons are fast compared to nuclei, when the frequency of the EM radiation is high the electrons move, with less change in nuclear position. The resonant frequency of IR is lower than UV-vis. Have a glance at the ■ EM spectrum to confirm. IR and UV-vis phenomenon are the same in that absorption of light promotes molecular excitation and the movement of electron density, but in the IR the frequencies of electronic displacement are low enough to involve the displacement of nuclei relative to one another in a molecule. For this reason, people also call IR spectroscopy, vibrational spectroscopy. Like in UV-vis spectroscopy, the ■ Beer-Lambert law holds for absorbance in IR.
There are various ways to collect IR data of molecules; they all involve the measure of the absorption of light by a sample containing the analyte. The operational aspects of sample preparation and instrument use can wait for the laboratory, a more advanced class in instrumental analysis, or advanced organic spectroscopic molecular identification. Here we will focus on enough of the theory to make some sense out of characteristic IR spectra.
4.3.1 IR Spectra: Absorption Intensity
The CO2 molecule strongly absorbs in IR frequencies; since increased CO2 concentration in the atmosphere is a by-product of burning hydrocarbons, we have been making an increasing impact on global temperature from the beginning of the industrial revolution, and ever more so with increasing population.
In CO2, the motion of the C atom relative to the O atoms in the molecule take electron density with the nuclei, thereby redistributing electron density (fluctuating charge), and therefore can interact with the EM field. As the term vibrational spectroscopy indicates, atomic displacement in molecules accompanies dynamic electronic displacement (dipole moments). This occurs when bonds stretch or bend, and atomic centers pyramidalize; however, the atomic motion must produce a net change in dipole moment. These vectors follow the electron density in the molecule as the O and C atoms move relative to each other.
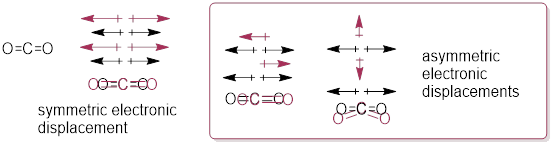
Asymmetric modes of molecular vibration in CO2 absorbs hv but the symmetric mode does not. The asymmetric modes involve a local fluctuation in the dipole moment. The dipoles in the symmetric electronic displacements are pulling one another the same amount in opposite direction and therefore, they cancel one another. You can perhaps visualize the IR-active molecular vibrations ■ here (choose controls and ‘play back and forth’).
The efficiency of a bond at absorbing IR radiation depends on strength of that molecule’s dipole moment. We can expect molecules with dipole moments, like acetone, discussed in the last chapter, to absorb strongly in certain regions of the IR spectrum. To the list of molecular properties that might absorb IR, we must add protic molecules, those with electronegative atoms bound to one or more H atoms.
Since C and H have similar electronegativities you might expect the CH motions to produce weak absorption in the IR spectrum. However, since s character increases in the C atom and this involves an increase in electronegativity, we will find that we can see relatively strong signals for most CH bonds. The C─H stretches in the following molecules absorb more strongly in the IR as we proceed from left to right below, in which R is some alkyl chain.
CH3CH2─R H2C=CH─R HC≡C─R
We will also notice the trend below, the stretching in the symmetrical triple bond on the left absorb weaker in general, than the stretching in the electronically asymmetric molecules.
R─C≡C─R (often invisible) HC≡C─R (medium) :N≡C─R (strong)
4.3.2 IR Spectra: Absorption Frequency
Generally, in producing a spectrum we graph intensity with frequency (think back on the PES and UV-vis spectra). The section above discusses the factors that cause molecules to strongly absorb IR radiation. In this section, we focus on the factors that determine the frequency of the absorption resulting in bands or peaks in the spectrum. The equation describing how frequency, force constant and mass relate in harmonic oscillators models the phenomenon fairly well.
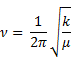
And because of the following relationship
ν = c /λ
we can surmise the following relationship.
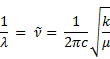
The equation can be put in terms of wave numbers, and we will see that the x-axis of the IR spectrum is put in units of wavenumber (cm−1). We are not interested here in calculating exactly which wavenumbers certain stretches and bends absorb on the spectrum. We are mostly interested in interpreting IR spectra so we have less to remember. To accomplish this, we will have to wrestle with the meaning of k and μ in the equation above. One inversely affects the wave number, and the other has a direct effect on the wavenumber.
4.3.3 IR Spectra: Bond Strength
In the equation for the IR absorption frequency, k roughly relates to bond strength. The correlation is not exact, but it is pretty good. For the harmonic oscillator, k is called the force constant and it expresses how stiff the vibrating spring is or how tight the guitar string is stretched. You know that the frequency with which the guitar string vibrates is a direct function of how tight it is set on the instrument. Stronger bonds also tend to have higher frequencies and thus, higher IR wave numbers. In the C─H stretches below, we would expect that the stronger triple bond will vibrate at higher frequencies (higher wavenumber) than the weaker single bond. We see that bond strength varies directly with s character. Indeed, the sp3-hybridized C-H stretch lies between 2652-2972 cm−1 (25% s); the sp2-hybridized C-H stretch (33% s) lies between 3000-3100 cm−1; and the sp-hybridized C-H (50% s) lies between 3280-3340 cm−1.
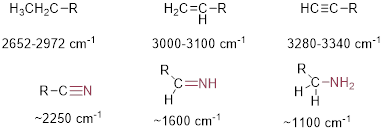
Can you guess which CO stretch is higher in wavenumber, the C=O in ketones or the C─O in alcohols? Of course, the double bond is stronger than the single bond. The C=O is very characteristic in IR spectra, and it is difficult to miss due to the fact that it is strong and appears between 1680-1820 cm−1. The ranges for C=O bonds in certain functional groups are smaller, but these details are a tour de force in memorization. Know that this information is just a few keystrokes away with an internet connection.
4.3.4 IR Spectra Atomic Mass
Certainly, our intuition has us thinking that the atomic mass of an atom will also play a role in where absorptions appear in the IR spectrum. We find that when more massive atoms vibrate slower in bond stretching (having lower wavenumbers) and smaller atoms vibrate at higher frequencies (having higher wavenumbers).
The μ factor in the equation above expresses this effect. The results are only exact for diatomic gasses because those masses are not bound to other atoms that complicate the phenomena by turning the two-body problem into a multibody problem, which becomes mathematically intractable quite abruptly. The reduced mass is, μ where
μ = m1•m2 /(m1 + m2)
Notice that the units are still in terms of mass.
![]()
This factor has the greatest effect on absorptions in the IR spectrum for atomic masses that are very different, like C, N, O, S versus the H atom. Notice the 800 cm−1 drop as the bond changes from C─H to C─D; this is expected since D is twice the mass of H. In this case nothing changes in terms of the chemistry of the bond since D and H are isotopic; the H / D effect is purely the impact of nuclear mass. The fact that lower μ values increases the wavenumber is the reason you will find C─H, N─H, O─H stretches at high numbers in the spectrum. However, their wavenumber values increase in this order due changes in bond strength.
4.3.5 IR Spectra: Absorption Band Width
In addition to intensity, and wavenumber another characteristic that becomes evident in IR absorption bands is how broad or narrow they are. The number of different structural states, and the bond vibration energies that accompany them, broadens absorption bands. To appreciate this, we need to dig a little deeper. The O─H stretch in alcohols and carboxylic acids at ~3400 cm−1 is broadened by hydrogen bonding.
3400 cm−1 • 3.00E10 cm s-1 = 1.0E14 Hz = ν, the frequency at which O─H vibrates
The inverse of the frequency is the amount of time it takes to stretch and contract. Think about this for a bit. The units are right, inverting 1 /s give seconds, but doesn’t this make sense from an intuitive perspective? If you do something 10 times a minute, then each thing takes one tenth of a minute. So one of these vibrations takes (1.0E14 Hz)−1 = 1.0E−14 s. The limiting frequency at which diffusion takes out one molecule in a cluster of molecules, and puts in another in a different arrangement is about 1E9 Hz, so the lifetime of any molecular cluster, ~1E−9 s, is much longer than it takes the IR spectrometer to register a frequency in a molecule by a factor of about 100,000. The camera flashes before anyone says cheese, before anyone can compose themselves. The picture is pretty candid: Everyone is doing something different and nobody is posing. If IR were slow relative to diffusion phenomena the bands would get narrow; the wavenumbers would reflect a weighted averages of interchanging states.
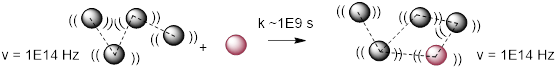
The rate constant to interconvert hydrogen bound states is much slower than the molecular vibrations. The IR ‘sees’ many states instead of an average state for any molecule.
Remember that C─H does not engage in strong molecular interactions, but O─H does. Furthermore, many atomic arrangements preserve RO─H---OHR hydrogen bonds. For example, in bond angle alone the HO—H hydrogen bond angle varies between 180° and perhaps 110°, the energy as the bond angle changes tends not to vary that much. Also, there can be more than one hydrogen bond to a hydrogen bond acceptor: H−−OH−−H. These effects make the IR wavenumber register at lower values than the unsolvated RO─H stretch. For this reason, functional groups that we label as ■ protic tend to have broad features in the IR spectrum.
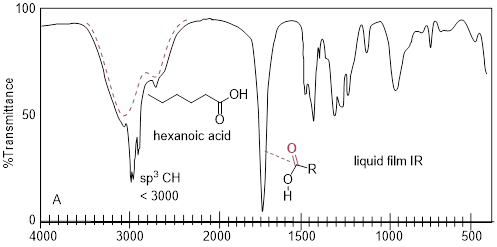
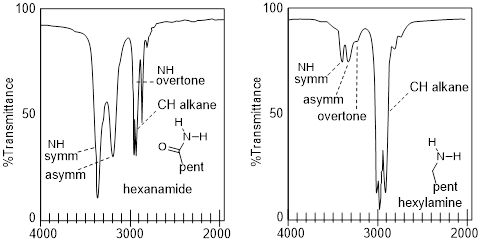
These band broadening effects can be seen in the liquid film IR spectrum of hexanoic acid above. The alkane C−H stretching signature is riding on the broad O−H stretching features (red dashed line). Many structural states contribute to the continuum of multiple frequencies in the O−H stretch region. Alkanoic acids can form ■ dimers (two molecules connected by two hydrogen bonds). The entire feature (broad band + shoulder band at lower frequency) has been attributed to the carboxylic acid dimer.
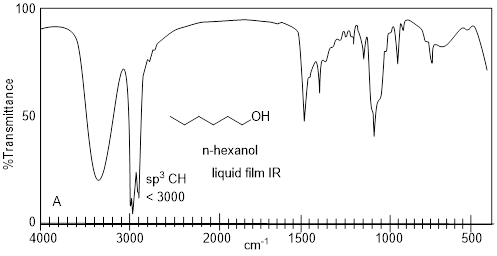
Let us consider the changes to the IR by making a small functional group change from one protic group to another, namely carboxylic acid to alcohol. In stark contrast to hexanoic acid, n-hexanol does not show the complex OH stretching bands, instead showing only one smooth broad feature in the 3000-3500 cm−1 region. In the spectrum below, n-hexanol loses the carbonyl signature at 1711 cm−1 of hexanoic acid while preserving the other features in the IR spectrum of hexanoic acid.
4.3.6 IR Spectra: Coupled Frequencies
Structural features that produce close stretching frequencies and are mechanistically related tend to couple. If multiple coupled stretches are occurring in the molecule, the spectrum can be complicated. Below compare the spectra of N-methylaniline with one N─H bond to that of p-toluidine which has two N─H bonds. N-methylaniline does not have coupling and we see that there is the typical single peak for the one N-H bone. However, there are two ways the N─H bond can stretch and change the dipole, 1) symmetrically (both at the same time), and 2) asymmetrically (one contracts while the other stretches). Even though we have two N−H bonds of the same energy, we get three bands and neither of the two addition bands are due to one of these N−H stretches acting independently. The symmetrical mode is at higher energy (see below); furthermore, the two modes interact in a manner similar to the way plucking a guitar string produces an overtone frequency, a more complex vibration.

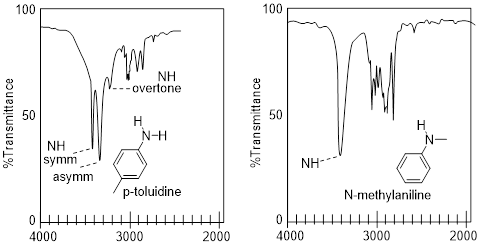
Another aspect of the coupling phenomenon is its directional nature. Amines tend to have weaker coupled frequencies than amides or the aniline in the figure above. The amine in the figure below at right is sp3 hybridized at the N atom and tetrahedral, whereas the anilines, and amides are sp2 hybridized at N, so the NH bonds lie in the same plane.
4.3.7 IR Spectra: Functional Group Identification
You can the following correlations to assign bands in the IR spectrum, and to help identify unknowns using IR spectral data. Be careful. Spectral features can ride under others, and complications due to coupled motions can arise. Features can be broadened by molecular interaction. Focus on the wavenumber of the band in the spectrum to correlate the functional group and think about molecular interactions and whether the appearance of the band makes sense.
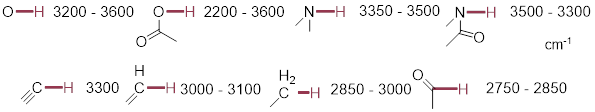
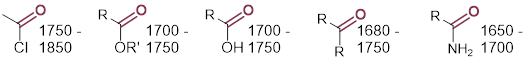
![]()
However, committing these to memory to use them is a misuse of neuronal space. There is much more value in utilizing PPs of spectra in order to learn functional group identification.
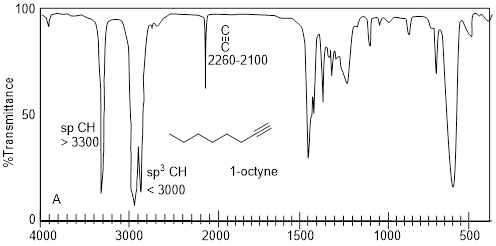
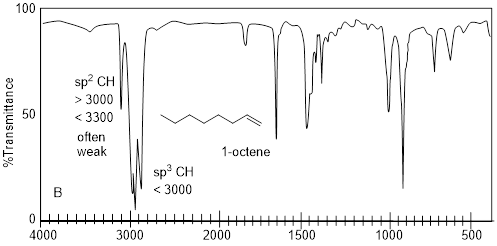
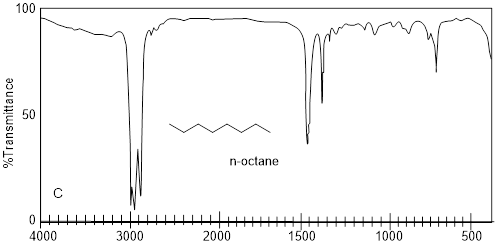
The spectra above are in % transmission mode, and this way of presenting IR spectra is most common when the method is used for characterization and the Beer-Lambert quantitative aspects of the intensity axis are not required. The transmission does not vary linearly with concentration. ■ Absorption mode usually has the features in the IR spectrum originating from a near zero baseline instead of a baseline of ~100%. The way the two modes relate with the following math.
![]()
Imagine having three bottles of translucent, clear, colorless liquids that do not dissolve in water. Let’s say that we know the molecules in each have 8 C atoms. Simply putting a drop on a small polished NaCl plate, putting another plate on top of the drop and putting the sample in the IR spectrophotometer generates the spectra above. Characteristic absorptions for sp-hybridized C-H bond stretches are at 3,300 cm−1 or greater. The only spectrum that has a feature that high in wavenumber is spectrum A. The signal at ~2200 cm−1 corroborates the presence of C≡C, because this value is characteristic of the CC triple bond stretch. In spectrum B, the weak signal at 3079 cm−1 indicates sp2-hybridized C-H bond stretches but beyond that there might not be much else in spectrum B with enough diagnostic power in which to put much faith. The sharp peak at 1642 cm−1 is the C=C bond stretch, and it corroborates the identification of the sp2-hybridized C-H bond stretch. More information may come from spectrum C by taking note of what is missing. In any case the spectra above are diagnostic of alkanes, alkenes and alkynes.
Weaker peaks at ~1400 cm−1 and below are termed the fingerprint region. This region is used to diagnose structural components to a lesser extent because it usually contains a very complicated series of absorptions. As no two fingerprints are identical, no two compounds’ fingerprint regions are identical unless you are examining two IR spectra of the same material.
This section provided you with a sensible series of approximations regarding where to find features on the IR spectrum wavenumber axis. Working problems will familiarize you further with IR spectroscopy.
Exercise 4.3.1 How might IR spectroscopy be used to analyze the reaction below?

Exercise 4.3.2 An unknown compound with molecular formula C3H8O shows a strong and broad signal in the IR spectrum at 3350 cm-1? Deduce the structure of the unknown compound. Hint: There might be more than one correct isomer.
Exercise 4.3.3 Which of the following structures is most consistent with this IR Spectrum?
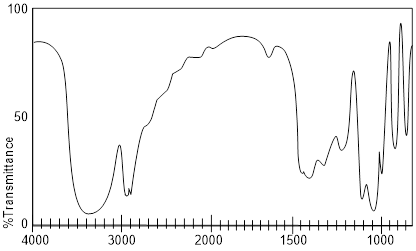
![]()
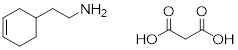
4.4 ISOMERS
(Ashley Jolly Steelman, 2019)
Isomers are molecules with identical molecular formulas, but differences in their overall structure. There are two major classifications of isomers, constitutional isomers and stereoisomers. We have previously discussed the concept of constitutional isomers - molecules that have the same molecular formula but differ in the way the atoms are connected (i.e. butane and isobutane, below right). In the next sections, we focus on stereoisomers. Stereoisomers are molecules that have the same molecular formula, the same ■ connectivity but differ in spatial arrangement (i.e. trans-2-butene and cis-2-butene, below left).
4.4.1 Stereoisomers / Enantiomers
In the upcoming chapters, we will examine the reactivity of several types of functional groups and realize that many of these organic reactions produce stereoisomers as products. It is important to recognize the difference between products when more than one is obtained. In many pharmaceuticals, slight differences in 3D spatial arrangement can make an enormous difference between a targeted treatment and an undesired side effect. The example below exemplifies the importance of recognizing stereoisomers. The two drugs have the same molecular formula, the same connectivity, but differ in the spatial arrangement of two carbon atoms and an oxygen atom. These two molecules are mirror images of each other; they are enantiomers. This small variance in structure makes all the difference when these two molecules are consumed. If a pharmacist switched these two molecules by mistake, it could be lethal.
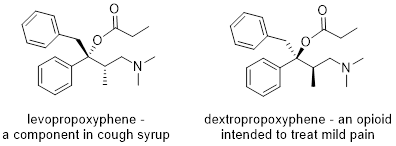
To communicate about stereoisomers like Levopropoxyphene and Dextropropoxyphene we need to understand the meaning of wedge and dash notation. Wedges and dashes represent 3D structures on paper. Any solid line represents bonds approximately in the plane of the page, a wedged line represents a bond coming out of the page, and a dashed line represents a bond extending back behind the page.
If we make a model of 2-iodo-2-chlorobutane, we can see that the four C atoms can be in the plane of the page, the Cl atom (green) is protruding back into the page, and the I atom (purple) coming out of the page. To draw this on paper, we use wedge and dash notation to show stereochemistry at carbon atom 2. We will see in the next section that atoms bound to four different groups often produce stereoisomers.
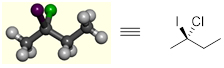
To identify stereoisomers, we
must first be able to identify a chiral molecule. A chiral molecule is
one that is NOT identical to its mirror image (this can result when a carbon atom is bonded to four unique groups).
However, ■ chirality is a property of objects,
not only molecules—or better said, molecules can be chiral because they are
also objects. For example, if we include your internal organs, and the way you
comb your hair, you are a chiral object. If you take your image out of the
mirror and place one on top of yourself you would see small differences like
the direction in which the hair is combed, zits and scars. We use the term non-superimposable
to describe mirror images of molecules that do not match atom-for-atom when we try to put them in the
same space. If the mirror image were identical to the actual object, we would
call the molecule achiral, meaning
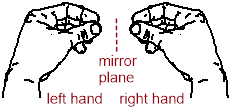
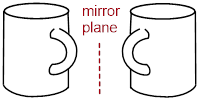
that it is superimposable on (identical to) its mirror image. Below, hands
demonstrate an enantiomeric pair of chiral objects, and a coffee mug
demonstrates an achiral object (an object that is identical to its mirror
image).
Note:
Visualizing mirror images of molecules
and manipulating them in 3D space is difficult. We highly recommended that you
use handheld models as visual aids.
4.4.2 Meso Compounds: Those that Posses an Internal Mirror of Symmetry
Notice above, that the coffee mug has an internal mirror plane, but the hand does not. When we try to spatially divide the fingers and the rest of the hand, we get the palm on one side of the plane and the back of the hand on the other side of the plane. The coffee mug has two halves on either side of the internal mirror. These halves are mirror images of each other, and they are superimposable. The internal mirror, or more commonly, ■ reflection plane, is an element of symmetry. If you can find it in a molecule, or any other object, it is achiral.
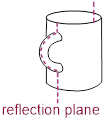

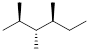
Atoms that have three or more different groups attached in a non-planar geometry are called ■ stereogenic atoms. You will see these referred to as stereo centers, chiral centers, or chirality centers, but realize that people are talking about the same thing. Examine trans- and cis-1,2-dimethylcyclohexane. These molecules have two chiral centers (labeled with asterisks) but the trans- molecule is chiral and the cis- molecule is achiral.
![]()
![]()
Cis-1,2-dimethylcyclohexane has an internal plane of symmetry. If you attempted to draw its mirror image you would find that the two images are superimposable with one another and are therefore the same molecule. A ■ meso molecule has a reflection plane making it achiral.
Look at the diol at left below. Its mirror image appears on its right, and at first, you might think these molecules look like enantiomers, but they are identical to one another. The diol can be arranged in a conformation with a reflection plane, red dashed line (right). Even though this conformation is high-energy, if this can be done, the molecule is achiral.

Meso compounds are achiral because one side of the molecule is the mirror image of the other. Each side of the molecule has opposite stereochemistry; the optical characteristics of each side of the mirror plane cancel each other. Another example is below.
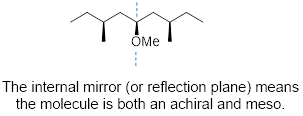
Exercise 4.4.1 Which of the following molecules can have an enantiomer?
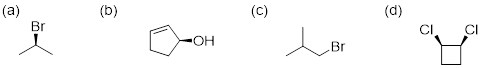
Exercise 4.4.2 Which of the following structures are meso compounds?
4.5 CHIRALITY AND NATURAL PRODUCTS
(Timothy Soderberg, Organic Chemistry with a Biological
Emphasis I, 2016. ( [ … ]
indicates deletion of Soderberg text.) (Additions and editions are mark with [
].
Consider the cartoon molecule A, below: […] with [stereogenic carbon atom C].
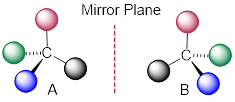
The mirror image of A, which we will call B, is drawn on the right side of the figure, and an imaginary mirror is in the middle. Notice that every point on A lines up through the mirror with the same point on B: in other words, if A looked in the mirror, it would see B looking back.
Now, if we flip compound A over and try to superimpose it point for point on compound B, we find that we cannot do it: if we superimpose any two colored balls, then the other two are misaligned.
A is not superimposable on its mirror image (B), thus by definition A is a chiral molecule. It follows that B also is not superimposable on its mirror image (A), and thus it is also a chiral molecule. Also notice in the figure below (and convince yourself with models) that neither A nor B has an internal plane of symmetry.
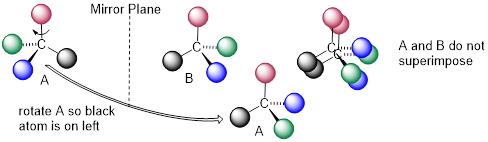
A and B are stereoisomers: molecules with the same molecular formula and the same bonding arrangement, but a different arrangement of atoms in space. There are two types of stereoisomers: enantiomers and diastereomers. Enantiomers are pairs of stereoisomers which are mirror images of each other: thus, A and B are enantiomers. It should be self-evident that a chiral molecule will always have one (and only one) enantiomer: enantiomers come in pairs. Enantiomers have identical physical properties (melting point, boiling point, density, and so on). However, enantiomers do differ in how they interact with polarized light (we will learn more about this soon) and they may also interact in very different ways with other chiral molecules - proteins, for example.
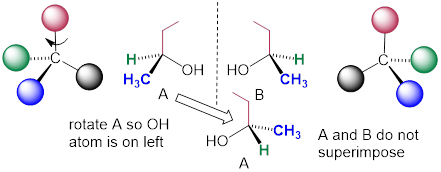
Consider 2-butanol, drawn in two dimensions below.
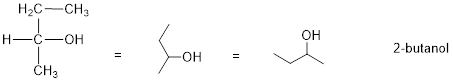
Carbon #2 is a chiral center: it is sp3-hybridized and tetrahedral (even though it is not drawn that way above), and the four things attached to it are different: a hydrogen, a methyl (-CH3) group, an ethyl (-CH2CH3) group, and a hydroxyl (OH) group. Let's draw the bonding at C2 in three dimensions, and call this structure A. We will also draw the mirror image of A, and call this structure B. When we try to superimpose A onto B, we find that we cannot do it. A and B are both chiral molecules, and they are enantiomers of each other.
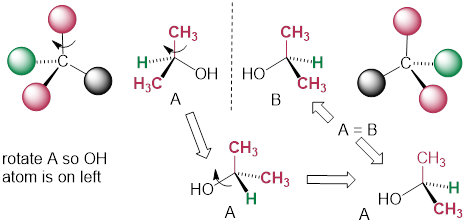
2-propanol, unlike 2-butanol, is not a chiral molecule. Carbon #2 is bonded to two identical substituents (methyl groups), and so it is not a chiral center. 2-propanol is achiral. Notice that 2-propanol is superimposable on its own mirror image. [ Notice also that 2-propanol has an internal mirror image; therefore, it cannot be chiral. ]
[ Below ] are more examples of chiral biomolecules, each one shown as a pair of enantiomers, with chiral centers marked by [ asterisks ].
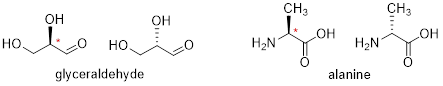

Here are some examples of achiral biomolecules - convince yourself that none of them contains a chiral center [ and that all of them have reflection planes ]:
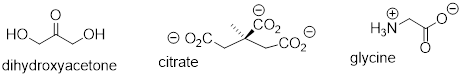

When looking for chiral centers, it is important to recognize that the question of whether or not the dashed/solid wedge drawing convention used is irrelevant. Chiral molecules are sometimes drawn without using wedges (although obviously this means that stereochemical information is being omitted). Conversely, wedges may be used on carbons that are not chiral centers – look, for example, at the drawings of glycine and citrate in the figure above.
[ (Ashley Jolly Steelman, 2019) Let’s try to identify chiral centers.
Example 4.5.1
Identify all chiral centers (using asterisks) in the following compound.
Solution
When locating chiral centers, we can ignore –CH2 and –CH3 groups because these groups already have at least two of the same atoms attached (multiple hydrogens). We should have located two carbons that we can classify as a chiral centers.
 ]
]
[ … ]
You may also have wondered about amines: shouldn't we consider a secondary or tertiary amine to be a chiral center, as they are tetrahedral and attached to four different substituents, if the lone-pair electrons are counted as a 'substituent'? Put another way, isn't an amine non-superimposable on its mirror image?
The answer: yes, it is, in the static picture, but, in reality, the nitrogen atom in an amine rapidly and reversibly inverts, or turns inside out, at room temperature.

[ (Arthur Cammers, 2019) Inversion was discussed in carbanions in the context of the improper dihedral angle in Chapter 2. At this point we are aware that molecules around equilibrium atomic positions, and we also know that the equilibrium atom position for the amine is a tetrahedral geometry because the lone pair and the σ bonds are better stabilized by orbitals with some s character at the N atom. To invert the N atom, the three groups attached to the N atom must go through a transition in which they lie in the same plane. This requires that the σ bonding be hybridized sp2 at the N atom and the lone pair be in a pure non-hybridized p orbital. The energy barrier to inversion of phosphines, :PR3, is high enough such that phosphines are chiral at room temperature.
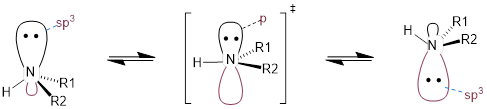
Dynamic equilibrium is also the way that cis-1,2-dimethylcyclohexane is achiral. We will discuss the conformations of cyclohexane soon but let’s just leave it here that cis-1,2-dimethylcyclohexane switches quickly between chiral conformations and is thus dynamically achiral.
 ]
]
4.5.1 R/S Configuration
[(Ashley Jolly
Steelman, 2019) Even though enantiomers
bear the same physical properties, they are NOT identical molecules, so how do
we give different names to them?
![]()
From what we know about
nomenclature currently, we should come up with the same name for both
molecules, 2‑chlorobutane. However, we need a way to name each
enantiomer, so we use the ■ Cahn-Ingold-Prelog system to designate each molecule as either R
(rectus meaning right) or S (sinister meaning left). Enantiomers will
have the exact same IUPAC names but opposite configurations with one designated
as S and other designated as R.
The Cahn-Ingold-Prelog system
rules:
1.
Using atomic numbers, prioritize the 4 groups attached to the
chirality center with #1 being highest priority (highest atomic number) and #4
being the lowest priority (lowest atomic number).
2.
Arrange the molecule in space so the lowest priority group
points away from you.
3.
Count the group priorities 1…2…3 (leave out 4) to determine
whether the order progresses in a clockwise or counterclockwise direction.
4.
Clockwise = R configuration
and Counterclockwise = S configuration.
(end of Ashley Steelman’s
contribution to this section)]
We’ll use the 3-carbon sugar glyceraldehyde as our first example. The first thing that we must do is to assign a priority to each of the four substituents bound to the chiral center. We first look at the atoms that are directly bonded to the chiral center: these are H, O (in the hydroxyl), C (in the aldehyde), and C (in the CH2OH group).
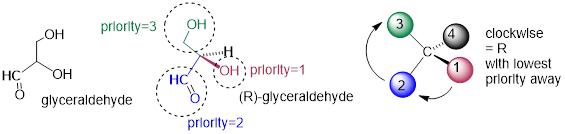
Assigning R / S configuration to glyceraldehyde
Two priorities are easy: hydrogen, with an atomic number of 1, is the lowest (#4) priority, and the hydroxyl oxygen, with atomic number 8, is priority #1. Carbon has an atomic number of 6. Which of the two ‘C’ groups is priority #2, the aldehyde or the CH2OH? To determine this, we move one more bond away from the chiral center: for the aldehyde we have a double bond to an oxygen, while on the CH2OH group we have a single bond to an oxygen. If the atom is the same, double bonds have a higher priority than single bonds. Therefore, the aldehyde group is assigned #2 priority and the CH2OH group the #3 priority.
With our priorities assigned, we look next at the #4 priority group (the hydrogen) and see that it is pointed back away from us, into the plane of the page […]. Then, we trace a circle defined by the #1, #2, and #3 priority groups, in increasing order. The circle is clockwise, which by step 4 tells us that this carbon has the ‘R’ configuration, and that this molecule is (R)-glyceraldehyde. Its enantiomer, by definition, must be (S)-glyceraldehyde.
The drug thalidomide is an interesting - but tragic - case study in the importance of stereochemistry in drug design. First manufactured by a German drug company and prescribed widely in Europe and Australia in the late 1950's as a sedative and remedy for morning sickness in pregnant women, thalidomide was soon implicated as the cause of devastating birth defects in babies born to women who had taken it. Thalidomide contains a chiral center, and thus exists in two enantiomeric forms. It was marketed as a racemic mixture: in other words, a 1:1 ratio of both enantiomers.
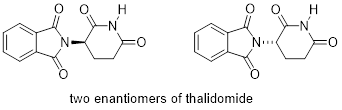
Let’s try to determine the stereochemical configuration of the enantiomer on the left. Of the four bonds to the chiral center, the #4 priority is hydrogen. The nitrogen group is #1, the carbonyl side of the ring is #2, and the –CH2 side of the ring is #3.
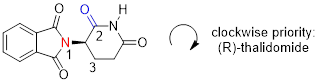
The hydrogen is shown pointing away from us, and the prioritized substituents trace a clockwise circle: this is the R enantiomer of thalidomide. The other enantiomer, of course, must have the S configuration.
Although scientists are still unsure today how thalidomide works, experimental evidence suggests that it was the R enantiomer that had the desired medical effects, while the S enantiomer caused the birth defects. Even with this knowledge, however, pure (R)- thalidomide is not safe, because enzymes in the body rapidly convert between the two enantiomers […].
As a historical note, thalidomide was never approved for use in the United States. This was thanks in large part to the efforts of Dr. Frances Kelsey, a Food and Drug officer who, at peril to her career, blocked its approval due to her concerns about the lack of adequate safety studies, particularly with regard to the drug's ability to enter the bloodstream of a developing fetus. Unfortunately, though, at that time clinical trials for new drugs involved widespread and unregulated distribution to doctors and their patients across the country, so families in the U.S. were not spared from the damage caused.
Exercise 4.5.1 Identify the configuration as R or S of each chral atom in the following compounds.

4.6 Chiral Compounds that Lack a Chiral Center
(Arthur Cammers, 2019)
At this point we have
established that chirality is not a property of atoms, but of objects. It is no
surprise then that there are ways to arrange atoms in molecules that produce
chirality without using stereogenic atoms. Given what you know about molecular
geometry and chirality, you should now be able to recognize that ■ cumulated dienes (see also ■ allene) is a
structural features that can give rise to chirality.
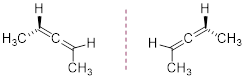
The two molecules above are
(P)-2,3-pentadiene or (R)-… and (M)-2,3-pentadiene or (S)-... The rules for R /
S nomenclature of these chiral molecules can be found in the allene link above.
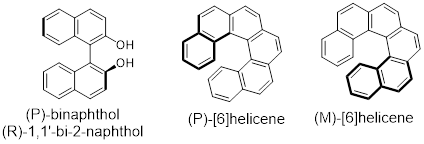
However, P / M nomenclature can be applied more broadly to ■ axial chirality (object-based
molecular chirality). More examples below can be found in ■ binaphthol and
in a family of molecules called ■ helicenes in which
steric interactions in the molecule extrude the structure out of planarity.
In the molecules below, the bold lines are closer to the reader. Notice that if you put the pinky edge of your right hand down on (P)-[6]helicene and you follow the direction of your fingers around the ramp of the helicene, your hand comes up toward you in the direction your thumb points. This is the ■ right hand rule for naming helices and screws; it distinguishes P from M. You need to use your left hand for the ramp of the helix to push your thumb toward you with the M enantiomer.
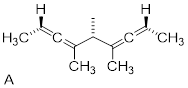
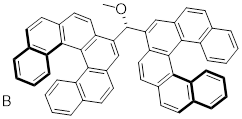
Exercise 4.6.1 Test your understanding. Does structure A below have a stereogenic atom? Is A chiral? Does structure B have a stereogenic atom? Is B chiral?
 4.7 OTICAL ACTIVITY
4.7 OTICAL ACTIVITY
(Arthur Cammers, 2019) Image: Sunlight and shadow through a pair of 3D movie eyeglasses. These plastic lenses are a layered combination of circularly and linearly polarized light filters. (Arthur Cammers, 2019)
We can make two statements regarding enantiomers: 1) Enantiomers have identical physical properties. This is a universal truth—and there are not that many truisms available. A liquid sample of one enantiomer (neat or in solution) can rotate the plane of polarized light. 2) The other enantiomer, under the same conditions, rotates same frequency polarized light in the opposite direction by the same amount. However, if statement 1 is true we should not be able to find a way to differentiate the two enantiomers, even with light. To tell them apart experimentally they must have different physicochemical properties. We have an answer to this question, and it will assist our conceptualization of everything in the next few sections.
The EM field oscillates in a plane and propagates linearly. Regular non-polarized light is the addition of light rays oscillating in all possible planes. When light passes through a polarizing lens however the other rays of light that are not parallel to the filter are left behind. The filter passes only the light that is in the plane of the filter.

The observer sees plane polarized light which is an oscillating electromagnetic field in the plane of the polarizer. Plane polarized light is the sum of two vectors that ‘spiral’ separately through the translucent sample. If we were to measure the direction of magnitude of these two electric field vectors the observer above perceives the image below with time as light exits the sample. Below we are observing the electric field vector of polarized light coming straight at us through an achiral sample and it is the sum of two vectors.
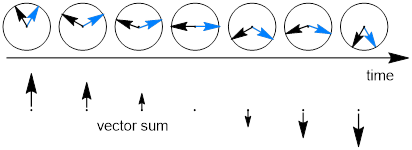
You may have heard that the velocity of light is a constant, but this statement only refers to the vacuum of space in which there is very little matter. Light is a disturbance in the electromagnetic field, a property of space. As you know the EM field interacts strongly with fermionic systems … like molecules composed of fermions (electrons and protons in nuclei). The index of refraction, n, of some substance x: nx = c/vx where vx is the velocity of light in x.
As one of these circular vectors passes through space (black or red in figure above) it draws a spiral. Helices or spirals are chiral; the mirror image of the helix is not identical to the helix; they are enantiomeric. As such, they have identical velocities.
However, when the sample contains only one enantiomer, perhaps an R molecule dissolved in an achiral solvent, the interaction between the P vector and R molecule is now different than the interaction between the M vector and the R molecule. These two couples are reflected across the mirror plane. Are no longer mirror images like the two vectors without the R molecule were mirror images.
P vector + R molecule | no | M vector + R molecule
P vector | yes | M vector
The interaction with the R molecule has broken the symmetry and now there is no reason why the velocities of both light spirals should be equal. One light vector will propagate faster than the other. Thus, the polarized light escaping the surface of the sample container now looks like the phenomenon below, in which the original plane polarized light has been tilted by some angle because one vector was slowed down relative to the other. In the image below the M vector is faster than the P vector in the chiral medium. This theory of interaction tells us that the extent of tilting of the plane of polarized light should depend directly on the path length of the sample container and the concentration of the enantiomer, and that is exactly what is observed.
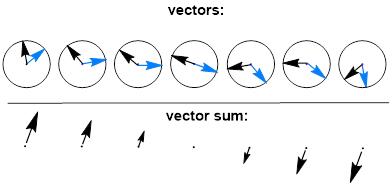
Since the light and the molecule have chiral elements that can be considered independent or a coupled entity, we call this mix and match relationship { P vector + R molecule } and { M vector + R molecule } a diastereomeric relationship.
Take some time to process the following, if we analyze the S molecule in the same polarized light, we should have a tilt in exactly the opposite angle by the same magnitude, right? This is because the { P vector + R molecule } is enantiomeric to the { M vector + S molecule }. The velocity of the light vectors should be identical. Likewise the { M vector + R molecule } is enantiomeric to the { P vector + S molecule }. These two pairs should have identical physical properties in all respects due to the truism that enantiomers are not distinguishable. Thus, the enantiomer must rotate polarized light by the same amount, but in the opposite direction.
Specific rotation [α] defines enantiomers uniquely, [α]D = observed rotation of the plane of polarized light for 1g /mL through 1 dm, defined for the yellow light emitted by the excitation of a ■ sodium lamp (589 nm). The D in [α]D is the sodium D line emission. The relationships between [α]D and pathlength and concentration are linear, so we can calculate the [α]D of any chiral substance using any pathlength and any concentration.
[α]D /(1 dm)(1 g/mL) = α /(c)( L )
This is just a proportion and is simplified into the following equation
[α]D = α /c L
in which α is the angle of rotation of the plane polarized light that we measure, and L and c are the pathlengths and concentrations used to measure it, in g mL-1 and dm respectively.
Example 4.7.1
Calculate [α]D for L(−)-fenchone with observed rotation −6.31° at 0.25 g /mL and 5 cm pathlength.
Solution
−6.31 / 0.25 g / 0.5 dm = −50.5
In summary, enantiomeric relationships and enantiomers themselves have identical physicochemical properties. Diastereomeric relationships and diastereomers (discussed in section 4.8) themselves have different physicochemical properties.
4.7.1 Optical Purity
When a mixture of enantiomers reaches its maximum value of α as a function of the ratio of one enantiomer to the other we call this mixture optically pure. This means that there is only one enantiomer in the mix. The ■ racemic mixture does not rotate the plane of polarized light because one enantiomer produces the opposite effect as the other enantiomer. If there is a percent excess of one enantiomer, the plane of polarized light will rotate. The racemic mixture dilutes the ability of the plane of polarized light to rotate and this dilution is a linear function of the ■ enantiomeric excess (%ee). Some fraction of any mixture of enantiomers will be pure and this will be the concentration of one enantiomer minus the concentration of the opposite enantiomer divided by the total.
%ee = ([R] − [S]) / ([R] + [S]) • 100%
Example 4.7.2
Calculate the % ee of 1 : 4 mixture of S : R enantiomers.
Solution
( 4 – 1 ) / (4 + 1) •100% = 60% ee in the R enantiomer
Example 4.7.3
For a mixture of enantiomers of mandelic acid, the [α]D is determined to be −67.0°. [α]D = +153±5° in H2O for L-(+)-mandelic acid. What is the ratio of L-(+)-mandelic acid : D-(−)-mandelic acid?
Solution
−67 / −153° • 100% = 43.8% ee D-(−)-mandelic acid
0.438 = (X−1) / (X+1)
0.438X + 0.438 = X −1
0.562 X = 1.438
X = 2.56
L-(+)-mandelic acid : D-(−)-mandelic acid = 1 : 2.56
4.8 MULTIPLE CHIRAL ELEMENTS / DIASTEREOMERS
(Timothy Soderberg, Organic Chemistry with a Biological Emphasis I,
2016.)
Next, we turn our attention to [ compounds ] which have multiple chiral centers. We'll start with some stereoisomeric four-carbon sugars with two chiral centers.
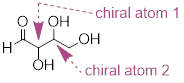
To avoid confusion, we will simply refer to the different stereoisomers by capital letters.
Look first at compound A, below. Both chiral centers have the R configuration (you should confirm this for yourself!). The mirror image of Compound A is compound B, which has the S configuration at both chiral centers. If we were to pick up compound A, flip it over and put it next to compound B, we would see that they are not superimposable (again, confirm this for yourself with your models). A and B are nonsuperimposable mirror images: in other words, enantiomers.
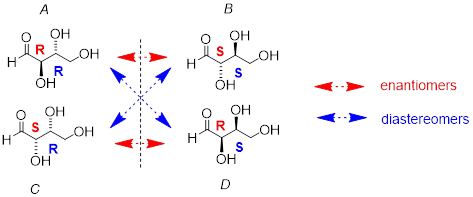
This diagram should remind you of the description of the phenomenon of optical rotation.
Now, look at compound C, in which the configuration is S at chiral center 1 and R at chiral center 2. Compounds A and C are stereoisomers: they have the same molecular formula and the same bond connectivity, but a different arrangement of atoms in space (recall that this is the definition of the term 'stereoisomer). However, they are not mirror images of each other (confirm this with your models!), and so they are not enantiomers. By definition, they are diastereomers of each other.
Notice that compounds C and B also have a diastereomeric relationship, by the same definition.
So, compounds A and B are a pair of enantiomers, and compound C is a diastereomer of both of them. Does compound C have its own enantiomer? Compound D is the mirror image of compound C, and the two are not superimposable. Therefore, C and D are a pair of enantiomers. Compound D is also a diastereomer of compounds A and B.
This can also seem very confusing at first, but there some simple shortcuts to analyzing stereoisomers:
Here's another way of looking at the four stereoisomers, where one chiral center is associated with red and the other blue. Pairs of enantiomers are stacked together.
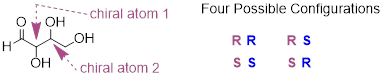
We know, using the shortcut above, that the enantiomer of RR must be SS - both chiral centers are different. We also know that RS and SR are diastereomers of RR, because in each case one - but not both - chiral centers are different.
Now, let's extend our analysis to a sugar molecule with three chiral centers. Going through all the possible combinations, we come up with eight total stereoisomers - four pairs of enantiomers.
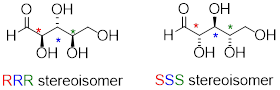
Now, using the above drawing as our model, drawing any other stereoisomer is easy. If we want to draw the enantiomer of RRR, we don't need to try to visualize the mirror image, we just start with the RRR structure and invert the configuration at every chiral center to get SSS.
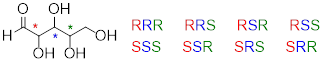
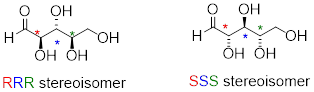
Try making models of RRR and SSS and confirm that they are in fact nonsuperimposable mirror images of each other.
There are six diastereomers of RRR. To draw one of them, we just invert the configuration of at least one, but not all three, of the chiral centers. Let's invert the configuration at chiral center 1 and 2, but leave chiral center 3 unchanged. This gives us the SSR configuration.
One more definition at this point: diastereomers which differ at only a single chiral center are called epimers. For example, RRR and SRR are epimers:
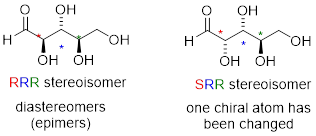
The RRR and SSR stereoisomers shown earlier are diastereomers, but they are not epimers because they differ at two of the three chiral centers.
The epimer term is useful because in biochemical pathways, compounds with multiple chiral centers are isomerized at one specific center by enzymes known as epimerases. Two examples of epimerase-catalyzed reactions are below.
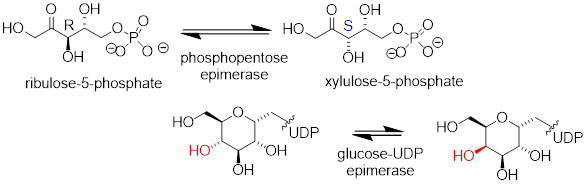
We know that enantiomers have identical physical properties and equal but opposite magnitude specific rotation. Diastereomers, in theory at least, have different physical properties – we stipulate ‘in theory’ because sometimes the physical properties of two or more diastereomers are so similar that it is very difficult to distinguish between them. In addition, the specific rotation values of diastereomers are unrelated – they could be the same sign or opposite signs, similar in magnitude or very dissimilar.
Now, let's compare the structures of the two sugars D-glucose and D-gulose, and try to determine their relationship.
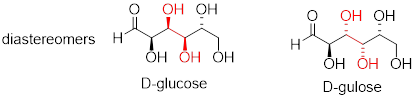
The two structures have the same molecular formula and the same connectivity. Therefore, they must be stereoisomers. They each have four chiral centers, and the configuration is different at two of these centers (at carbons #3 and #4). They are diastereomers.
Now, look at the structures of D-glucose and D-mannose.
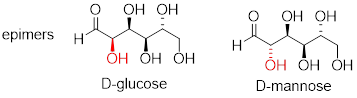
Here, everything is the same except for the configuration of the chiral center at carbon #2. The two sugars differ at only one of the four chiral centers, so again they are diastereomers, and more specifically they are epimers.
D-glucose and L-glucose are enantiomers, because they differ at all four chiral centers.
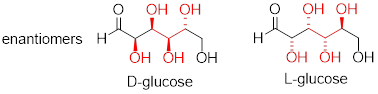
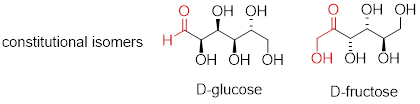
D-glucose is the enantiomer commonly found in nature. D-glucose and D-fructose are not stereoisomers, because they have different bonding connectivity: glucose has an aldehyde group, while fructose has a ketone. The two sugars do, however, have the same molecular formula, so by definition they are constitutional isomers.
[(Ashley Jolly Steelman, 2019
Example 4.8.1 Draw all possible stereoisomers of tartaric acid.
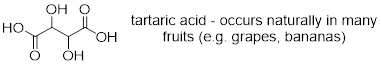
Solution
The compound has two chirality centers, so we would expect
there to be four possible stereoisomers (two pairs of enantiomers).
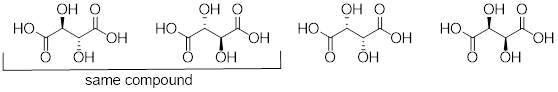
However, the first two molecules represent the same compound. They are meso compounds. In order to convince ourselves of this reality we need to recall that single bonds rotate freely.
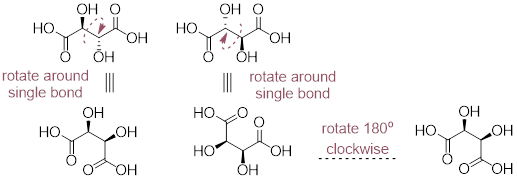
Tartaric acid is only comprised of three stereoisomers. If you drew all four of the stereoisomers above, then you would be incorrect since two of your molecules are identical.
(end of Ashley Steelman’s contribution to
this section)]
Exercise 4.8.1 Test your understanding. Draw a diastereomer for the following compounds. Hint: There might be more than one correct answer.

Exercise 4.8.2 For each of the following pairs of compounds, determine the relationship between the two compounds (constitutional isomers, identical, enantiomers, diastereomers).

4.9 RESOLUTION OF ENANTIOMERS
(Arthur Cammers, 2019)
Recall that enantiomers are physically indistinguishable in most tests like melting point, boiling point, solubility and IR spectroscopy. Therefore, how can we separate ■ racemic mixtures. If the two stereoisomers have the same physicochemical properties, there is no physicochemical property that we can use to resolve them. For example, enantiomers have identical boiling points so distillation will not work, and the list of frustration continues. Let us examine a couple tricks that we can use to get the job done.
4.9.1 Asymmetric Crystallization
Asymmetric crystallization or resolution by crystallization is known to occur in perhaps 10% of enantiomeric substances. To appreciate how a partially racemic solution can crystallize out one enantiomer spontaneously and leave the other in solution we need to baby step through what happens when substances crystallize. A crystal is a periodic arrangement of molecules in a solid matrix. It you take any linear path through a crystal at some point you see the same atoms in exactly the same places. To produce this ordered solid state two molecules must partially dissolve out of solution and interact with each other. In this process solvent molecule contacts are foregone for contacts between the solute. In a racemic mixture the bimolecular contacts are of two types.
(1) R•R or S•S or (2) S•R
R•R(aq) ─► R•R• R•R• R•R• R•R• R•R(s)
Most molecules prefer to crystallize in mode 2). However, some fraction prefer mode 1) and here is where we get the magic. R•R and S•S are enantiomers and thus have identical interactions with the solvent and with themselves. S•R versus either R•R or S•S are diastereomeric. Their solubilities, the magnitudes of their interactions with self and the kinetics of their interactions all differ.
In the case in which we have an excess of one enantiomer, we can purify it away from the other by crystallization because of one enantiomer being more concentrated than the other and it prefers the optically pure solid. Crystallization is autocatalytic: Once one solid is present, it brings the other solid out of solution faster. Therefore, if we have a small amount of optically pure material, we can introduce it into a racemic solution. If the homochiral solid state is preferred.
This is the way Louis Pasteur discovered chiral aspects of molecules by recognizing R from S solid crystals of ■ tartrate in old wine samples. Just like one can recognize one enantiomer molecule from the other on the page, one can in certain circumstances distinguish enantiomeric crystals. The ability to separate the pairs of enantiomers relied on a difference in physicochemical properties of diastereomeric interactions. All resolutions of racemic mixture rely on diastereomeric relationships.
4.9.2 Derivatization
The molecules of life are in general optically pure. An easy bond to make and break is the C−O bond of esters. I had a lab mate back in the day who would make an ester to feel better about himself after a series of failed experiments. (R)-(−)-α-methoxyphenylacetic acid is available from nature. Imagine having to separate a racemic mixture of (trans)-2-methyl-cyclohexan-1-ol.
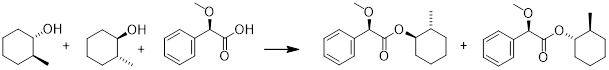
After the esterification process we have a mixture of diastereomers on the right side. These have different physicochemical properties and can be separated by a variety of methods.
There are oodles of techniques that fall under the category of derivatization. Racemic amines and optically pure organic acids react to make salt pairs. If one, the acid or the amine is available from a natural source in high optically purity they can be mixed to form the salt pair and preferentially crystallized from solution. They will have different solubilities because the salt pairs are diastereomers. Remember that amines are basic and acids are … well … acidic.
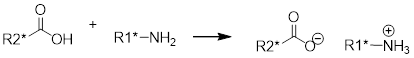
Examples: The methyl ester of naturally occurring valine in the potential resolution of chiral carboxylic acids.
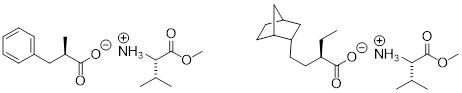
4.9.3 Chromatography
■ Chromatography is usually employed as an analytical technique. If you are unfamiliar with these techniques, you should click the link and read. Allowing an eluent to progress on a stationary phase can tell the experimenter what is present in solution, or if a reactant in a chemical process has been depleted to the point that the reaction should be stopped and the products isolated and purified. When the stationary phase possesses optically pure components preparative chromatography allows the separation of enantiomers because the retention times on the stationary phases is just another physicochemical property. The interactions of the R enantiomer with the S stationary phase is different than the interaction tween the S enantiomer.
4.9.4 Enzymatic Resolution
At this point we know that enzymes are catalysts and they are long, optically pure, protein chains that fold in functional conformations. For catalysis to occur, the substrate must first interact with the catalyst in a catalytic complex. This is followed by a series of low-energy intermediates that allow a low-energy pathway of the reaction to occur. Since the interaction between the enzyme and the R enantiomer is diastereomeric to the interaction with enzyme and the S enantiomer, whatever chemistry catalyzed by the enzyme happens faster with one enantiomer than the other. This is an example of kinetic resolution because the resolution is based on a kinetic pathway instead of intrinsic difference in the stabilities of ground state molecules.
There are oodles of enzyme that catalyze many reactions; however, I give an example below of the hydrolysis of a racemic ester catalyzed by candida lipase to yield optically pure alcohol.
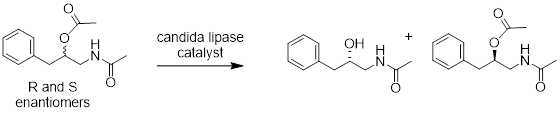
4.10 REVIEW OF STEREOISOMERS
(Timothy Soderberg, Organic Chemistry with a Biological
Emphasis I, 2016)
You should understand the relevant terms and concepts:
[A chiral object or molecule is not that same as its mirror image.
A chiral center is an atom bound to at least three different groups in a non-coplanar arrangement. Usually a chiral center, stereocenter, stereogenic atom, or chirality center (synonyms) is bound to four different groups. Atomic centers do not have to be C atoms.
Nomenclature: Chiral atom can be labeled R or S, these are included in the names.]
Stereoisomers have the same molecular formula and same connectivity, but a different orientation of atoms in space.
·
Enantiomers are stereoisomers which are mirror
images.
o
In
practice, the enantiomer of a compound is the one in which all chiral centers
are in the opposite configuration.
o
Every
chiral molecule has one and only one enantiomer.
o
Achiral
molecules are superimposable on their mirror image, and thus cannot have an
enantiomer.
o
Enantiomers
have equal but opposite specific rotations, but identical physical properties
otherwise.
·
Diastereomers are stereoisomers that are not
mirror images. They have different physical properties.
o
In
practice, a diastereomer of a chiral molecule with have at least one, but not
all chiral centers in the opposite configuration.
o
Alternatively,
two diastereomers may contain a stereogenic alkene with the opposite E/Z
configuration.
o
A
molecule has 2n - 2 diastereomers, where n is the number of chiral centers plus
stereogenic alkene groups. Meso compounds are an exception to this rule.
·
Epimers are diastereomers which differ at
only one chiral center.
·
A
racemic mixture is a 50:50 mixture
of two enantiomers.
·
A
meso compound has multiple chiral
centers but, because it has a plane of symmetry, is achiral.
CHAPTER 4 KEY FOR EXERCISES
(Susan Odom, Arthur Cammers and Ashley Steelman, 2019)
Exercise
4.2.1. 5,6-diethyl-4,7-dimethyldecane,
2-methyl-hex-3-ene (or 2-methyl-3-hexene)
Exercise
4.2.2. From left to
right: amide, alkyne, carboxylic acid
Exercise
4.2.3.
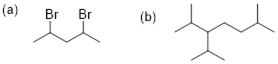
Exercise
4.2.4.
1-chloro-2-methylcyclohexane, 5-cyclobutylhexyne
Exercise
4.2.5.
fused bicyclic systems
Exercise
4.2.6.
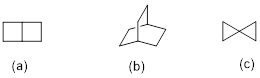
Exercise 4.2.7.
bicyclo[4.2.2]decane, spiro[2.4]heptane, bicyclo[4.3.0]nonane
Exercise 4.3.1. The IR
spectrum of our starting materials would show a broad signal around 3300 cm−1.
However, as our product started to form, we would see the signal around 3300 cm-1
diminish and a strong signal would appear around 1720 cm-1.
Exercise 4.3.2. Since we are given the molecular
formula, the first piece of information that we can deduce is the HDI
calculation (HDI = 0). This tells us that our molecule has to be completely
saturated with no double bonds, triple, bonds, or rings. From the IR information,
we should realize that there is an –OH functional group. There would be no way
to determine, with the information presented, which isomer of C3H8O
that we are looking at so either compound below is correct.
![]()
Exercise 4.3.3. The IR spectrum has a large broad
peak around 3350 cm-1 which is where we should find an –OH peak. We
can rule out all answers with a carboxylic acid functional group because we do
not see the carboxyl (C=O) peak that would show up around 1720 cm-1.
The correct answer is glycerol.
![]()
Exercise
4.4.1 (a) is achiral. (b)
![]() (c) is achiral. (d) is a meso compound so it
is also achiral.
(c) is achiral. (d) is a meso compound so it
is also achiral.
Exercise
4.4.2 C, and D are
meso compounds. (If D is giving you trouble, look at it this way: if you rotate
D along the C2–C3 sigma bond, you can see that one side is in fact the mirror
image of the other side). A is not a meso compound as it has no stereocenters.
B is not a meso compound; while it does have two stereocenters it does not have
an internal mirror plane. Its two opposing stereocenters have different
attachments.
Exercise
4.5.1 Identify the
configuration as R or S of each chiral atom in the following compounds.

Exercise
4.6.1 Test your understanding. Does structure A below have a stereogenic
atom? Is A chiral? Does structure
B have a stereogenic atom? Is B chiral?
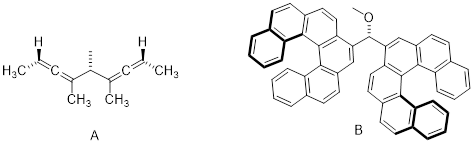
Answer: Does structure A have a stereogenic atom? Yes,
The C atom in the center is connected to
four different groups 1) M-allene, 2) methyl, 3) P-allene, and 4) H atom.
Is A chiral?
No because structure A has a reflection plane.
Answer: Does structure B have a stereogenic atom? No.
The chiral atom in B is connected to two P-helicenes.
Is B
chiral? Yes. B has no reflection plane.
Exercise 4.8.1 Diastereomer
- a chiral molecule with at least one, but not all chiral centers in the
opposite configuration. There are additional answers other than the ones
presented.
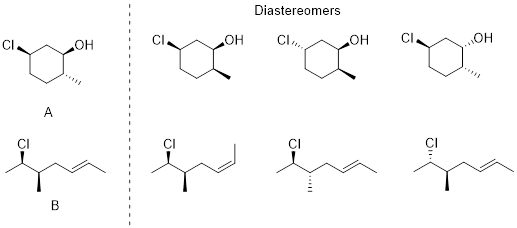
Exercise
4.8.2 a) Diastereomers b) Identical – if you deduce the IUPAC
name for each of these structures you will find that they are both (S)-2-
pentanol.
CHAPTER 4 PRACTICE PROBLEMS
PP 4-1 Determine the number of chiral centers in the molecule penicillin shown below. Note that stereochemical indicators (wedges, dashes) have been removed from the drawing of this structure.
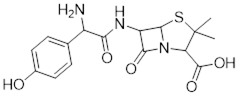
PP 4-2 Determine if the configuration is R or S for all chiral centers below.

PP 4-3 Draw the line
structures for molecules with the following names.
(a) (S)-2-chloro-3-heptene
(b) (1S,2R)-1-bromo-2-methylcyclopentane
(c)
spiro [5,2] octane
PP 4-4 How many stereoisomers are possible for the molecule shown below?
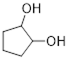
PP 4-5 For each of the following pairs of compounds, determine the relationship between the two compounds (constitutional isomers, identical, enantiomers, diastereomers).
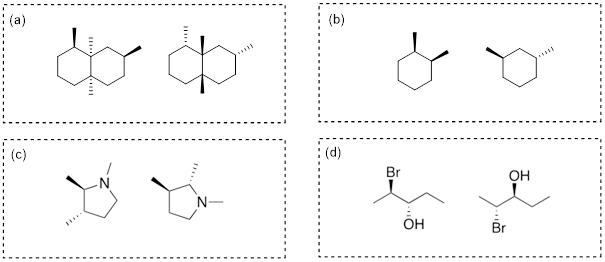
PP 4-6 Draw the enantiomer of each of the following compounds. If it is not possible to draw the enantiomer of any of the structures explain why.
PP 4-7 Draw the diastereomer of each of the following compounds. If it is not possible to draw the diastereomer of one of the structures explain why.
PP 4-8 Which of the
following compounds are meso compounds?
(a) (2R,3R)-dibromobutane
(b) (2R,3S)-dibromobutane
(c)
(2R,3S)-3-bromo-2-butanol
(d) (2R,3R)-3-bromo-2-butanol
PP 4-9 In the
following molecule, the atoms connected to platinum and platinum itself are in
the same plane. The metal is attached to four different substituents. Is the
molecule chiral? Why not?
PP 4-10 Is it theoretically possible to separate the pair of compounds below by distillation? Explain briefly.

PP 4-11 Compare the structures of cyclohexane and 2-methyl-2-pentene:
(a) What is the molecular formula for each compound?
(b) What is the HDI of each compound?
(c) Can IR spectroscopy be used to distinguish between these compounds? Explain.
|
PP 4-12 Which of the following bonds would show the strongest (sharpest) absorption in the IR spectrum? Provide a brief explanation for your choice. carbon-hydrogen oxygen-hydrogen nitrogen-hydrogen sulfur-hydrogen |
|
|
PP 4-13 Which structure below would give a peak at the highest (largest) wavenumber in an IR spectrum? Provide a brief explanation for your choice.

PP 4-14 Which of the following structures is consistent with this IR spectrum?
a)
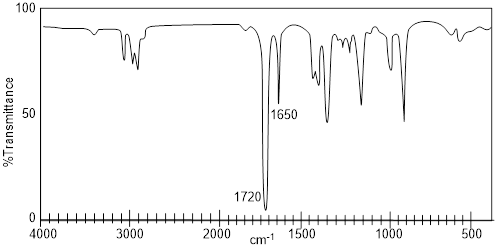

b)
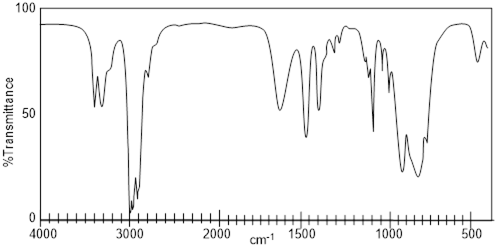

c)
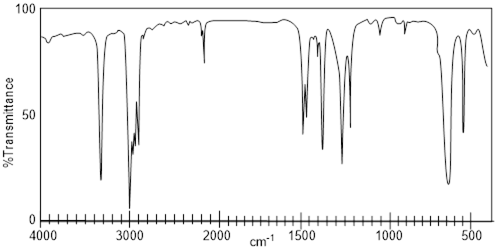

PP 4-15 How might IR spectroscopy be used to analyze each reaction below?
a) b)
![]()

PP 4-16 An unknown compound with molecular
formula C3H6O shows a strong signal in the IR spectrum at
1720 cm-1? Deduce the structure of the unknown compound.
PP 4-17 It
is possible for a molecule to be chiral even if it does not contain tetrahedral
carbon atoms. Of the two molecules below, one of them is chiral, and the other
is not.
(a) Draw the mirror image of each
molecule.
(b) For each pair, identify if the
mirror images are the identical or are enantiomers.
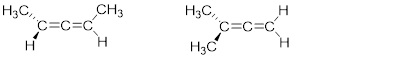
PP 4-18 Is the molecule below chiral? Does the molecule possess a
chiral atom?
CHAPTER 4 KEY FOR PRACTICE PROBLEMS
PP 4-1 Answer:
PP 4-2 Answer:

PP 4-3 Answer:
(a) (b) (c)
![]()
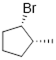
![]()
PP 4-4 Answer:If we attempt to draw each isomer and its mirror image, we will see that A and B are the same meso compound because they have an internal mirror plane that is shown on A. There are only 3 possible stereoisomers that can be drawn for this diol.
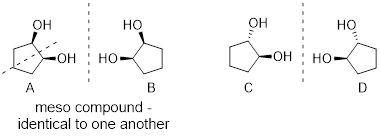
PP 4-5 Answer:
a)
Enantiomers
b)
Constitutional isomers
c)
Enantiomers
d)
Identical
PP 4-6 Answer:
PP 4-7 Answer:
PP 4-8 Answer: Recall that single bonds rotate. If you attempted to draw the enantiomer of compounds (b) you would find a plane of symmetry after the C2-C3 sigma bond has been rotated and therefore it is the only meso compounds. Compound (c) is very similar however since the two substituents are not identical, we no longer have a plain of symmetry.
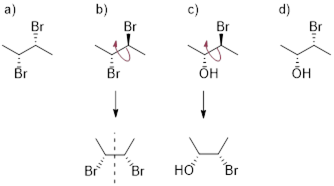
PP 4-9 Answer:
PP 4-10 Answer: Yes. The molecules are related as diastereomers and hence have different boiling points.
PP 4-11 Answer:
(a) C6H12 ![]()
(b) HDI = 1
(c) Yes, IR spectroscopy can be used to distinguish between these compounds. The IR spectrum for 2-methyl-2-pentene would have a signal for the sp3 C=C-H bond around 3100 cm-1 that cyclohexane would not present.
PP 4-12 Answer: In order to answer this question we need to recall that the efficiency of a bond at absorbing IR radiation depends on strength of that molecule’s dipole moment. The bond with the largest dipole moment is the sulfur-hydrogen bond and therefore, should be the strongest peak in the IR spectrum.
PP 4-13 Answer:
The highest (largest) wavenumber in an IR spectrum would come from molecule
(c), the terminal alkyne. Stronger bonds tend to have higher frequencies and
since the alkyne has two bonding interactions making it a stronger bond than an
alkene or alkane, we see that its peak would be located at the highest
wavenumber.
PP 4-14 Answer:
(a) Compound (d)
(b) Compound (b)
(c) Compound (c). Recall that a molecule
needs to have a sp C-H bond in order to show a peak at 3300 cm-1 in
the IR. Compound (e) is an internal alkyne and is lacking the H attachment to
give this specific spectrum.
PP 4-15 Answer: (a) The IR spectrum of our starting materials would show a broad signal around 3300 cm−1. However, as our product started to form, we would still see the signal around 3300 cm-1 but we should see a strong signal start to appear around 1720 cm-1 for the carbonyl portion of the carboxylic acid. (b) The IR spectrum of our starting materials would show a signal around 3100 cm−1 for the sp2 C-H bond and a signal around 1650 cm-1 for the C=C bond. As the alkene is reduced to our product, these peaks should disappear.
PP 4-16 Answer:
![]()
PP 4-17 Answer:
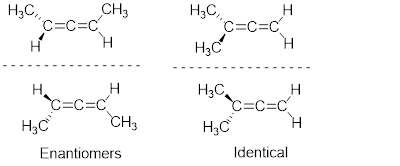
PP 4-18 Answer:
Is the molecule below chiral? Yes.
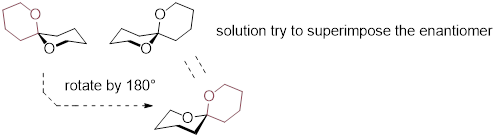
Does the molecule possess a chiral atom? No