CHAPTER 5. CHEMICAL REACTIVITY AND MECHANISMS

(Arthur Cammers and Ashley Jolly Steelman, University of Kentucky, 2019, with excerpts from Timothy Soderberg, “Organic Chemistry with a Biological Emphasis,” 2016)

Learning Objectives:

1. Why don’t automobiles use chemical energy in water to run? Where do you get the energy to get out of bed in chemical terms?

2. Predict the direction of chemical equilibrium using Gibbs free energy. (■■)

3. Describe factors that affect reaction rate. (■■)

4. Extract thermodynamic and kinetic information from reaction energy diagrams. (■■)

5. Understand that reaction energy diagrams can describe complex processes. (■■)

6. Explain the difference between stationary state and transition state. (■■)

7. Explain the term chemical intermediate. (■■)(■■)

8. Define thermodynamic vs. kinetic reaction products. (■■)

9. Define catalysis. (■■)

10. Identify electrophilic and nucleophilic sites in chemical structures. (■■)

11. Draw electron-pushing arrows showing the flow of electron density in a reaction mechanism. (■■) Remember to indicate electrons, and not nuclei moving.

5.1 INTRODUCTION TO CHEMICAL THERMODYNAMICS

(Arthur Cammers, 2019) Image: Rapid Air Oxidation of C₄H₁₀. Arthur Cammers, 2019

Up to this point, we have discussed the energies of electrons in molecules. Since some molecules do well at stabilizing electrons and others do not, molecules can be a place where electron energy gets trapped for later use—batteries, fat, food, gasoline, etc. We highlighted aspects of molecular structure that stabilize electrons in terms of minimum charge separation, bonding, π orbital conjugation, and electronegativity. When people talk about chemical change, they are talking about bonds breaking and/ or forming. This chapter unpacks the theory of how the high-energy electrons can become low-energy electrons in these chemical changes. From previous chapters and previous study of chemistry, we know not to occupy an MO with an electron if there is a vacant position at lower energy. This is how we filled the periodic table when we studied the structure of chemical periodicity in General Chemistry. The last chapters used similar guidelines to construct MO energy diagrams, by first populating the lower energy levels with electrons. The same electron-energy minimizing objective on the part of Mother Nature drives chemical reactions. Mother Nature favors systems of electrons in low-energy situations; this is most often the direction of spontaneous chemical change. In this chapter, we describe some of these chemical changes while we try to connect this electron-energy minimizing tendency with structure.

With the exception of wind generators, nuclear power plants, and the occasional nuclear bomb test, everything else you see that ‘goes’ is powered by chemical change. These are changes in the stabilities of electrons in molecules. Summarizing Chapters 1 – 3 broadly tells us that these changes can be tracked back to charge separation because all things chemical can be understood in light of the electromagnetic force. This summary also tells us that chemical change must be accompanied by changes in MOs because MOs describe bonding and their energies determine the stability of the molecule.

Because we love each other and worry about tomorrow, it can be uncomfortable to put ourselves, our humanity, in the mechanistic terms of chemical change. However, think about the following scenario. You have a run scheduled today; you wake up, stretch a bit, study a bit of Organic Chemistry and you gear up to run. While you are eating up the miles, you are exhaling and sweating H₂O and CO₂ from the metabolism of ■ glycogen stored in your muscles, and if you run long enough your body taps into your stored ■ fat. Let’s chemically simplify the fat as ■ butyric acid (a simple fat found in butter), and the glycogen as ■ glucose (simple sugar found everywhere, including blood).

(butyric acid) C₆H₁₂O₆ + (glucose) C₄H₈O₂ + 15 O₂ ───► 10 H₂O + 10 CO₂ + work + heat

Notice that we need to take in O₂ so that we can convert the molecules we use to do work into H₂O + CO₂; also notice that the products have electropositive C and H atoms bound to electronegative O atoms, whereas the reactants have many C−C and C−H bonds. Because we now have an appreciation for electronegativity, we know that the electrons are farther away from the nuclear charge and therefore the reactants (food) are higher in energy than the water and CO₂ that we expel. The decrease in charge separation powers our run. If you got here in your car, we can simplify the mixture of hydrocarbons in the gasoline you burned as octane and write an analogous equation. The decrease in charge separation from reactants to products also applies to the equation below and qualifies the ability of our automobile to get us from point A to B.

2 C₈H₁₈ + 25 O₂ ───► 18 H₂O + 16 CO₂ + work + heat

Some of the energy of these chemical reactions is converted to work, but you likely know that some of the energy must increase the temperature of the system and dissipate into the surroundings. This universal rule decreases the hypothetical efficiency of any engine. The fraction of the energy that must dissipate as heat is entropy. Situations can prevent this dissipation—it was hot and humid preventing the sweat from evaporating as you ran, or the hose popped off the radiator in your automobile causing the temperature of the engine to increase. Inefficient heat transfer can slow or stop the chemical reactions that we rely on to ‘make it all go’.

In the following text, bear in mind that the spontaneity of chemical change always sources the energy of electrons in MOs. Lifting a weight gives it potential energy in that it can later drop and in the process do work or produce heat, likewise, electrons falling in energy can do the same. Furthermore, since the absorption of light increases the potential energy of electrons, and photosynthesis traps that potential energy in molecules, the sun is (or has been) the source of nearly all the available chemical energy on the planet with few exceptions. In terms of how electrons get trapped in high-energy molecules, we know that the photosynthetic process must involve making high-energy bonds from lower-energy bonds. From previous arguments involving electronegativity and bonding, we have an idea about the atomic content and nature of those bonds. Let us pursue the nature of chemical change and its relationship to molecular structure.

5.2 REACTION ENTHALPY (ΔH_rxn)

(Arthur Cammers, 2019)

Let’s stop and think about where we’ve been and where we are at the moment. From Chapter 1 we know that the energy of the electrons determines all things that we can tag as chemistry or chemical. From Chapters 2 and 3 we know that the tendency of electrons is achieve lower energy by condensing around electronegative atoms and condensing in between atoms in bonds. The change in the energy of electrons upon any chemical change (changes in bonding, or changes in state: liquid, solid gas, solvation etc.) is called ■ enthalpy. When we showed the MOs of H₂ in Chapter 2 and discussed the bond strength of H₂, another word that we could have used for bond strength would have been ■ bond enthalpy. At this point we should have a good intuitive feel for the definition of chemical enthalpy.

5.3 REACTION ENTROPY

(Arthur Cammers, 2019)

The word entropy carries a lot of cultural baggage. Sometimes it gets framed as chaos, and other times as the tendency of teenagers’ bedrooms to get messy as the week progresses. These cultural ties to entropy are of little use to us. For entropy to serve us here, we need to frame the concept operationally. To do this, let us think about the ■ specific heat of a substance, which is the constant of proportionality between energy lost or gained and the change in temperature of the substance: ΔQ = m•C•ΔT where m = mass. There are differences in the values of heat capacities (C) of a single substance depending on how we measure it … whether at constant pressure or constant volume, for example. The heat capacity of a substance also depends on the state, so liquid water and ice have different heat capacities.

5.3.1 Entropy in Calorimetry

The specific heat of a material in units J•g⁻¹•K⁻¹ is the energy necessary in joule to increase the temperature of a gram of the material by 1 °C. If we put three items at 20 °C in thermal contact: copper beads (200 g), water (500 mL) and a thermometer, because they are at the same temperature there will be no transfer of energy; even though, these objects contain different amounts of internal energy. The ■ zeroth law states that no transfer of energy occurs between bodies at the same temperature, which justifies the application of thermometers to thermodynamics.

In the figure, we have a setup in a jacketed flask to prevent any heat from radiating into the environment. Now let’s run a thought experiment. Let’s say that the beads can magically change from a gram of Cu to a gram of Al in an instant. What would have to happen to the temperature of the isolated system?

To simplify the calculation, ignore the material in the thermometer and the flask—let’s say we can make these as thin as we want. The ■ specific heat of water, Cp(water) at 20 °C = 4.186 J /g•K. The corresponding values for Cu and Al are 0.386 and 0.900 J /g•K.

The calculation still must conserve mass and energy. The total energy given the temperature of the water and the Cu =

Q = 500 g• 4.186 J /g•K • 293.15 K + 200 g • 0.386 J /g•K • 293.15 K = 6.3619E5 J

After the magic change from Cu to Al.

Q = 500 g• 4.186 J /g•K • 293.15 K + 200 g • 0.900 J /g•K • 293.15 K = 6.6633E5 J

The energy of the system has magically violated the conservation law, to avoid this law breakage, the temperature of the system must drop. Realizing that 6.36E5 J is all the energy there is, the new temperature at equilibrium is:

T(new) = 6.3619E5 J ÷ (500 g• 4.186 J /g•K + 200 g • 0.900 J /g•K) = 279.9 K or 6.7 °C.

So the change in heat capacity means the temperature dropped about 13 °C.

5.3.2 Changes in Chemical Entropy (ΔS_rxn)

To demonstrate a temperature change in response to a magic change in the ability of a substance to absorb heat descriptions got a little strange in the section above. I did this because chemical reactions actually have the ability to change the way material absorbs heat. The reactant absorbs heat differently than the product. We have to have a way to account for this. We cannot simply believe that when we measure the temperature change due to a chemical reaction, that only changes in the energies of occupied MOs change the temperature. Think about what has to happen for a substance to increase in temperature: energy is transferred to the easily moved parts of the substance first and as the substance absorbs more energy stiffer parts of the substance move.

The more low-energy movements a molecule has, the more entropy is associated with the molecule’s constitution (ΔS_f).

Unlike specific heat, we cannot measure ■ molar entropy directly. This would take multiple experiments and approximations to sum molar heats and transition entropies (melting, boiling, etc.); click the link for more information. Thus, specific heats of substances are not the same as their molar entropies. However, the two molecular parameters have the same units (J/mol•K) and they address the ability of substance to contain heat based on the substance’s constitution at the molecular level.

A chemical reaction can change the way thermal motion (the movement of a particle associated with the particle's thermal energy) distributes itself on a molar basis (ΔS_rxn) from reactant to product by simply breaking the molecule in half.

A−B ──► A + B (ΔS_rxn > 0 = spontaneous)

In this case, we begin with A attached to B in the reactants but after the chemical change the products now contain two components that are bumping around in the container engaging in thermal motion. This means that the system can hold more energy at a given temperature after the reaction. Such a change is associated with a positive entropy change (ΔS_rxn > 0) which we recognize as a spontaneous reaction, meaning the reaction will occur. The universe tends to push the chemical change toward the A + B products. In this scenario the tendency of the universe to increase the entropy of the system breaks A−B bonds, and opposes the tendency of electrons to sit in lower-energy states (the definition of a bond). Thus, the chemical change tends to absorb energy from whatever it can to break the bond and this process cools the material. If the bond is strong enough (has low ΔH_f) the reaction will tend to favor A−B instead A + B.

Favorable positive entropic changes that oppose bond formation and thus cool the systems in which they occur are ubiquitous. The sweat that evaporates from your body as you run is a positive entropic change. Remember from previous discussions that hydrogen bonds in water partially bond one H₂O to others; evaporation must break these bonds. This process cools the surface from which the water evaporates due to the positive enthalpy of water evaporation. There are many water molecules mutually hydrogen bonded in liquid water; these connections are mostly broken in water vapor. When bonds form, the temperatures of the systems in which this occurs increases. When bonds break, the products absorb energy and the heat in the system has to decrease. Remember that bonds are, by definition, the decrease in potential energy of electrons.

Another example involving a ΔS_rxn > 0, would be a chemical change that allows increased bond rotation. An example would be a molecule beginning cyclic and then becoming acyclic. In the above A−B ──► A + B example, the changes in structure involve more atomic movement in the product than was in the reactant in the breakage of likely a π bond. Whenever you can ascribe greater ability of the product to move relative to the reactant, you can assume that ΔS_rxn > 0.

Conversely, chemical changes that run in the opposite direction, decreasing atomic degrees of freedom instead of increasing degrees of freedom, carry a negative sign on ΔS: (ΔS_rxn < 0). The universe tends to not favor these processes, an example of such a nonspontaneous reaction is A + B ──► A−B. Atomic degrees of freedom simply measure atomic ability to rotate, or move in x, y, z space. Six atoms bound in a molecule have fewer degrees of freedom than all six atoms released as a monoatomic gas, for example.

A + B ──► A−B (ΔS_rxn < 0 = nonspontaneous)

There are often exceptions to rules in organic chemistry. In the example below we see that the overall reaction goes from A + B ──► A−B. We might expect the chemical change to be characterized as a decrease in atomic-level freedom making ΔS_rxn < 0. However, we see experimentation indicates ΔS_rxn > 0. Upon examining additional experimental details, we see that A and B are highly solvated by water in the reactants and then undergoes condensation to a less solvated, perhaps less polar species. The key here is that the increase in degrees of freedom is on the part of the water molecules that are now less solvated and have more atomic motion at lower energy.

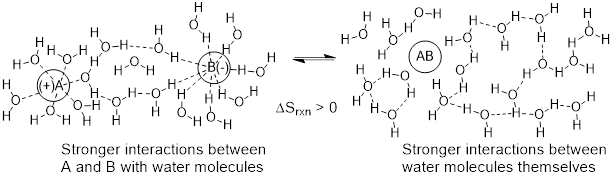
5.3.3 Universal Aspect of Entropy

In the absence of complicated issues, like solvation, the effect of bonding two molecules together or the effect of bonding an atom to a molecule should be associated with ΔS < 0. Likewise, when gasses condense to liquids and liquids to solids these changes strongly tend to involve ΔS < 0. We can feel this effect intensely when we step into a sauna and the steam condenses on our skin. Entering the sauna feels super-hot due to the extra heat delivered to us when hydrogen bonds form in the liquid water condensing on our skin. On the other hand, these effects can make ambient temperature feel hotter when the air is warm, humid and still. These effects can make ambient temperature feel colder when the air is dry, cold and windy. The opposition of Entropy to the stabilities of electrons in molecules (enthalpy, ΔH) makes the weather service provide us with real-feel and wind-chill factor temperatures so we can modify our expectations of the outdoor experience on any particular day.

Chemical changes that increase degrees of freedom in material are associated with relatively high positive changes in entropy, ΔS > 0. High positive changes in entropy are associated with spontaneous changes—if it ain’t tied down, it will fly away. Here, in the prediction of what is likely to happen next, the largeness of entropy goes viral in far-ranging aspects like determining the direction of the universal arrow of time etc. ■ Cosmological-Entropy, ■ Entropy-Means-Life-Must-Evolve, and ■ Shannon-Entropy of Information. Entropy is beyond chemistry; the heart of entropy is in the statistics of states of small components that are in thermal equilibria and such a thing must be universal!

5.4 GIBBS FREE ENERGY (ΔG_rxn) FOR CHEMICAL EQUILIBRIA

(Arthur Cammers, 2019)

In the entropy section, I’ve argued strongly for the deep and persistent tendency of the universe to favor changes that involve an increase in atomic /molecular level liberty. In the enthalpy section and in previous chapters, I argued for the tendency of electrons to favor bonding interactions. Because favorable enthalpy most often assembles, and because favorable entropy tends to disassemble, at some point Mother Nature must compromise between this manic behavior to make decisions regarding whether to stop or go. This compromise must intertwine with almost everything. Taking just one example … below the melting temperature, liquid substances spontaneously form favorable chemical interactions of one kind or another and solidify, opposing the molar entropy that favors the liquid state. This section on Gibbs free energy, characterizes and derives this universal compromise between entropy and enthalpy.

5.4.1 ΔG_rxn is A Difference in Entropy

The universe favors transitions characterized by increases in atomic-level liberty (ΔS > 0). The universe will tolerate transitions associated with negative entropy changes, as long as they are paid for by transitions associated with at least an equal magnitude of positive entropy change. This is the ■ 2^nd law of thermodynamics. Our earth is a beautiful and complicated condensed state comprised of many elements and liquid water. Life on the planet requires order in condensed phases and timing of chemical events that support life. However, our existence does not violate the thermodynamic 2^nd law because retribution is paid back to the universe. High-energy short wavelengths of solar electromagnetic radiation impinge on our ‘thermally isolated system’. By system I mean the earth, as the atmosphere gets thinner higher up, the planet no longer transfers heat from itself to the universe. Heat transfer requires molecular contact, but up there the concentration of molecules in the atmosphere slowly approach zero.

Thus, high-energy short wavelengths in the UV-visible region of the EM spectrum come into the system, and find their way into the atmosphere and biosphere as increased electronic energy—molecular motion, and then the energy is cast back out into space as low-energy long wavelengths in the infrared region of the EM spectrum. Very basically, many more photons are cast out than come in, and as we know from our phenomenological description of entropy, since the ‘out’ solar photons outnumber the ‘in’ solar photons, the sun’s EM relationship with the earth must be associated with ΔS > 0. ΔG_rxn relates directly to this kind of an entropic change in system vs. entropic change in surroundings. Our evolution and continued existence is favored by a ΔG on a grand scale.

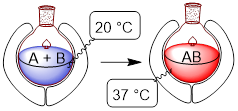The figure depicts conditions before and after a chemical reaction in a thermally isolated system in which A + B ──► A−B, with affiliated temperature change of an inert media. When we thermally isolate chemistry like this, the 2^nd law that applies to the universe, now applies to the inert media or solvent (the stuff that is going from blue to red in the figure) because heat is not transferred to the universe. We refer to this inert media as the surroundings. The material, A+B and AB, undergoing chemical change is referred to as the system. Now, both values can be easily measured.

(1) For the chemistry above to be spontaneous meaning that the reaction will occur, ΔS(rxn) needs to be a positive value.

ΔS(system) + ΔS(surroundings) > 0

Since in this case, the surroundings refer to the media in which the change occurs. Let’s just call the surroundings the solvent.

ΔS(system) + ΔS(solvent) > 0

(2) From the operational definition of entropy (small amount of heat added to something divided by the temperature): ΔS = dQ /T, so we can rewrite the conditions sufficient and necessary for spontaneous change by tracking entropy changes in the solvent.

ΔS(system) + ΔQ(solvent) / T > 0

(3) The ■ First Law of Thermodynamics states that the universe conserves mass and energy, so energy lost by the system is gained by the solvent. This lost versus gain of energy means that if the energy of the system is positive, that of the solvent is negative. Therefore, Q gained by the inert solvent measurable by ΔQ = Cp(solvent)•ΔT = the change in the potential energy of the electrons in the chemical reaction and that is just ΔH_rxn.

ΔS(system) − ΔH_rxn /T > 0

(4) Since we already stated that the system is the material undergoing change …

ΔS_rxn − ΔH_rxn /T > 0

(5) The function that we are going to define works better if we multiple through by −T.

ΔH_rxn − TΔS_rxn < 0

The inequality always flips when we multiple by negative numbers. 2 > 1, but multiplying both sides by −1 has a concomitant flip of the inequality: −2 < −1.

(6) The inequality above defines the sufficient and necessary parameters for a spontaneous chemical change. There are other hypothetical chemical changes we want to describe. We want to be able to state how far from the point of spontaneity a hypothetical chemical change is. So we define a function, ΔG_rxn = 0, where nothing happens. We realize that ΔG is now a characteristic of the state of material on either side of the chemical reaction just like ΔH and ΔS. We realize that ΔG_rxn is a gauge on how far away from spontaneous the chemical reaction is given the ΔG of products and reactants.

ΔH_rxn − TΔS_rxn = ΔG_rxn

The three expressions below are differences in thermodynamic parameters of formation. You will see these expressed as ΔHf (product), and ΔSf (molecule A).

ΔH_product – ΔH_reactant = ΔH_rxn

ΔS_product – ΔS_reactant = ΔS_rxn

ΔG_product – ΔG_reactant = ΔG_rxn

(7) The more negative ΔG be, the greater the tendency for chemical change is.

If ΔG_rxn < 0, then the chemistry is spontaneous … it might be very, very slow, but if Mother Nature CAN find a way for it to happen, it will happen. We say diamonds are forever, but the ΔG_rxn < 0 for C(diamond) ─► C(graphite). This tells us that diamonds are not really forever. Heat them up enough under normal pressures and they will convert to black soot.

If ΔG_rxn > 0, then the reaction is nonspontaneous. We can expect that the reaction will not occur.

5.4.2 Thermodynamic Parameters for Spontaneous Chemistry

We can use the Gibbs Free Energy equation to provide us with insight about a reaction. Using the information below, we can determine if a chemical reaction will proceed to form products or if the reaction will favor reactants.

(1) If ΔH_rxn < 0 (negative value) and S_rxn > 0 (positive value), then the chemical change is spontaneous and we can expect the reaction to occur because the overall value of ΔG_rxn will be a negative value.

ΔH_rxn − TΔS_rxn = ΔG_rxn

(-) − T (+) = (-)

(2) If ΔH_rxn > 0 (positive value) and S_rxn < 0 (negative value), then the chemical change is not spontaneous and we can expect the reaction not to occur because the overall value of ΔG_rxn will be a positive value.

ΔH_rxn − TΔS_rxn = ΔG_rxn

(+) − T (-) = (+)

(3) If ΔH_rxn > 0 and S_rxn > 0, then S_rxn contributes to spontaneity and H_rxn opposes spontaneity. Depending on the magnitude of the parameters, ΔG_rxn could be positive or negative depending on the temperature. Furthermore, these describe an endothermic reaction, one that has to absorb energy. This is what happens when water evaporates as described previously.

ΔH_rxn − TΔS_rxn = ΔG_rxn

(+) − T (+) = (+) or (-), answer depends on T

(4) A similar statement can be made for the case in which ΔH_rxn < 0 and S_rxn < 0. With small ΔH_rxn, the reaction could be entropically controlled and have Keq < 1, or not occur at all, depending on the temperature. Larger exotherms can drive condensation-type reactions, the kind of reactions we know to be characterized by S_rxn < 0, such as: A + B ──► A−B. We often add A and B together in chemical reactions to get products of greater molecular weight. For this we usually need the driving energy of large negative ΔH_rxn.

ΔH_rxn − TΔS_rxn = ΔG_rxn

(-) − T (-) = (+) or (-), answer depends on T

5.4.3 Using ΔH of Chemical Bonds

The average energies of bonds, ΔH, can be used to estimate whether reactions will be spontaneous. The specific energetic cost of breaking a C−C bond is dependent on the molecule, so even the C2−C3 bond breakage in heptane will be different than the C2−C3 bond breakage in octane. It is impossible to list the values for all bonds in all molecules so average values are listed (approx. ±4 kJ/mol) which allow us to approximate the energies of hypothetical chemical reactions. This value is termed the ■ bond dissociation energy (BDE), the energy required to break the bond between the two atoms. This is always a positive value because bond formation is defined by the electrons decreasing in energy as two atoms some together. In general, BDE informs us about the stability of molecules.

Bear in mind that the effect of ΔH_rxn on ΔG_rxn tends to be larger in magnitude than that of ΔS_rxn. In fact, in tables to estimate ΔG_rxn the ΔH_f (enthalpies of formation) are listed in units of kJ /mol or kcal/ mol. When entropic corrections are needed, they are listed in J /mol•K or cal/ mol•K units. This is three orders of magnitude difference; the entropy contribution has to be multiplied by T which is usually a small two-order of magnitude factor.

The bottom line: bond enthalpy or bond dissociation energy (same thing) can be used to estimate whether a reaction will likely run. The mechanism by which the atoms rearrange does not matter because ΔHf, ΔSf and ΔGf are state functions. ΔH_rxn, ΔS_rxn and ΔG_rxn are differences in their respective formation parameters so they are also state functions. By definition, these are path independent.

A−B + C−D ──► A−C + B−D

might go by

A−B + C−D ──► A(+) + B(−) + C(+) + D(−) ──► A−C + B−D

or by

A−B + C−D ──► •A + •B + •C + •D ──► A−C + B−D

Note: synchronicity (all bonds breaking and forming at the same time) in bond breakage is rare. The bonds most often break and form one at a time, but I am just indicating how they might break whenever they break.

We name these mechanistic pathways by how the bonds break: ■ heterolysis and ■ homolysis respectively. The fact that the thermodynamic parameters are state functions means that all you must worry about are the relative stabilities of the reactants and the products to estimate ΔH; you don’t have to worry about the mechanistic path that the bonds take to break.

You may have done some of these calculations in General Chemistry. To estimate whether the chemical reaction A−B + C−D ──► A−C + B−D is exothermic or endothermic we assign negative values to the tabulated bond strengths of the bonds formed in the reaction and positive values to the bond broken. Then we sum the values to estimate ΔH_rxn.

ΔH_rxn = bonds broken – bonds formed

Exercise 5.4.1 Consider the reaction below in which an alkane is converted to an alkene and H₂. The reaction is heated and catalyzed because it is very slow. The rate of the reaction does not necessarily mean that the reaction is disfavored. We’ll unpack this later. Calculate ΔH_rxn with the table of bond dissociation energies below.

H–H: 436 kJ / mol H–C: 414 kJ / mol

C–C: 347 kJ / mol C=C: 272 kJ / mol (pi bond only)

Exercise 5.4.2 The bond dissociation energies for the relevant bonds are given below each of the species involved in the following reaction. Calculate the overall ΔH° for the reaction.

(CH₃)₃C-H + Cl-Cl à CH₃)₃C-Cl + H-Cl

ΔH^o = 400 kJ/mol ΔH^o = 243 kJ/mol ΔH^o = 349 kJ/mol ΔH^o = 432 kJ/mol

Exercise 5.4.3 Consider the following reaction. (a) Use the table of bond dissociation energies in the problem above to estimate ΔH for this reaction. (b) ΔS of this reaction is positive. Explain why this is the case. (c) Discuss the most probable sign of ΔG at 20 °C.

Exercise 5.4.4 Determine whether equilibrium will favor the reactants or products based on the following information. Hint: what is the value of ΔG at equilibrium? Some answer may involve a qualifying sentence instead of just favor or disfavor.

(a) An endothermic reaction with a negative ΔS

(b) An exothermic reaction with a negative ΔS

(c) An endothermic reaction with a negative ΔS

(Exercises 5.4.1-5.4.4, Ashley Jolly Steelman, University of Kentucky, 2019)

5.5 EQUILIBRA

(Arthur Cammers, 2019)

The equilibrium constant is an expression of the ratio of concentration of product over reactant when the reaction stops changing. Since atoms and molecules are always bumping together, some fraction of the whole has a statistical chance of having enough collisional energy to undergo chemical change. Due to this fact, all studies of the rates of reaction are closely tied to the measurement, and control of temperature. My PhD adviser told me once when I was equivocating about whether a reaction was fast, “a fast reaction is one that happens on the human time-scale at 10 °C.” Comparing slow and fast reactions relative to the human observational timescale (hours to days) has us looking at extremes of reaction rates in units of M•sec⁻¹ that change by many ~10 orders of magnitude in either direction.

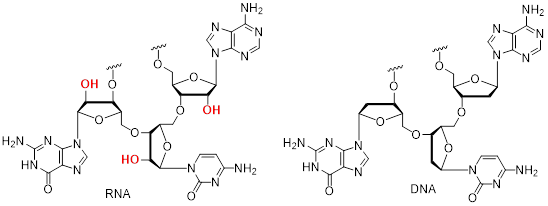
Small structural changes can have big effects on the rates of reactions. For example, examine the RNA and DNA biopolymers below. The D in DNA stands for deoxy because the ribose (sugar) unit of the polymer lacks an OH group at the 2’ position—see the structures below. Certainly, the most remarkable feature of the two molecules is their very different rates of degradation in pH neutral water, given the similarity of their structures. For RNA, the rate of ■ hydrolysis is more base pair sequence-dependence and is best measured in terms of hours. For DNA, there are fewer base pair sequence-dependence on the rate of hydrolysis and the rate is most comfortable measured in millions of years. This is the reason that we can store DNA forensic evidence and prosecute years later or determine the genome of prehistoric humans by drilling into ancient dentin found at archeological excavation sites.

5.5.1  ΔGrxn = −RTLn Keq

ΔG_rxn = −RT•Ln (Keq) is a familiar relationship between the reaction free energy and chemical equilibrium. The free energy and its equilibrium apply strictly to conditions in which some ratio of the reactants and products are present in a reaction; that is to say at conditions in which forward and reverse rate constants establish the ratio of reactants to products in real time. At other conditions, the difference in ΔG between two substances is an estimation.

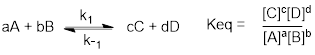
Since equilibria depend on reaction rates, deriving the relationship between ΔG and equilibria requires a derivation of the dependence on reaction rates and the energies of reaction pathways. Doing this right requires statistical mechanics. The statistical definition of entropy (S = k • Ln W) is the reason the natural log is involved in the equation. We are not going to take the tangent necessary to derive the equation.

However, the ability of chemical reactions to run to practical completion, even with fairly small ΔG_rxn is an aspect of the equation that you should appreciate. Numbers are not real to people unless they know whether the number is relatively large and significant or small and less significant.

Sophisticated quantum mechanical calculations have an associated error of about 3 kJ/ mol. So, that is a small number for ΔG_rxn. The ΔG_rxn above, 8 kJ /mol, is also a small number, given the range that organic reactions have in reaction free energies. A moderate number might be the free energy involved with folding an average ■ globular protein into its functional native state: ΔG_fold: 20 - 60 kJ /mol. A big number might be the free energy involved with forming covalent bonds in the average organic molecule: ΔG_bond: 250 - 500 kJ /mol. Let’s do a calculation with the small number involved with the conversion of Z to E alkenes. Let’s choose 25 °C for a temperature.

ΔGrxn = −RT•Ln K_eq K_eq = InvLn (ΔG / RT)

K_eq = InvLn (8 kJ/mol / 8.314 J/mol•K / 298 K • 1000 J / kJ) = 25.3

Remember that we discussed alkene isomerization to require billions or billions of years. A catalyst would be needed to establish equilibrium at 25 °C, but when this is reached the expected ratio of Z : E would be 1 : 25.3. The mixture would be 1 / 26.3 x 100% = 3.8% Z and 96.2% E.

The example above means that we could cleanly synthesize (E)-3-hexene from (Z)-3-hexene or really any sloppy mixture of the two.

Have an appreciation of the fact that two methyl radicals will react to form ethane with a very negative ΔG.

•CH₃ + •CH₃ ──► C₂H₆, ΔG ~ −300 kJ /mol

Such a large negative ΔG value means there is no methyl from the reactants in the mix. The reaction runs to completion and equilibrium favors the right as written. In fact, realize that this reaction has to be hypothetical. We could never keep methyl apart and then at some point allow the reaction to run. Methyl would have to be generated on the fly and as soon as it appears it would combine with itself to form a dimer (dimerize).

5.6 KINETICS

(Arthur Cammers, 2019)

The wonders of ■ statistical mechanics in the development of ■ transition state theory was required to derive the relationship between ΔG and K_eq because these come from a ratio of two rates. It is the expression of the rate constants in terms of energy that is derived. You will have to wait for a more advanced class if you have not been into this science already. To carve out a useful concept of chemical kinetics, we will use the overall results of the calculations. Think about the following notions.

Molecules of different energies in one bottle do not necessarily react. Why is this so? Shouldn’t Mother Nature find the best, lowest energy situation for the electrons in these molecules that she could, especially given her tendency to chaos? If the universe really worked this way, the molecules and the chemical processes that support life would quickly dissolve into this chaotic soup.

Molecules trap electronic energy in wells, and getting between wells means getting from one molecule via a chemical reaction to another molecule. This always involves going over an energy barrier. If there is not enough energy in the system to get over the energy barrier then the reaction will not occur. The height of this energy barrier determines how fast reactions happen.

A ──k──►B

Here, k is not the equilibrium constant; it’s the rate constant.

This is the ■ Eyring equation, where k_t = transmission coefficient (usually 1), k_b = Boltzmann Constant, h = Planck Constant, ΔG^‡ is read as the free energy of activation, and ΔG^‡ > 0.

The rate of the chemical reaction = k[A], the lower the intrinsic energy barrier to the reaction (ΔG^‡), the faster the reaction runs.

The state of the material at the top of the energy barrier is referred to as the transition state and denoted with ‘‡’. This kinetic barrier, ΔG^‡, is the energetic difference between the ΔG_f (free energy of formation of the reactant) and the free energy of the transition state.

5.6.1 ΔG^‡ is Not a State Function!

In the preceding sections, we used the enthalpies of bond formation to estimate the stabilities of molecules. We could do this because we did not care which path the molecule took to show up. These enthalpies were characteristic of the state of the electrons trapped in molecule 1 versus the state of the electrons trapped in molecule 2, and therefore path-independent.

When ΔG_f(reactant) is compared to ΔG_f^‡(homolysis), the energies of the barriers are drastically different than when ΔG_f(reactant) is compared to ΔG_f^‡(heterolysis). How the occupied MOs of the reactant transform differently in these two pathways determines the energies at the top of these barriers as the atomic parameters of the transition state structure is reached. Remember that the atomic parameters determined how the atoms in a molecule were disposed in space, whether atoms are coplanar or pyramidal, etc. These atomic parameters included bond length (2-atom), bond angle (3-atom), and dihedral angles (4-atom). There are transition states that the MOs allow, and others that the quantum mechanical rules forbid.

The bond dissociation energies are applicable to chemical path, homolysis. Thus, the bond dissociation energies of H−Br, and C−H would be applicable toward the kinetics of H₂C=CH−CH₃ + Br• à H₂C=CH−CH₂• + HBr in the gas phase or inert solvents, but would have next to nothing to do with the hypothetical kinetics of a heterolytic process involving the breakage of these bonds.

The kinetic energy barrier is a function of the mechanism. Like the shape of molecules was followed with atomic parameters, the chemical pathway that molecules follow to transform into other molecules is also tracked by atomic parameters. Like the energy of molecules changed with atomic parameters, the energy of the chemical pathway also changes with atomic parameters.

5.6.2 Molecular Features that Affect Reaction Rates

For a molecule to react selectively, there must be a low-energy pathway for it to transform from reactant to product, and this is set by MOs. We followed how various MOs changed in Chapters 2 and 3 with MO energy diagrams. Molecules that are reactive, that hold their electrons at relatively high potential energy will tend to react. We need to change the conditions of molecules to get them to react by taking them out of the freezer, or warming them from room temperature to reaction temperature, or taking them up from the solid state into solution, or shine light on them—all of this depends on the molecule and what we want the substance to do.

The reaction above is a unimolecular reaction (a reaction where a single molecule produces one or more molecules of product); look at exercise 5.4.3 above for a specific example (B can be more than one molecule). The amount of material that converts over time is given by the unimolecular or first order rate law:

Rate = k [A]

If molecule A is kept at a temperature that keeps the internal energy of the media low enough, the molecule will not absorb enough energy via molecular collisions to take that low-energy pathway of electronic change to molecule B. At some temperature however, perhaps a solvent molecule hammers into A and it breaks at its weak point.

The reaction above is a bimolecular reaction; here two molecules have to collide to make the product. The amount of material that converts over time is given by the bimolecular or second order rate law:

Rate = k [A][B]

Here, what concerns us most is that initial collision. Everything we said about controlling the rate for the unimolecular reaction applies to the bimolecular reaction. Furthermore, just a little math will convince you that if the concentration of B = 0 the reaction will not run, so increasing the concentration of B (and /or A) will enhance the reaction rate.

The rate constant is also dependent on steric considerations. If a molecule is sterically hindered (a molecule possessing such large or bulky groups that it prevents or delays a chemical reactions) it can affect the overall reaction by slowing the reaction rate.

For A and B to click to make C, the atoms must slam together and get within near bonding distance of each other. Repulsive interactions between nonbonded electrons (■ steric effects) can strongly prevent the closing of this distance between atoms and prohibit bonding. We are going to unpack this issue later in greater detail, but at first glance, and rightly so, you might expect that electrons pushing each other away might promote some unimolecular reactions like:

A−B ──► A + B

You do not have to know anything about how the reaction runs to realize that the product is challenged by the steric interaction of the two fully substituted C atoms adjacent to each other. In the case above the steric effect prevents the equilibria of the reaction from favoring the products.

5.7 INTRODUCING ENERGY DIAGRAMS  

(Arthur Cammers, 2019)

In a manner similar to the way we represent MOs and their energies in MO energy diagrams, it is intellectually advantageous and helps us communicate with each other, to represent reaction pathways in reaction energy diagrams. In the diagram below we graph free energy of formation ΔG_f on the vertical axis and the reaction coordinate on the horizontal axis.

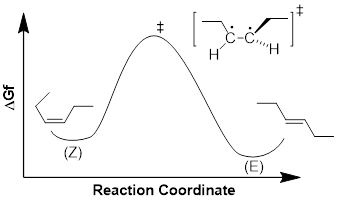
The diagram above represents the reaction energy diagram for the interconversion of Z and E alkenes. We should first examine the C2C3=C4C5 dihedral angle of the double bond in (Z)-3-hexene. As the dihedral angle goes toward 90° the CC π bond breaks until the interaction between pz orbitals = 0 in the transition state. Because we know that the stability of the C=C is about 270 kJ /mol we know that the transition state is 270 kJ /mol higher in energy than the starting reagent, (Z)-3-hexene. As the dihedral angle increases further, the p orbitals begin to interact more strongly, decreasing the energy of the molecule until at 180°, the CC π bond is fully reformed and we reach the (E)-3-hexene. From the reaction energy diagram, we can read the following:

· The barrier to the conversion of Z to E (path-dependent). This determines the rate of the reaction as written.

· The barrier to the conversion of E to Z (path-dependent). This determines the rate of the reverse reaction.

· ΔGrxn (path-independent) determines the equilibrium.

These are shown below.

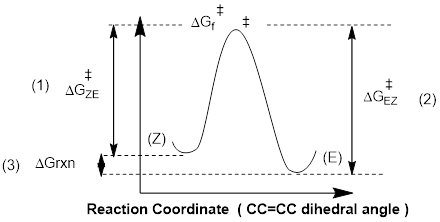
We can see that the reverse pathway from E to Z is of higher energy than the ZE path, meaning the EZ path is not as fast as the ZE path. This should be intuitive since we calculated that at equilibrium determined by ΔGrxn we have a 25 : 1 excess of the E material. Since Keq is a ratio of two rate constants, and since the higher energy slows one reaction down relative to the other, Keq = k_ZE /k_EZ > 1.

We need to appreciate something else about the reaction energy diagram. Progressing along the reaction coordinate, the energies in the pathway turn three times at three chemical species of interest, 1) the Z alkene, 2) the transition state and 3) the E alkene. The E and the Z alkene are referred to as stationary states. The material oscillates in these energy wells, stretching and bending bonds, and rocking dihedral angles. The existence of the E and Z alkene is defined in time, they temporally oscillate about a set of ideal atomic parameters that are on the reaction coordinate. They also oscillate about a set of atomic parameters that are off the reaction coordinate. The Z and E alkenes are structures with defined energy minima.

On the other hand, the transition state does not oscillate about a set of ideal coordinates because the electrons in the structure will slip down toward the stationary states with any change in the reaction coordinate. The transition state does not have a defined existence. It can be said to exist for only an instant, and instants are temporally undefined. When does that baseball that you throw up into the air begin to return to your hand? This temporally undefined condition is the nature of the transition and if you give it a moment’s thought … you’ll realize that all stationary states must be separated by transition states.

Since we talked about another reaction above H₂C=CH−CH₃ + •Br à H₂C=CH−CH₂• + BrH, let us frame the energetics involved in terms of the reaction energy diagram. This should shed light on some of the corners that perhaps the first example left in the dark.

The relevant bond dissociation energies are: H−Br 366 kJ /mol and H2C=CH─H2C−H 356 kJ /mol.

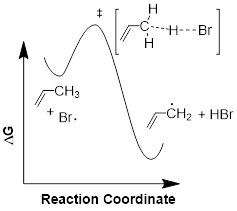
This reaction coordinate is multiparametric (having multiple parameters). From the reactant, as the C−H bond breaks, the structure increases in energy as the transition state evolves. However, the partial formation of the H−Br bond decreases the energy of the transition state. The CCHH improper dihedral angle begins to flatten. In the process of planarization, the CC, and two CH bonds acquire more s character in going from sp³ to sp², and the orbital on the C atom with the odd electron forms an allylic πMO system which recovers some bonding energy.

So the C−H partial bond breakage takes the electrons up in energy, but H−Br partial bond formation and the planarization of the radical brings the electrons down in energy. Taken together (the radical + HBr), this collection of molecules would have to increase in energy to change anything, it is a stationary state, a chemical intermediate. Yes, more than one species can occupy a position on the reaction energy diagram. When we get more sophisticated, we will on occasion have to include solvent molecules and energies absorbed from photons in these curves.

5.7.1 Kinetic vs. Thermodynamic Products

(Arthur Cammers, 2019)

The path dependence of transition state-dependent kinetic processes means that the most stable product that is produced by a reaction is not necessarily the most abundant product made by the reaction. The most stable product is the most abundant product only if the conditions set up an equilibrium between reactants and products. In this case the tendency of electrons to find the lowest point will drain down to the most stable enthalpies and entropies in terms of chemical bonds, lone pairs and atomic degrees of freedom.

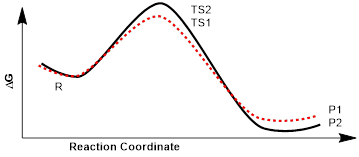
If the chemist makes sure that conditions do not favor equilibration, then the product that is connected to the lowest-energy transition state will be the product in most abundance.

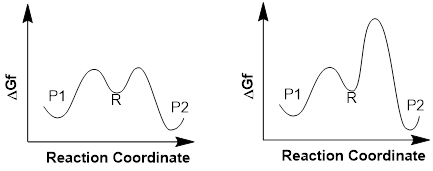
The reaction energy diagram on the left will favor the thermodynamic product P2 because the transition states that connect reactant, R, to P1 and P2 are low and P2 is the most stable product. In this case material going over either barrier and coming back to R is likely.

On the other hand, the reaction energy diagram on the right will favor the kinetic product P1; even though P1 is higher in energy than P2. The high kinetic barrier to the production of the thermodynamic product, the molecule of lower energy, P2, means it will not evolve in the absence of equilibration of all three molecules. (1) The thermodynamic product is always the lowest-energy product in an equilibrium. (2) The kinetic product is the product with the lowest energy transition state. The highest-energy product is not always the kinetic product. The kinetic product is the product that results if the reactant and products are not equilibrating. In this case the kinetic product is material that passes through the lowest energy transition state regardless of whether it is more or less stable than any other possible product.

5.8 READING ENERGY DIAGRAMS  

(Ashley Jolly Steelman, 2019) 

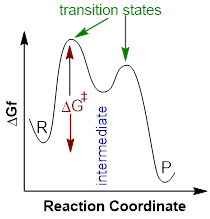Let’s get familiar with the terminology of an energy diagram. If a reaction involves multiple steps, the energy diagram will look like the diagram to the left. In order to get to the products (P) an energy barrier must be overcome. The height of this energy barrier is termed the activation free energy (ΔG^‡) and is responsible for the kinetics of a reaction. The greater the activation energy the slower the reaction will proceed. The top of any peak on an energy diagram depicts a transition state (TS), a point in the reaction where bonds are in the process of breaking and/or forming. The transition state is an activated complex and cannot be isolated (does not have any definable lifetime). Intermediates, on the other hand, can be isolated and are lower in energy than the TS. Intermediates are represented by high-energy valleys in the energy diagram. Now that our terminology is in check, let us study an example using a specific reaction. What can we learn about the reaction itself from the energy diagram?

Example 1: Examine that energy diagram below and answer the following questions:

a) How many steps does this mechanism have?

b) Which locations represent intermediates?

c) How many transition states are shown?

d) Is the overall reaction endothermic or exothermic?

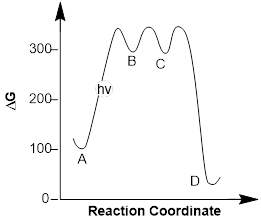
Solution: Without knowing the specific details of the mechanism we can decipher a ton of information about the process by examining the energy diagram. We can quickly answer questions (a) and (b). Each energy well represents the formation of an intermediate and there are two of these (B and C) and one product D. This tells us that the mechanism has 3 total steps; a step to form each intermediate and one step to form the final product.

The transition states are represented as energy maxima. There should be a transition state (a point where bonds are breaking and forming) for each step of the reaction and therefore, we see that there are three transition states.

The energy of the products is lower than that of the reactants and therefore, the reaction is exergonic (∆G_rxn < 0). If we calculated the free energy of the reaction, we would see that the ∆G_rxn would be negative since products D or E are lower in energy than reactant A.

Let us examine the mechanism for this energy diagram to confirm our answers. The mechanism below shows a radical reaction that we will discuss in more detail later. The three reaction arrows represent each step of the mechanism.

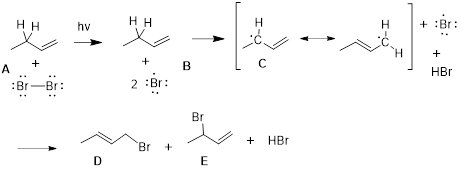
Since bond enthalpies are discussed above, you can look at this overall process and explain why the overall reaction is exothermic (try to calculate ∆H^o), specifically why the products are more stable (lower in energy) than the reactants.

Exercise 5.8.1 Use the bond strength table below to determine if the reaction is exothermic or endothermic and estimate the magnitude. Ignore the contribution of hv.

Bond	Energy (kJ /mol)
Br─H	366
Br─Br	192
H2C=CH─CH2---H	356
H2C=CH─CH2---Br	257

5.9 CATALYSIS 

(Arthur Cammers, 2019)

Consider the reaction energy diagram of a hypothetical chemical reaction that goes from reactant to product through a transition state. The reaction may not run on anything analogous to the human time scale because ΔG^‡ appears to be quite high. This is a similar situation to our description of the Z to E isomerization of the alkenes. The uncatalyzed process just does not allow the other isomer to evolve.

However, when I₂ is added to (Z)-3-hexene the concentration of the E isomer slowly increases over time.

As you know the π bond can act as an electron donor and the Iodine is fairly electronegative, giving I₂ a low-energy σ* orbital to serve as an electron acceptor.

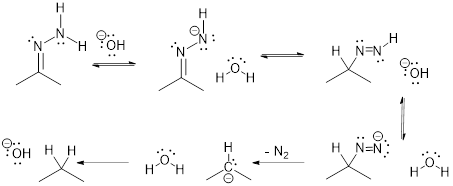
You may be inclined to draw a carbocation (a structure with formal charge on C) after the C−I bond forms, but iodine has a large covalent radius. This allows the iodine atom to just sit between the two C atoms as the intermediate with positive formal charge on iodine (epiiodonium ion). Eventually two iodine atoms bond to the CC chain. A few more elemental steps result in the regeneration of the starting iodine and the evolution of the E alkene. Since the iodine starting atoms are regenerated they can operate again and transform many more alkenes from Z to E. In this case the iodine atoms are the catalysts for this chemical reaction. The fact that they are not consumed by the reaction is a distinguishing characteristic for a catalyst.

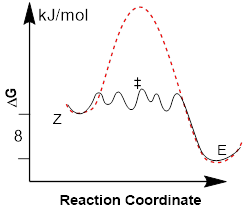The new reaction energy diagram has dramatically changed. The reaction coordinate is quite different, we have more atoms involved … the same TS cannot be on the same horizonal axis, but we project it there in red in the diagram at left to show how the energetics of the process changed.

The highest energy barrier determines the reaction rate, measured from ΔG_f (Z-alkene) to the highest-energy transition state. The bonding in the multiple intermediates above led to lower-energy steps for the eventual isomerization of the double bond geometry. Multiple catalytic steps dimple the reaction energy diagram with a series of stationary states connected by low-energy transition states. ΔGf ((Z)-3-hexene) and the ΔGf ((E)-3-hexene) did not change from that of the uncatalyzed reaction. Catalysis is just another specific path that changes the kinetics, but the stabilities of the isomers are state functions—these are always path independent.

There are many catalysts for a wide variety of chemical reactions. Whether these are enzymes catalyzing chemical reactions necessary for life processes inside our bodies, or whether this is some industrial process producing polypropylene from a gas phase feed stock, all the ■ reaction energetics of catalysis operate similarly. Interactions between catalyst and the molecules of interest install low-energy stationary states (chemical intermediates) on the reaction energy diagram which are connected by low-energy transition states to the product.

As most of you know DNA codes for RNA and RNA codes for protein. Much of the coded protein ends up as enzymes. These are chains of protein that fold in particular ways to imbue the chain with catalytic activity for particular biochemical reactions. Enzymes are named for what they do and the ■ list of types of enzymes is long—don’t worry you won’t have to commit any of that to memory, but I hoped you clicked the link and I hope you were impressed. ■ Genetic disorders can underproduce or in some cases over-produce any of these enzymes leading to various disease states or death.

The multi-national, multibillion-dollar, pharmaceutical industry is dedicated to make money trying to fix things. They develop small molecule drugs that block active pockets in enzymes to prevent them from functioning—to prevent any one of the intermediates in the catalytic mechanism from occurring and thereby blocking activity. Certain drugs can even bind to non-active portions of the protein chain to increase the activity of the enzyme. The application of all this is so incredibly broad that we can’t touch it all.

(1) Think about developing a small molecule to prevent the human immune deficiency virus from forming by blocking its ability to make one key protein necessary for the formation of the virus ■ capsid. (2) The main enzyme, ■ thyroid peroxidase responsible for over-active thyroid glands can be moderated with ■ small molecule drugs. (3) Fomepizole blocks the activity of alcohol dehydrogenase. This enzyme metabolizes alcohols to much more toxic molecules, namely their respective aldehyde metabolites. In cases of acute poisoning with antifreeze your dog might be treated with fomepizole to slow the conversion glycol to its toxic metabolites by blocking the active site of ■ alcohol dehydrogenase. Referring back to the catalytic reaction energy diagram, developing a drug that binds more strongly to the enzyme active site than does the natural substrate, prevents the catalyzed reaction from happening. Occupation of the catalytic site by the drug blocks entry to the substrate. Since substrate cannot get in, substrate cannot convert to product via these low-energy stationary states on the catalytic reaction energy diagram.

Exercise 5.9.1 Examine the reaction energy diagram; pick the best description.

(a) exergonic reaction (ΔG < 0) with bonds breaking and forming at the same time

(b) bimolecular endergonic reaction (ΔG > 0)

(c) exergonic reaction (ΔG < 0) with a bond-breaking step then a bond-forming step

(d) catalyzed exergonic reaction (ΔG < 0)

(e) exergonic reaction that forms two diastereomers

Exercise 5.9.2 Examine the energy diagram below and answer the following questions using the abbreviations for each position on the graph. Note that the reaction coordinate for these two reactions cannot be on the same horizontal axis, but people draw reaction diagrams like this all the time. One curve is simply seen as a projection onto the same axis from a different axis.

(a) Which product is the thermodynamic product?

(b) Which product is the kinetic product?

(c) Would the two products be formed in an equal ratio (1:1) at equilibrium? Explain your reasoning.

Exercise 5.9.3 Consider this equilibrium. How will diluting the likely change the equilibrium constant from conditions in which Keq = 1? A−B A + B

(Exercises 5.9.1-5.9.3 Ashley Jolly Steelman, University of Kentucky, 2019)

5.10 USING pKa TO PREDICT HETEROLYTIC BOND FORMATION

(Arthur Cammers, 2019)

The next section deals with heterolytic reactions in which fully occupied orbitals in nucleophiles and unoccupied orbitals in electrophiles combine to make σ and σ* MOs, the anatomy of covalent bonds. You will be asked to predict the way the molecules will react. To do so you will need to know how to gauge reactivity of the HOMO of a nucleophile.

The pKa of the conjugate acid that used the HOMO in the formation of the X−H bond is a measure of the reactivity of the nucleophile.

Why should this be so? You are likely familiar with pKa as a gauge of the strength of acids.

HA (+)H + (−)A pKa HA = x

In which case the lower the value of x, the stronger the acid. The more the A part of HA tends to give up the (+)H. If x is small, then the equilibrium lies to the right. If x is larger, then the equilibrium tends to the left as written above.

To understand why this is so you need to understand what is happening in the reaction above. How would we frame this is reaction in terms of MOs?

In the reaction above the HOMO lone pair of A and the 1s AO of ⁺H become σ and σ* of H−A as the reaction runs from right to left. Of course, this reverses as the reaction runs from left to right.

Remember that to combine two chemical species we need the driving energy of unstable electrons, and this driving energy is what the pKa is measuring. If you are wondering which pair of electrons will react, do a thought experiment, in which you protonate one electron pair and look up the pKa of the acid created. Then protonate the other electron pair. The conjugate acid that has the highest pKa will have the more reactive (higher-energy) corresponding HOMO.

It is easy to find extensive pKa data on the internet due to its power to inform about chemical reactions. A good broad pKa characterization of the organic molecules we will look at this semester can be found in ■ David Evans pKa Tables.

5.10.1 pKa is an Energy Unit

It is easy to say that pKa is an energy unit, and it is easy to rationalize as in the text above, but this one is also easy to derive, given the fact that I am talking to people who know about Bronsted acidity from General Chemistry.

The acidity constant is K_a = [A][H₃O]/[AH]

Thus, K_a = K_eq[H₂O] for the ionization in water

AH + H₂O A(−) + H₃O(+)

Taking the log of both sides and multiplying by −RT gives:

Why … because we can …

−RT•logK_a = −RT•log(K_eq[H₂O])= −RT•logK_eq – RT•log[H₂O]

Realizing that Log₁₀(x) = Ln(x) / Ln(10) remember that Log_b(x) = Log_d(x) / Log_d(b)

and

Ln(10) = 2.30

−RT•logK_a = (−RTLnK_eq − RTLn[H₂O])/2.30

but –logK_a = pK_a and –RTLnK_eq = ΔG

and RT•Ln[H₂O] is a constant

2.30RTpK_a + RTLn[H₂O] = ΔG

When comparing two chemical reactions we can subtract the expression above to get:

2.30RT ΔpK_a = ΔG₂ −ΔG₁ = ΔG_rxn

Example

Let’s determine which of the two reactions below is more exothermic.

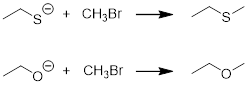
Solution

To answer this question, we can subtract one reaction from the other or add the reverse of one reaction to the other reaction.

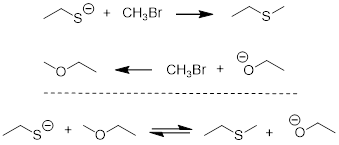
Even though the resulting equation is not fast enough to ‘happen’, the energy barriers are too large, ΔGrxn will still tell us which side of the equation is higher in energy, and we can estimate ΔGrxn from the ΔpKa.

Looking around in the pKa table, we find EtOH pKa = 15.9 (Wikipedia) and EtSH pKa ~10.5 (used the value for BuSH).

ΔpKa = 15.9 – 10.5 = 5 (as written always products – reactants)

2.30 • 8.314 • 298 • 5 = 2.85E4 J /mol = 28.5 kJ /mol = ΔG_rxn

This number expresses the free energy we can expect to get out of (-)OEt vs. (-)SEt as nucleophiles. The fact that ΔG_rxn > 0 mean that O atom nucleophile will tend to push the reaction to the right more than the S atom nucleophile in our original question.

The number above is for one of the electron pairs in the reaction, the lone pairs on opposite sides of the equilibrium. If you really want to answer how favored or disfavored the reaction above is, you also have to consider the other lone pair. That was not our original intent however, but let’s do this anyway.

The other electron pair is in the C−S bond, or the C−O bond depending on which side of the equation you look. Remember that these enthalpies are state functions.

Bond strength: C−S: 259 kJ /mol C−O 358 kJ /mol

−259 + 358 kJ /mol = 99 kJ /mol = ΔH_rxn ~ ΔG_rxn

99 kJ /mol + 28.5 kJ /mol = 127.5 kJ /mol ΔG_rxn should be an approximate heterolytic correction to the homolytic ΔH_rxn ~ ΔG_rxn.

5.11 NUCLEOPHILES AND ELECTROPHILES

(Ashley Jolly Steelman, 2019)

Nucleophiles and electrophiles are the players in ionic organic reactions—heterolysis, the breakdown of a compound into oppositely charged ions. If you are able to recognize which reactant has a site of high electron density and which reactant has a site of low electron density this is where you can expect a reaction to occur. However, these reactive partners must also have HOMOs and LUMOs. Electrophile means ‘lover of electrons’; in order to accept an electron, the electrophile must have an empty orbital at low energy. Nucleophile means ‘lover of nuclei’; to establish a bond to the empty orbital in the electrophile, the nucleophile must have available electrons, and Mother Nature can get more of an exotherm out of the reaction if these electrons are high in energy. Examine the electrostatic potential maps for the two molecules below.

methyl carbocation hydroxide anion

The carbocation’s carbon atom is a site of low electron density, but more importantly is has an empty orbital. It only has six electrons surrounding the carbon atom, right? We know from all the Lewis structures we have drawn that its lack of an octet makes it reactive! This empty orbital is a place for electrons to go and that makes methyl cation electrophilic. Do you remember what this empty orbital is? How is it hybridized? That was a trick question. This empty orbital is not hybridized at all, is it!

Hydroxide (^-OH ) is an anion with high electron density (nucleophilic), and a fully populated octet. If you draw the bond-line structure and put the lone pairs on the structure, you can see that there are three electron lone pairs on the oxygen atom. Any of these can serve as the HOMO for the reaction that you might draw between electrophile and nucleophile for this reactive pair of molecules.

Since we know that opposite charges attract, these molecules are drawn toward one another. But because one has an empty orbital, and the other has occupied orbitals the two molecules will react with one another to form a bond and an antibond. We will find this formula repeated in reactions of a nucleophile attacking an electrophile.

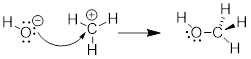
Given what I told you about electron pushing in previous chapters, this mechanism must involve electrons of the nucleophile in a HOMO establishing a bonding interaction with the LUMO of the electrophile. The MOs, HOMO and LUMO, of the reactants become σ and σ* of the C−O bond in the product. Since we are looking at two MOs, which convert, we must be able to follow their conversion to two MOs in the product by orbital conservation rules.

What is a nucleophile? The nucleophile is a high-electron-density atom (electron rich) capable of donating a pair of electrons due to its high energy HOMO.

Examples:

The nucleophiles in the figure above are from strongest on the left to weakest on the right.

Note: How is an alkene a nucleophile? The π bond is electron rich. The π electrons of the double bond are relatively far from the nuclei and are loosely bound compared to σ bonds. This was discussed in the chapter on π bonding. Therefore, the pi electrons can react with an electrophile. Remember that the π bond is the HOMO in hydrocarbon alkenes because π (parallel) orbital interactions are not as good as σ (head-on) orbital interactions.

What is an electrophile? The electrophile is a low electron density atom (electron poor) capable of accepting a pair of electrons due to its low-energy LUMO.

Examples:

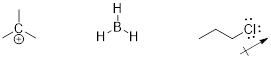
In the leftmost structures the unoccupied orbital is the p orbital at C and B atoms respectively.

In the structure at right the unoccupied orbital is the σ*CCl MO. It is low-energy due to the electronegativity of the Cl atom.

The electrophiles in the figure above are from strongest on the left to weakest on the right. The σ* MO is still a high-energy unoccupied orbital and its occupation by electrons will disrupt σCCl, right?

Note: Even though chlorine has three lone pairs, it is not a good nucleophile! The electronegativity of Cl stabilizes these sp³ orbitals of the lone pairs so the electrons are less able to donate to an electrophile. The electronegativity of Cl also pulls electron density away from the C atom. This ■ induction in alkyl halides makes the carbon atom electrophilic. The chlorine atom pulls electron density away from the carbon leaving it with a partial positive charge, and decreasing the energy of σ*_CCl. These electronic aspects render haloalkanes electrophilic at the C atoms.

Example: In the following reaction label the nucleophile and the electrophile in the reactants side of the equation.

Solution: Recall, when we are looking for the nucleophile, we are looking for a region of a molecule with relatively high negative charge (a π-bond or a lone pair). We can see that on molecule B the carbon bears unbound electrons. This is where we can expect our HOMO in the nucleophile. The lone pair on the O atom in molecule A might have been a logical choice, but these are less reactive than the lone pair in B. To test this, we can look at the pKa of the conjugate acids. The lower pKa tells us the electrons are more stable and less reactive.

As for the electrophile, we are looking for a region of a molecule with relatively high positive charge (a partial positive charge due to inductive effect or an empty p orbital). If we examine the resonance structure of acetone (A) we will find that a carbonyl group bears a partial positive charge at the carbon. This is where we can expect our electrophile to be located. The LUMO is associated with the π* of CO. This empty orbital is not so high due to the relatively weak π interaction and it is stabilized further by the electronegative effect of the O atom. The π* MO in cyanide (⁻:C≡N) are not as low-energy due to the decreased electronegativity of the N atom.

Upon examining the overall reaction, we can clearly see that the nucleophilic carbon (B) has attacked the electrophilic carbon of A to form the product shown. This was predicted by looking for the lowest energy LUMOs and the highest energy HOMOs to match for the reaction.

Exercise 5.11.1 Which molecule / ion drawn is the best electrophile?

Exercise 5.11.2 Which of the following molecules can serve as a nucleophile?

Exercise 5.11.3 In the following reaction, label the nucleophile and electrophile on the reactants side of the equation.

Exercise 5.11.4 In the interaction of the sodium and chloride ions in sodium chloride, given that the sodium ion obviously has an unoccupied orbital and chloride has HOMOs, why is there no covalent bond formed?

Exercise 5.11.5 For the following reaction that we previously discussed, how would you tell if the equilibrium favored the right or the left side of the arrow? Explain step by step what you would do.

(Exercises 5.11.1–5 Ashley Jolly Steelman and Arthur Cammers, University of Kentucky, 2019)

5.12 MECHANISMS AND ARROW PUSHING

(Timothy Soderberg, Organic Chemistry with a Biological Emphasis, 2016, 306-308, Text that referred to previous portions of Soderberg’s text are removed and marked with […] )

We'll begin with a relatively simple type of reaction that you are no doubt familiar with from previous chemistry classes: an acid-base reaction.

Here is the acid-base reaction between hydroxide and hydrochloric acid:

Note: A reaction such as the one above would of course include a spectator cation, such as sodium (Na+) or potassium (K+). In most of the reaction figures that we'll see throughout this book, the spectator ion is not shown in the interest of simplicity.

A proton is transferred from HCl, the acid, to hydroxide ion, the base. The product is water (the conjugate acid of hydroxide ion) and chloride ion (the conjugate base of HCl). Despite its simplicity (and despite the reactants and products being inorganic rather than organic), this reaction allows us to consider for the first time many of the fundamental ideas of organic chemistry that we will be exploring in various contexts […].

One very important key to understanding just about any reaction mechanism is the concept of electron density, and how it is connected to the electron movement (bond-breaking and bond-forming) that occurs in a reaction. The hydroxide ion – specifically, the oxygen atom bearing the negative formal charge – has high electron density: it is electron-rich.

Exercise 5.12.1 What is the LUMO in the reaction of hydroxide and hydrochloric acid?

The hydrogen atom in HCl, on the other hand, has low electron density: it is electron-poor, because chlorine is more electronegative than hydrogen. As you might expect, an atom that is electron-rich is likely to be attracted to an atom that is electron-poor. As hydroxide and HCl move closer to each other, a new bond forms between oxygen and hydrogen, and the hydrogen-chlorine bond breaks. The end result is a water molecule and a chloride anion.

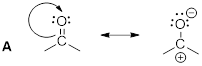
In organic chemistry terms, a reaction mechanism is a formalized description of how a reaction takes place -how we get, in other words, from reactants to products. Previously […], we saw how curved arrows were used to depict the ‘imaginary’ movement of two electrons when illustrating the conversion between two resonance contributors of the same molecule or ion (remember from that discussion that the conversion between two resonance contributors is not a reaction -it is merely an illustration of two different ways to draw the same molecule). The same curved arrow convention is used in mechanism drawings to show the electron movement that takes place in chemical reactions, where bonds are actually broken and formed. The mechanism for the HCl + OH^- reaction, for example, can be depicted by drawing two curved arrows.

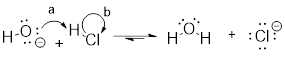
Arrow (a) in the mechanistic drawing originates at one of the lone pairs on the hydroxide oxygen and points to the ‘H’ symbol in hydrochloric acid, illustrating the ‘attack’ of the oxygen lone pair and subsequent formation of a new hydrogen-oxygen bond. Arrow (b) originates at the middle of hydrogen-chlorine bond and points to the ‘Cl’ symbol, indicating that this bond is breaking: the two electrons that make the bond are ‘leaving’ and becoming a lone pair on chloride ion.

When two (or more) curved arrows are drawn in the same figure of a mechanism, the intended meaning is that the electron movements being shown are occurring simultaneously. For example, in the figure above, the electron movement illustrated by arrow (a) (O-H bond formation) is occurring at the same time as the H-Cl bond breaking illustrated by arrow (b).

The transition state (TS) of a chemical step is a point at which bonds are in the process of breaking and/or forming. Transition states are illustrated by drawing the forming/breaking bonds as dotted lines and are enclosed by brackets with the 'double-dagger' symbol. For example, the transition state in the acid-base reaction between hydroxide and HCl can be illustrated as:

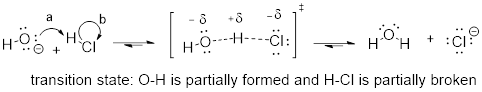
Notice in the drawing above that both the oxygen and the chlorine bear partial negative charges at the transition state: the formal charge on oxygen changes from -1 to 0 during this step of the reaction, while the formal charge on chlorine changes from 0 to -1.

While it can sometimes be instructive to include a transition state drawing in an organic mechanism diagram, they are not 'obligatory' elements of such a diagram. When asked to draw a reaction mechanism in the exercises and problems […], you need not include TS drawings in your answer unless specifically directed to do so.

5.13 ARROW PUSHING in SPECIFIC REACTIONS

(Ashley Jolly Steelman, 2019)

We will find that there are two ways that we can break a bond. In the acid-base reaction that we just examined, we moved a pair of electrons using a two headed arrow. This type of electron pushing is termed heterolytic bond cleavage. Typically, in this type of reaction we are forming ions.

We will find that in some reactions we will need to only move one electron at a time. This type of electron pushing is termed homolytic bond cleavage. To denote the movement of one electron at a time we will use a single-headed (fishhook) arrow instead of double-headed arrow. In this type of reaction, we will form radicals which is a molecule that contains at least one unpaired electron.

5.13.1 Heterolytic Bond Cleavage

Three typical patterns will arise as we start pushing electrons in mechanisms heterolytically.

1) Proton transfer: classified by the movement of a proton from one compound to another.

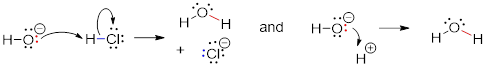
Note: Even though people represent the reaction above to the right with a naked proton (H⁺), there are no unbound protons. The proton is always passed from a species with electrons to another. Electrons can always benefit from interaction with another empty orbital. You were likely cautioned in General Chemistry to draw ⁺H₃O instead of ⁺H.

2) Nucleophilic attack: classified by a nucleophile attacking an electrophile. Place the tail of the arrow on the nucleophilic center and the head of the arrow on the electrophilic center.

Note: Remember that the species above is not ⁺CH₃; it is ⁺C(CH₃)₃. Methyl cation, like the proton, is too electrophilic to exist unbound. Like the proton, it can only be passed from the electrons of one molecule to those of another. We will unpack why later.

Notice how similar the proton transfer mechanism is to the nucleophilic attack. This is because the proton is a nucleus; the proton is an electrophilic nucleus like the C atom is in the two cases above.

3) Loss of a leaving group: classified by an atom or molecule departing from a molecule with a pair of electrons.

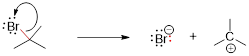
5.13.2 Homolytic Bond Cleavage

When breaking a covalent bond homolytically, each fragment will get one of the shared electrons. Notice that we are using single-headed arrows here because each arrow denotes the movement of one electron.

In the following chapters, we will be describing several different mechanisms in a stepwise fashion. It is important, when learning new mechanisms, to focus on the overall transformation of that process. Understanding, rather than memorizing, mechanisms is vital to learning organic chemistry.

5.13.3 Using Arrow Pushing in Mechanisms

It might help to note that all mechanisms in organic chemistry are just the combination of the four electron pushing patterns that we examined in the sub-sections above.

Example 1

Examine the reaction below and see if you can add electron pushing arrows for each step.

Solution

Step 1. This first step of the reaction is a proton transfer (simply an acid-base reaction). In our products to the right of the reaction arrow, the oxygen gained a proton (base) and the bromine lost its proton (acid). Recall that the tail of your arrow needs to start at a source of electron density and therefore, should start at the lone pair of electrons on the oxygen atom.

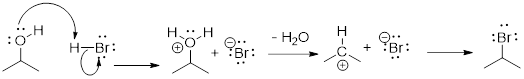
Step 2. The second step of the reaction shows the loss of a leaving group. The best leaving groups have low (often negative pKa values) for their corresponding conjugate acids (H₃O⁺, HBr, HCl etc.). When you see “–H₂O” over a reaction arrow, that means that water left as the leaving group. In our products to the right of the reaction arrow, the C now bears a positive formal charge because it has lost electrons.

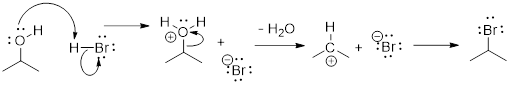
Step 3. The third step of the reaction is a nucleophilic attack. In order to determine the arrow pushing we need to decide which intermediate is our nucleophile vs. electrophile. In this case, bromine bears a negative charge clearly making it electron rich (nucleophile) and the carbocation can accept electron density (electrophile). Thinking about the arrow pushing, recall, nucleophiles attack electrophiles to decide where the tail of your arrow should begin.

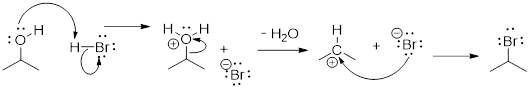
Next, see if you can work your way through these exercises.

Exercise 5.13.1 Draw the electron pushing curved arrows to show how electrons flow in the following transformations.

Exercise 5.13.2 Draw the electron pushing curved arrows to show how electrons flow in the following transformations.

Exercise 5.13.3 Draw the product(s) of the reaction mechanism indicated by the curved arrows drawn below.

(a)

(b)

Exercise 5.13.4 Draw in the electron pushing curved arrows needed for each step of the following radical mechanism.

KEY TO CHAPTER 5 EXERCISES

(Art Cammers, Ashley Jolly Steelman and Susan Odom 2019)

Exercise 5.4.1 Answer: E Bonds Broken −E Bonds Formed. 2(414) −436 −272 = 120 kJ /mol, endothermic.

Exercise 5.4.2 Answer: E Bonds Broken −E Bonds Formed. 400 +243 −349 −432 = −138 kJ /mol, exothermic.

Exercise 5.4.3 Answer: a) E Bonds Broken −E Bonds Formed. 2(347) −2(272) = 150 kJ /mol, endothermic. The reaction gives up two sigma bonds and makes two π bonds.

b) ΔS of this reaction is positive because two molecules have more ability to contain heat at lower temperature. There are two bodies that can move independently instead of one.

c) ) ΔG = ΔH – TΔS = is likely positive also since the enthalpy is so positive.

Exercise 5.4.4 Answer: a) ΔG_rxn > 0 will favor reactants, b) ΔG_rxn would be temperature dependent. c) ΔG_rxn will favor reactants at conditions specified.

Exercise 5.8.1 Answer: Exothermic vs. endothermic are state functions. Focus on the BDE difference between products an reactants ignore the path-based complexity in all this. You were also told to ignore light energy.

356 −366 −257 = -267 kJ /mol. Exothermic

If the reaction had to run without light.

192 +356 −366 −257 = -75 kJ /mol. Exothermic however a different reaction runs faster than this one in the absence of light. The reaction shown is usually kept cold to suppress the other reaction while it is irradiated.

Exercise 5.9.1 Answer: The best description would be (a) exergonic reaction (ΔG < 0) with bonds breaking and forming at the same time

Exercise 5.9.2 Answers:

(a) Which product is the thermodynamic product? P2

(b) Which product is the kinetic product? P1

(c) Would the two products be formed in an equal ratio (1:1) at equilibrium? Explain your reasoning. No P2 would dominate.

At equilibrium, we can consider R to be a reaction intermediate. Can you draw a reaction energy diagram that put R between P1 and P2? The ratio P2 /P1 = EXP((ΔGP1 – ΔGP2) /RT) from ΔGP2 – ΔGP1 = ΔG_rxn = −RT Ln Keq, Keq = P1 /P2, and ‑ΔG_rxn = ΔGP1 – ΔGP2.

Exercise 5.9.3 Answers: The forward reaction rate is unimolecular. The rate of the forward reaction in units of concentration per second (M /s) (rate_f = k_f[A‑B]) would decrease linearly as a function of decreasing concentration.

However, in the reverse bimolecular reaction, A and B have to collide; they have to find each other; (rate_r = k_r[A][B]). In the case in which A and B are in equal concentration (c) the rate of the reverse reaction would fall as function of c² as c decreases.

Since equilibrium is a ratio of competing rates, Keq = rate_f /rate_r = k_f[A‑B])/ k_r[A][B] = k_fc/ k_rc² = k_f /(k_r•c). So as c get smaller the equilibrium increases, favors the right side of the reaction as written.

Exercise 5.11.1 Answer: Add OH- and evaluate pKa.

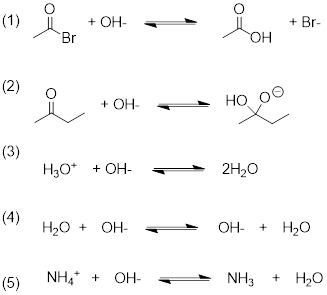
Look up the pKa of the conjugate acids of the base that is produced. We don’t have to worry about the pKa of the conjugate acid of the reactant. That is the same in each case. The pKa’s are as follows for (1) HBr = -9, (2) approx.13.5*, (3) H₃O⁺ = ‑1.7, (4) H₂O = 15.7, (5) NH₄⁺ = 9.3

* http://www.mch.estranky.sk/file/24/pka_tables.pdf search this document for hydrate. Used the value for acetaldehyde hydrate.

And the winner is (1) acetyl bromide is the most electrophilic.

Exercise 5.11.2 Answer: You are looking for electrons that are relatively high in energy. The two possibilities (and they are not that good) are CH₃Cl and H₂O because they have atomic lone pairs. The rest of the electrons are bound. Cl is electronegative and it is bound to CH₃. The lone pairs of electrons on the Cl atom in methyl chloride will not be available to donate to an electrophile.

H₂O can and does serve as a nucleophile; although, it is quite weak.

Exercise 5.11.3 Answer: In the following reaction, label the nucleophile and electrophile on the reactant side of the equation.

How do you know? Look at the product? Which molecule got the nucleus in the product? Which molecule gave up the nucleus in the product? The 3-C atom chain starts out neutral with six H atoms and ends up charged with seven H atoms in the product.

Exercise 5.11.4 Answer: The occupied AOs of chloride are lower in energy than the unoccupied AOs of Na⁺. The bond does not form because the σ bonded pair of electrons would be higher in energy than the lone pair on the chloride. This is the plain vanilla recipe for ionic bonds.

Exercise 5.11.5 Answer: Try to look up the BDE of the CC bond formed and compare the pKa of the conjugate acids of the anions in reactant and product. See the section entitled pKa is a unit of energy.

Exercise 5.12.1 Answer: the σ* orbital in HCl

Exercise 5.13.1 Answer:

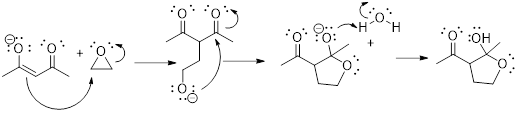
Exercise 5.13.2 Answer:

Exercise 5.13.3 Answer:

(a)

(b)

Exercise 5.13.4 Answer:

It's a good idea to show the H atoms you will be working with explicitly

Redrawing and only showing mechanism from left to right is OK. It

allows you to reset your thinking.We want Cl atom from the most

available source. The Cl2 molecule. It is a good idea to draw this

out with the s bond.

CHAPTER 5 PRACTICE PROBLEMS

(Ashley Jolly Steelman, 2019)

PP 5-01 Consider the reaction coordinate diagram and answer the following questions.

a) Is the reaction endergonic or exergonic?

b) The reaction has ________ intermediates.

c) The reaction has ________ steps.

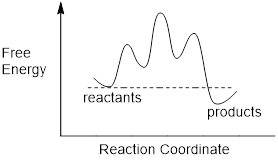
PP 5-02 Which of the descriptions (A to D) correctly describe the following energy diagram?

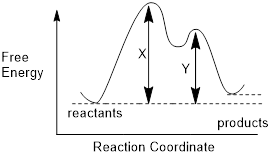
a) a two-step exothermic reaction having an activation energy = X

b) a two-step endothermic reaction having an activation energy = X

c) a two-step endothermic reaction having an activation energy = Y

d) a two-step exothermic reaction having an activation energy = Y

PP 5-03 Determine whether or not equilibrium will favor the reactants or products based on the following information: an endothermic reaction for which the system exhibits a increses in entropy.

PP 5-04 Which of the following molecules cannot serve as an electrophile?

PP 5-05 For each of the following reactions determine ∆S for the reaction (∆S_sys). Will ∆S be positive, negative or approximately zero.

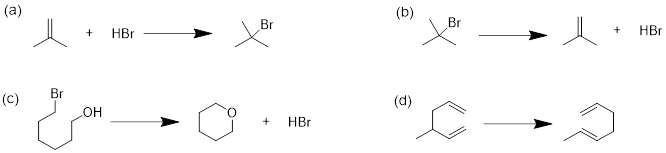
PP 5-06 Draw in the curved arrows for each of the following reactions.

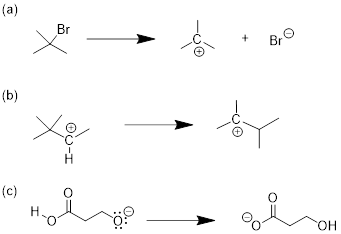
PP 5-07 Draw in the curved arrows for each step of the following reaction mechanism.

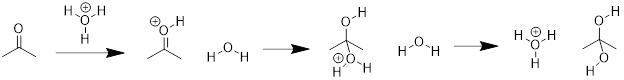
PP 5-08 Answer the following questions about the energy diagram.

(a) Which letter represents the activation energy for the forward reaction?

(b) Is the forward reaction endothermic or exothermic?

(c) Addition of a catalyst would lower the ___________________.

(d) (True/False) Addition of a catalyst will change the value for ΔH.

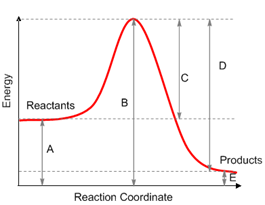
KEY TO CHAPTER 5 PRACTICE PROBLEMS

PP 5-01 Answer:

a) Is the reaction endergonic or exergonic? exergonic

b) The reaction has ________ intermediates. Two

c) The reaction has ________ steps. Three steps, each elemental step has a transition state.

PP 5-02 Answer:

a) a two-step exothermic reaction having an activation free energy = X

b) a two-step endothermic reaction having an activation free energy = X

c) a two-step endothermic reaction having an activation free energy = Y

d) a two-step exothermic reaction having an activation free energy = Y

PP 5-03 Answer: ∆G_rxn may be temperature dependent.

PP 5-04 Answer: NaOH

PP 5-05 Answer: a) ∆S_sys is expected to be negative. Two moles of reactant are converted into one mole of product. b) ∆S_sys is expected to be positive. One mole of reactant is converted into two moles of product. c) ∆S_sys is expected to be positive. One mole of reactant is converted into two moles of product. d) ∆S_sys is expected to be approximately zero. One mole of reactant is converted into one mole of product and both reactant and product are acyclic.

PP 5-06 Answer:

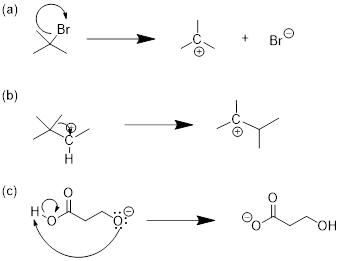
PP 5-07 Answer:

PP 5-08 Answer:

(a) C

(b) Exothermic

(c) Activation energy

(d) False